Моделирование фазовых равновесий при кристаллизации базальтовых магм
|
Условные обозначения |
Авторы: А.А.Арискин, Г.С.Бармина
Лаборатория термодинамики и математического моделирования природных процессов ГЕОХИ РАН
(Моделирование фазовых равновесий при кристаллизации базальтовых магм.-М.:Наука,МАИК "Наука/Интерпериодика",2000.-363с.) |
Назад | Оглавление| Далее
Выше отмечалось, что в качестве примера применимости фракционной кристаллизации Боуэн (1934) привел результаты генетической интерпретации базальтовых ассоциаций Малла (Гебридские о-ва), входяших в состав Британо-Арктической провинции (Baily et al., 1924). Авторы труда о породах Малла выделили 2 главных типа базальтов, так называемый "тип плато" с содержанием ~ 45 вес.% SiO2, 8% MgO и около 3% Na2O+K2O и базальты "центрального непорфирового типа", содержащие 50 вес.% SiO2, 5% MgO и ~ 4% суммы щелочей. Позднее эти типы были определены как оливиновые и толеитовые базальты (Kennedy, 1933; Шейнманн, 1968).
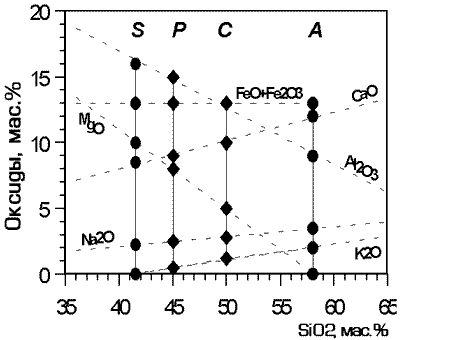
Вопрос о возможной генетической связи между этими породами конкретизировал Боуэн. Он высказал предположение, что родоначальной магмой является более основная оливин-базальтовая и сформулировал проблему следующим образом: чтобы преобразовать оливин-базальтовую магму в относительно богатую кремнеземом толеитовую, необходимо путем ассимиляции добавить некоторое количество обогащенного SiO2 компонента, либо путем кристаллизации вычесть компонент, обедненный SiO2 (Боуэн, 1934). Для оценки составов этих возможных компонентов было предложено использовать диаграммы добавления-вычитания (Рис. 1.2).
|
|
|
Рис. 1.2. Диаграмма добавления -вычитания для магм "типа плато" (P) и "центрального непорфирового типа" Мулля (C) - Боуэн (1934)
Cостав S соответствует вычитаемому компоненту, который можно представить как смесь Pl, Ol, Cpx, и Mt
|
В итоге было показано, что в случае ассимиляции к оливин-базальтовой магме необходимо добавить от 25 до 62% кислого вещества, содержащего 70-58% SiO2 и весьма экзотичные для данной провинции концентрации Al2O3, FeO, CaO и щелочей. В случае кристаллизационной гипотезы, рассчитанный валовый состав вычитаемого компонента оказался идентичен смеси кристаллов плагиоклаза, оливина, клинопироксена и магнетита (в пропорции примерно 52:27:7:4). Эти минеральные фазы реально представлены в породах "типа плато" и по петрографическим данным были отнесены к фазам ранней кристаллизации (Baily et al., 1924). Полученные данные позволили сделать вывод, что "переход одной магмы в другую был результатом выпадения кристаллов плагиоклаза и оливина", а наблюдамое в толеитовых базальтах накопление кремнезема отражает реакционные отношения оливина с магматическим расплавом.
Мы остановились на данном примере по той причине, что фактически это была первая попытка в петрологии оценить результаты фракционирования базальтовой магмы, используя способ вычитания из системы твердых фаз. В соответствии с современной терминологией этот подход следовало бы отнести к методам решения обратных задач геохимических процессов: ведь сначала Боуэн использовал метод баланса масс для оценки валового химического состава вычитаемого (кристаллизующегося) компонента, а затем пересчитал его на пропорции реально существующих минералов.
В последующие годы более широкое распространение получил метод прямого расчета фракционной кристаллизации с использованием заданного набора и состава минеральных фаз (Wright, Doherty, 1970; Поляков, Муравьева, 1981). В основе этого подхода лежит решение систем линейных уравнений баланса масс для выбранного ряда химических элементов (i - петрогенный оксид или микроэлемент) и кристаллизующихся минералов (1=< j<= m):
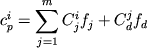 , (1.1) , (1.1)
где 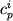 - предполагаемый состав исходного расплава (для этого выбирается относительно "примитивный" образец); - предполагаемый состав исходного расплава (для этого выбирается относительно "примитивный" образец); 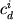 - предполагаемый состав дифференциата, т.е. породы или расплава, которые могут являться продуктом фракционирования заданного источника; - предполагаемый состав дифференциата, т.е. породы или расплава, которые могут являться продуктом фракционирования заданного источника; 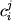 и и 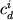 - содержание i-го элемента в j -минерале и дифференциате; - содержание i-го элемента в j -минерале и дифференциате; 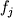 и и 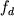 - искомые пропорции кристаллизующихся минералов и образованного дифференциата (мас.%). - искомые пропорции кристаллизующихся минералов и образованного дифференциата (мас.%).
Показателем качества проведенных расчетов являются положительные значения 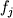 > 0, близость суммарного количества фаз к единице > 0, близость суммарного количества фаз к единице 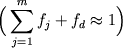 и значения невязок для каждого элемента и значения невязок для каждого элемента 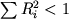 , которые определяются по разности между заданным и рассчитанным по модели составом исходного расплава. Выполнение перечисленных условий обычно рассматривается в качестве доказательства справедливости гипотезы фракционирования (Wright, Doherty, 1970). , которые определяются по разности между заданным и рассчитанным по модели составом исходного расплава. Выполнение перечисленных условий обычно рассматривается в качестве доказательства справедливости гипотезы фракционирования (Wright, Doherty, 1970).
|
|
|
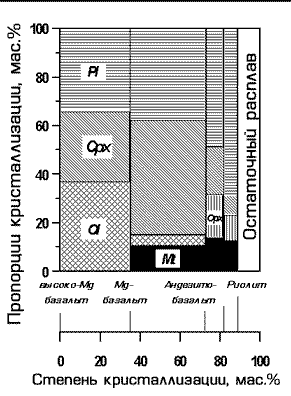
Рис. 1.3. Рассчитанный состав кристаллизующегося материала на интервалах фракционирования исходной высокомагнезиальной магмы толеитовых серий Исландии
По данным работы (Поляков, Муравьева, 1981)
|
Подобные расчеты сыграли важную роль в развитии представлений о фракционировании базальтовых магм и в определенном смысле явились прототипом других эмпирических моделей фракционной кристаллизации, которые развивались в конце 70-х - первой половине 80-х годов (Drake, 1976a; Longhi, 1977; Nathan, Vankirk, 1978; French, Cameron,1981;Арискин, Френкель, 1982; Petitpierre, Boivin, 1983). Вместе с тем, нельзя не отметить очевидный недостаток моделей фракционирования, построенных по методу наименьших квадратов. Решение систем уравнений баланса масс является здесь формальной математической процедурой, которая не гарантирует соответствия рассчитанных пропорций и составов экспериментальным данным по фазовым равновесиям. По этой причине приходится допускать постоянство состава минералов и пропорций кристаллизации на достаточно широких интервалах фракционирования (обычно при таком подходе весь ряд дифферециации разбивается на 4-5 шагов - Рис. 1.3).
Понятно, что при наличии таких допущений петрологам далеко не всегда удается сделать однозначный вывод о реальности или нереальности процесса фракционирования магмы, исходя из невязок решения задачи по отдельным элементам. В качестве иллюстрации этого недостатка простых масс-балансовых методов можно привести финал истории с боуэновской интерпретацией генетических соотношений базальтоидов Малла (Рис. 1.2). Последующая трактовка оливиновых и толеитовых базальтов, основанная на результатах более детального геохимического изучения, предполагает, что первые дают начало не толеитовой, а щелочной серии пород, крайние члены которой представлены муджиеритами (Kennedy, 1933; Шейнманн, 1968).
Таким образом, для построения более реалистичных моделей фракционной кристаллизации базальтовых магм, системы массбалансовых уравнений типа источник-дифференциат (1.1) необходимо совместить с данными по равновесиям минерал-расплав, которые бы однозначно связывали состав силикатной жидкости с составом твердой фазы на каждом интервале фракционирования. Подходы к построению такого рода вычислительных схем будут даны в разделе, посвященном численным методам. Но сначала рассмотрим важнейшие следствия некоторых аналитических моделей фракционирования для простых силикатных систем.
Процессы фракционирования расплавов в общем виде описываются при помощи обыкновенных дифференциальных уравнений, основанных на балансе масс, напр. (Greenland, 1970; Maaloe, 1976). Основное условие баланса количества i-го компонента в расплаве и твердой фазе при кристаллизации имеет вид
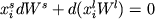 , (1.2) , (1.2)
где 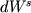 - приращение массы или количества молей кристаллов, - приращение массы или количества молей кристаллов, 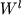 - количество расплава, - количество расплава, 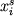 и и 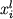 - концентрации i-го компонента в твердой фазе (s) и жидкости (l). Для целей дальнейшего описания удобно воспользоваться параметром, который называется степенью фракционирования расплава и характеризует отношение общей массы кристаллизовавшегося вещества - концентрации i-го компонента в твердой фазе (s) и жидкости (l). Для целей дальнейшего описания удобно воспользоваться параметром, который называется степенью фракционирования расплава и характеризует отношение общей массы кристаллизовавшегося вещества 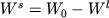 к количеству исходного расплава к количеству исходного расплава 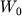 (Кравченко, 1977): (Кравченко, 1977):
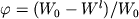 , (1.3) , (1.3)
Условия вида (1.2,1.3) дают систему из n дифференциальных уравнений (1 =< i =< n):
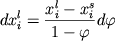 , (1.4) , (1.4)
которые однозначно связывают эволюцию состава расплава 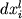 и степень протекания процесса фракционной кристаллизации. и степень протекания процесса фракционной кристаллизации.
Решать эту систему аналитически удается только в простейших случаях, когда известны дополнительные зависимости между составом расплава и твердой фазы.
Фракционирование микроэлементов. Например, можно принять, что на любой стадии фракционирования выполняются условия:
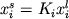 , , 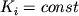 ( 1.5) ( 1.5)
где 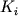 - средневзвешенный или комбинированный (Рябчиков, 1965) коэффициент распределения i-го элемента между твердой фазой и расплавом: - средневзвешенный или комбинированный (Рябчиков, 1965) коэффициент распределения i-го элемента между твердой фазой и расплавом:
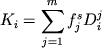 , (1.6) , (1.6)
где 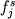 - весовая доля фазы j в кристаллизующемся материале3 , - весовая доля фазы j в кристаллизующемся материале3 , 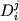 - индивидуальный коэффициент распределения i-го элемента между j - минералом и расплавом. Соотношения (1.4-1.5) дают известную формулу Релея-Макфи - индивидуальный коэффициент распределения i-го элемента между j - минералом и расплавом. Соотношения (1.4-1.5) дают известную формулу Релея-Макфи
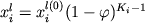 , (1.7) , (1.7)
где 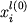 - концентрация i-го элемента в исходном расплаве. - концентрация i-го элемента в исходном расплаве.
Уравнение (1.7) описывает случай так называемой идеальной (perfect - Maaloe, 1976) фракционной кристаллизации и широко использовалось для анализа поведения и оценок эффективных коэффициентов разделения микроэлементов в магматическом процессе (McIntire, 1963; Рябчиков, 1965; Gast, 1968; Greenland, 1970; Кравченко, 1977 и многие другие). Для идеального фракционирования характерно 100% удаление кристаллизующегося материала из расплава при условии, что количество фракционирующего расплава на каждой стадии комплементарно количеству выделившихся кристаллов 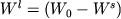 . .
Неидеальная или частичная (partial) фракционная кристаллизация также предполагает полное удаление кристаллического вещества, однако при этом допускается, что часть жидкости может быть удалена из основного объема фракционирующего расплава, например в виде межкристаллического материала (Maaloe, 1976). Это приводит к эффективному уменьшению общего количества фракционирующей жидкости не только за счет кристаллизации, но также удаления из системы "захваченного кристаллами расплава". Основное условие баланса (1.2) при этом приобретает вид
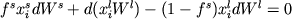 , (1.8) , (1.8)
где 0 =< 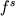 =< 1 - фактор фракционирования, равный доле твердых фаз от общего количества вещества, удаленного из расплава на заданном интервале кристаллизации. Уравнение Рэлея-Макфи (1.7) с учетом этого фактора преобразуется к виду =< 1 - фактор фракционирования, равный доле твердых фаз от общего количества вещества, удаленного из расплава на заданном интервале кристаллизации. Уравнение Рэлея-Макфи (1.7) с учетом этого фактора преобразуется к виду
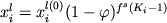 . (1.9) . (1.9)
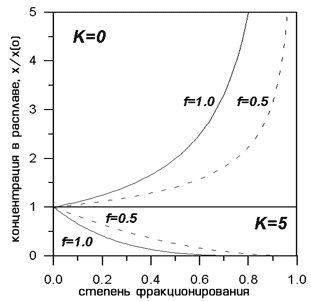
На Рис. 1.4 показаны зависимости, рассчитанные при помощи уравнения (1.9) для случаев идеальной и частичной фракционной кристаллизации. Фактор фракционирования во втором случае равнялся 0.5, что отвечает удалению из фракционирующей системы твердых фаз и расплава в отношении 1:1. При расчетах использовалось два значения комбинированного коэффициента распределения: K=0 (модель несовместимого или некогерентного элемента) и K=5 (модель элемента, предпочтительно распределяющегося в твердую фазу).
|
|
|
Рис. 1.4. Эволюция состава расплава для случаев идеальной (f=1.0) и частичной (f=0.5) фракционной кристаллизации
Расчеты моделируют поведение сильно несовместимого (K=0) и совместимого с твердой фазой (K=5) элемента. Концентрации нормализованы на исходное содержание элемента в расплаве x(o)
|
Данные Рис. 1.4 показывают, что при идеальной фракционной кристаллизации быстрое обогащение жидкости несовместимым элементом и обеднение совместимым элементом происходит с начальных стадий фракционирования. При частичной фракционной кристаллизации эти процессы замедляются, поскольку эффективность разделения элементов буферируется количеством и составом захваченного расплава. Рассмотренные здесь случаи представляют петрологический интерес, поскольку полное разделение кристаллов и фракционирующего расплава в природных условиях маловероятно из физических соображений. Хорошо известны прямые доказательства захвата магматического расплава в кумулятивных породах - так называемый интеркумулятивный материал (Уэйджер, Браун, 1970). О реальности такого рода процессов свидетельствуют результаты численного моделирования внутрикамерной дифференциации трапповых магм и решения обратных геохимических задач (Френкель и др., 1988). В работе мы будем неоднократно возвращаться к этим вопросам. Рассмотрим важнейшие петрогенетические следствия зависимостей, приведенных на Рис. 1.4.
- (1) Характерная особенность рассчитанных эволюционных линий состоит в том, что в случае идеальной фракционной кристаллизации количество остаточного расплава с высоким содержанием некогерентного элемента x/x(o) > 5 в 4-5 раз превышает количество аналогичного дифференциата, полученного при условии захвата 50% жидкости. Этот результат является прямым следствием прогрессивного уменьшения количества фракционирующего расплава, которое усиливается при увеличении доли захваченной кристаллами жидкости.
Таким образом приходим к выводу, что в зависимости от условий протекания или динамики фракционирования (см. ниже)один и тот же исходный расплав может генерировать крайние дифференциаты, имеющие близкий состав, но количество которых может отличаться на порядок относительно массы исходного расплава. Понимание природы этих соотношений заставляет с осторожностью относиться к петрологическим интерпретациям масс-балансовых расчетов, включающих прямое перенесение данных физических или численных экспериментов по плавлению пород на конкретные магматические объекты. Эти вопросы мы рассмотрим на примере моделирования фазовых равновесий и внутрикамерной дифференциации исходных магм комплекса изверженных пород Садбери (Онтарио, Канада) - см. Главу 6.
- (2) Другой важный момент касается формы зависимости концентрационной кривой от степени фракционирования. Как видно из Рис. 1.4, при частичной фракционной кристаллизации отмечается значительно более резкий переход к стадии сильного обогащения расплава некогерентным элементом. Если экстраполировать подобные зависимости на природные системы, фракционирующие по главным компонентам (в частности, SiO2), то можно ожидать, что при прочих равных условиях захват расплава будет способствовать усилению бимодальности в распределении основных и кислых продуктов кристаллизационной дифференциации, которая, как полагают (Луканин, 1985), является следствием резкого перегиба петрохимических трендов при появлении на ликвидусе магнетита - Рис. 1.1.
- (3) Несмотря на то, что основные закономерности фракционирования элементов в условиях захвата/удаления кристаллов и расплава были описаны еще в 70-е годы (Greenland, 1970; Maaloe, 1976) и смоделированы в начале 80-х (Френкель, 1982), концепция идеальной фракционной кристаллизации получила преобладающее распространение среди петрологов. Зависимости типа (1.7) использовались не только для моделирования прямого хода фракционной кристаллизации, но также обратных задач, связанных с оценкой эффективных коэффициентов разделения микроэлементов по геохимическим данным (Кравченко, 1977). Анализ уравнения (1.9) свидетельствует, что без учета фактора фракционирования
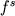 подобный подход может приводить к оценкам подобный подход может приводить к оценкам 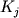 , которые в 1.5-2.5 отличаются от реальных значений. С другой стороны, при наличии надежных экспериментальных данных по коэффициентам распределения минерал-расплав соотношения типа (1.9) позволяют проводить оценки усредненного фактора фракционирования (плотности кумулуса), характерного для внутрикамерной дифференциации основных магм (Бармина и др., 1982). , которые в 1.5-2.5 отличаются от реальных значений. С другой стороны, при наличии надежных экспериментальных данных по коэффициентам распределения минерал-расплав соотношения типа (1.9) позволяют проводить оценки усредненного фактора фракционирования (плотности кумулуса), характерного для внутрикамерной дифференциации основных магм (Бармина и др., 1982).
В завершение заметим, что понятие частичной фракционной кристаллизации не следует отождествлять с промежуточным (intermediate) фракционированием. Дело в том, что в природных системах удаление кристаллов из фракционирующей жидкости может проходить не полностью, так что часть кристаллов остается в виде фазы, взвешенной в основном объеме магмы. При этом не весь кристаллический материал исключается из равновесия с расплавом, а фракционирование приобретает характер промежуточного между процессами фракционной и равновесной кристаллизации.
Фракционирование минералов-твердых растворов.
Многие исследователи подчеркивали ограниченные возможности использования уравнений типа (1.4-1.7) для построения и исследования моделей фракционирования главных элементов, прежде всего из-за широких вариаций значений индивидуальных ( 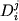 ) и средневзвешенных ( ) и средневзвешенных ( 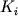 ) коэффициентов распределения петрогенных оксидов. Эти вариации могут носить монотонный характер (например вследствие зависимости ) коэффициентов распределения петрогенных оксидов. Эти вариации могут носить монотонный характер (например вследствие зависимости 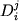 и и 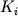 от состава и/или температуры), но главные трудности связаны со скачкообразными изменениями этих параметров при изменении фазового состава кристаллизующихся ассоциаций. Другая проблема касается эволюции пропорций кристаллизации от состава и/или температуры), но главные трудности связаны со скачкообразными изменениями этих параметров при изменении фазового состава кристаллизующихся ассоциаций. Другая проблема касается эволюции пропорций кристаллизации 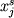 даже при постоянстве набора кристаллизующихся фаз - см. уравнение (1.6). Эта информация в явном или неявном виде представлена в фазовых диаграммах силикатных систем. даже при постоянстве набора кристаллизующихся фаз - см. уравнение (1.6). Эта информация в явном или неявном виде представлена в фазовых диаграммах силикатных систем.
Обратимся сначала к простой бинарной системе Fa-Fo (Bowen, Schairer, 1935). Здесь может кристаллизоваться только один минерал - оливин, что позволяет при аналитическом описании его фракционирования избежать влияния факторов порядка и пропорций кристаллизации. Эволюцию состава оливина удобно описать при помощи коэффициента сокристаллизации 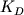 : :
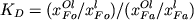 , (1.10) , (1.10)
который связывает состав твердой фазы (Ol) и расплава. Решение уравнения (1.4) с учетом (1.10) и условий баланса 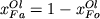 и и 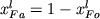 дает выражение (Арискин, Френкель, 1982): дает выражение (Арискин, Френкель, 1982):
![$x_{Fo}^{l} / (1-x_{Fo}^{l} )^{K_D} = [x_{Fo}^{l(0)}/(1 - x_{Fo}^{l(0)})^{K_D}] (1- \varphi)^{K_D-1}$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula611.gif) , (1.11) , (1.11)
где 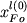 - исходное содержание Fo в расплаве при - исходное содержание Fo в расплаве при 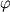 = 0. Это нелинейное уравнение легко решается относительно = 0. Это нелинейное уравнение легко решается относительно 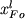 итерационными методами. Состав расплава при данной степени фракционирования итерационными методами. Состав расплава при данной степени фракционирования 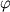 определяет состав кристаллизующегося оливина: определяет состав кристаллизующегося оливина:
![$x_{Fo}^{Ol} = K_D X_{Fo}^l / [ 1 + ( K_D - 1 ) X_{Fo}^l]$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula616.gif) . (1.12) . (1.12)
|
|
|
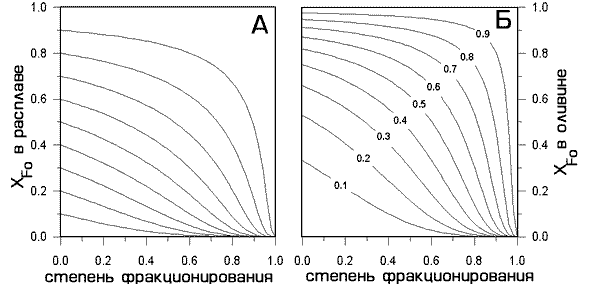
Рис. 1.5. Эволюция состава расплава и оливина при идеальном фракционировании в бинарной системе Fa-Fo
А Состав расплава, Б Состав оливина (цифры у линий отвечают содержанию Fo в исходной жидкости). Расчеты проведены по уравнениям (1.11, 1.12) для KD = 4.5.
|
Рассчитанные зависимости содержания Fo в расплаве и оливине от степени фракционирования в бинарной системе Fa-Fo показаны На Рис. 1.5. При проведении этих расчетов использовалось среднее значение KD = 4.5, поскольку экспериментальные данные по системе Fa-Fo (Bowen, Schairer, 1935) указывают, что величина коэффициента сокристаллизации варьирует здесь в пределах 4.1-5.2 (Bradley, 1962).
Главная особенность этих эволюционных линий - отчетливая зависимость скорости изменения состава расплава и оливина 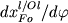 от начального содержания Fo в силикатной жидкости. Чем выше содержания Fo в исходном расплаве, тем медленнее изменяются составы фаз на начальных стадиях фракционирования и быстрее на конечных. И, наоборот, расплавы с промежуточными и низкими исходными содержаниями Fo фракционируют быстрее на начальных стадиях кристаллизации. Аналогичные соотношения наблюдались в системе Ab-An, где скорость изменения состава фракционирующего расплава и плагиоклаза оказалась зависимой от исходного содержания анортитового компонента (Maaloe, 1976). Это позволяет предполагать, что установленная зависимость носит общий характер: скорость фракционирования (измененения состава) силикатных систем определяется нормативным соотношением в исходном расплаве тугоплавких и легкоплавких миналов (Арискин, Френкель, 1982). от начального содержания Fo в силикатной жидкости. Чем выше содержания Fo в исходном расплаве, тем медленнее изменяются составы фаз на начальных стадиях фракционирования и быстрее на конечных. И, наоборот, расплавы с промежуточными и низкими исходными содержаниями Fo фракционируют быстрее на начальных стадиях кристаллизации. Аналогичные соотношения наблюдались в системе Ab-An, где скорость изменения состава фракционирующего расплава и плагиоклаза оказалась зависимой от исходного содержания анортитового компонента (Maaloe, 1976). Это позволяет предполагать, что установленная зависимость носит общий характер: скорость фракционирования (измененения состава) силикатных систем определяется нормативным соотношением в исходном расплаве тугоплавких и легкоплавких миналов (Арискин, Френкель, 1982).
Если экстраполировать эти зависимости на реальные многокомпонентные силикатные расплавы, то можно сделать вывод, что для магнезиальных систем с высокими отношениями MGN=MgO/(FeO+MgO) следует ожидать относительно медленное понижение магнезиальности MGN в начале фракционирования фемических минералов (0 < 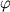 < 20-40%), умеренное на средних стадиях (0 < < 20-40%), умеренное на средних стадиях (0 < 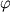 < 40-70%) и резкое обеднение составов магнием (вплоть до образования "чисто железистых" минералов) на заключительных стадиях процесса. При кристаллизации плагиоклаза или Pl-содержащих ассоциаций скорость фракционирования системы по CaO, Na2O, Al2O3 и SiO2 будет изменяться в зависимости от щелочности. < 40-70%) и резкое обеднение составов магнием (вплоть до образования "чисто железистых" минералов) на заключительных стадиях процесса. При кристаллизации плагиоклаза или Pl-содержащих ассоциаций скорость фракционирования системы по CaO, Na2O, Al2O3 и SiO2 будет изменяться в зависимости от щелочности.
Полезную информацию об особенностях фракционирования бинарных систем дает также сравнение эволюционных линий на Рис. 1.5А и 1.5Б. В силу того, что относительно расплава твердая фаза обогащена тугоплавким компонентом, изменение состава минерала (Рис. 1.5Б) происходит менее резко, чем изменение состава расплава (Рис. 1.5А). Именно по этой причине незначительным вариациям состава оливина в природных объектах (на уровне первых мол.%) могут отвечать весьма существенные изменения состава магматического расплава - см. например данные по составам расплавных включений в оливинах (Соболев, 1996).
Попытки аналитического решения проблемы фракционирования в многокомпонентных силикатных системах исчерпываются анализом тройных диаграмм, в частности Ab-An-Di (Maaloe, 1976). При этом совмещается решение двух задач: необходимости отслеживать изменение состава Pl и изменение в процессе фракционирования пропорций кристаллизации плагиоклаза и пироксена. Для решения этих задач используются данные о конфигурации фазовых полей, представленные в виде полиномов, аппроксимирующих соотношения между экспериментальными значениями 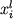 и и 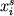 : эти соотношения подставляются в уравнения вида (1.4). Такие модели представляют скорее теоретический интерес и могут быть применимы только для систем, где положение фазовых границ в зависимости от состава полностью охарактеризовано на некотором предварительном этапе. Заметим, что в рамках подобных подходов сложно учесть реакционные соотношения между фазами, которые приводят к изгибу пути фракционирования состава расплава за счет ухода с перитектических линий в область кристаллизации нового минерала. : эти соотношения подставляются в уравнения вида (1.4). Такие модели представляют скорее теоретический интерес и могут быть применимы только для систем, где положение фазовых границ в зависимости от состава полностью охарактеризовано на некотором предварительном этапе. Заметим, что в рамках подобных подходов сложно учесть реакционные соотношения между фазами, которые приводят к изгибу пути фракционирования состава расплава за счет ухода с перитектических линий в область кристаллизации нового минерала.
Численные схемы фракционирования
Существо численных методов расчета траекторий фракционной кристаллизации сводится к замене в уравнениях вида (1.4) бесконечно малых приращений d конечными 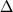 : :
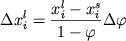 , (1.13) , (1.13)
откуда после каждого k-шага кристаллизации
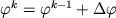 , (1.14) , (1.14)
а состав расплава
![$x_i^{l(k)} = x_i^{l(k-1)} + [ x_i^{l(k-1)} - x_i^{s(k-1)} ] \Delta \varphi / (1 - \varphi^{k-1})$](http://images.geo.web.ru/pubd/2002/10/26/0001164692/tex/formula625.gif) . (1.15) . (1.15)
Эта конечно-разностная схема гарантирует высокую математическую точность построения траекторий фракционной кристаллизации при заданных малых приращениях 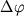 (0.1-0.01% и меньше). Реалистичность рассчитанных эволюционных линий зависит от того, насколько корректно предсказываются зависимости между (0.1-0.01% и меньше). Реалистичность рассчитанных эволюционных линий зависит от того, насколько корректно предсказываются зависимости между 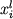 и и 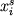 на каждой стадии фракционирования. Эти соотношения определяются: (1) фазовым составом ликвидусной ассоциации, (2) пропорциями кристаллизации минералов и (3) составами кристаллизующихся фаз. В 70-х годах было предложено несколько подходов к решению этих проблем (Drake, 1976a; Longhi, 1977; Nathan, Vankirk, 1978) - наиболее универсальной и последовательной с термодинамической точки зрения явилась модель кристаллизации, разработанная Натаном и Ванкирком. на каждой стадии фракционирования. Эти соотношения определяются: (1) фазовым составом ликвидусной ассоциации, (2) пропорциями кристаллизации минералов и (3) составами кристаллизующихся фаз. В 70-х годах было предложено несколько подходов к решению этих проблем (Drake, 1976a; Longhi, 1977; Nathan, Vankirk, 1978) - наиболее универсальной и последовательной с термодинамической точки зрения явилась модель кристаллизации, разработанная Натаном и Ванкирком.
Эти исследователи пошли по пути обобщения экспериментального материала по фазовым равновесиям синтетических и природных силикатных систем, который был накоплен за предыдущие 60 лет. Они справедливо отмечали, что достижения экспериментальной петрологии до сих пор были представлены в виде отрывочных данных, полученных в многомерном пространстве составов магматических пород для ограниченного диапазона температур и давлений. Задача состояла в том, чтобы найти способ согласования и интерполяции результатов разнообразных экспериментов по плавлению пород и синтетических смесей.
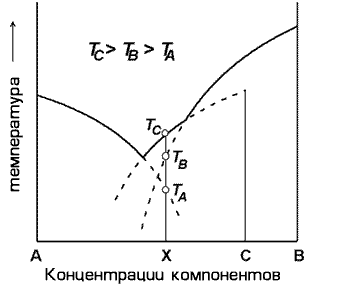
Для решения проблемы определения ликвидусных фаз, которые должны кристаллизоваться из расплава заданного состава, был предложен алгоритм, основанный на общих особенностях топологии фазовых диаграмм силикатных систем (Nathan, Vankirk, 1978). Принцип метода иллюстрирует схематичная диаграмма, показанная на Рис. 1.6. Эта диаграмма дает пример бинарной системы A-B с эвтектикой и перитектической точкой (типа системы SiO2-Mg2SiO4), где в дополнение к "минеральным" фазам A и B может кристаллизоваться фаза С, находящаяся с фазой B в реакционных соотношениях.
|
|
| Рис. 1.6. Схема возможных соотношений между ликвидусными и псевдоликвидусными температурами минералов в двойной системе с перитектической и эвтектической точками |
Как видно из этого рисунка, температура равновесия с расплавом для каждой из трех возможных в данной системе "минеральных" фаз описывается линией ликвидуса 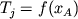 , которая определена на всем пространстве составов. Это означает, что при заданном составе X (см. Рис. 1.6) в "равновесии" с расплавом потенциально может находиться любой из трех "минералов", но только при определенной для каждого "псевдоликвидусной" (Арискин, Френкель, 1982) температуре. В действительности ликвидусным оказывается тот минерал, у которого температура нахождения на ликвидусе максимальна, в нашем случае - минерал С (Рис. 1.6). Таким образом, расчет набора и сравнение псевдоликвидусных температур потенциально возможных твердых фаз обеспечивает процедуру выбора минерала, который должен кристаллизоваться из расплава заданного состава. , которая определена на всем пространстве составов. Это означает, что при заданном составе X (см. Рис. 1.6) в "равновесии" с расплавом потенциально может находиться любой из трех "минералов", но только при определенной для каждого "псевдоликвидусной" (Арискин, Френкель, 1982) температуре. В действительности ликвидусным оказывается тот минерал, у которого температура нахождения на ликвидусе максимальна, в нашем случае - минерал С (Рис. 1.6). Таким образом, расчет набора и сравнение псевдоликвидусных температур потенциально возможных твердых фаз обеспечивает процедуру выбора минерала, который должен кристаллизоваться из расплава заданного состава.
Строгих доказательств правомерности предложенного подхода первоначально представлено не было (Nathan, Vankirk, 1978): термодинамический смысл этих соотношений стал ясен позднее (Френкель, Арискин, 1984). Дело в том, что из трех возможных "равновесных состояний" гетерогенной системы (расплав состава X + бесконечно малое количество твердой фазы A, B или C - Рис. 1.6) энергетически выгодным оказывается только одно, отвечающее максимально возможной температуре ликвидуса. Термодинамическое обоснование этого утверждения применительно к многокомпонентным расплавно-кристаллическим системам будет рассмотрено в Главе 2. Представляется важным, что данный подход может быть распространен и на котектические ассоциации, условие кристаллизации которых при построении численных моделей фракционирования приобретает вид:
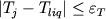 , , 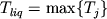 , , 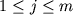 , (1.16) , (1.16)
где 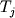 - псевдоликвидусная температура j - минеральной фазы, - псевдоликвидусная температура j - минеральной фазы, 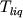 - ликвидусная температура расплава, - ликвидусная температура расплава, 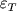 - заданная точность по температуре. Соотношения (1.16) по существу определяют точку пересечения ликвидусных поверхностей различных фаз - Рис. 1.6. В такой постановке для определения минерального состава кристаллизующихся ассоциаций необходимо иметь систему уравнений, которые однозначно связывают температуру равновесия с расплавом для каждого минерала с составом этого расплава. - заданная точность по температуре. Соотношения (1.16) по существу определяют точку пересечения ликвидусных поверхностей различных фаз - Рис. 1.6. В такой постановке для определения минерального состава кристаллизующихся ассоциаций необходимо иметь систему уравнений, которые однозначно связывают температуру равновесия с расплавом для каждого минерала с составом этого расплава.
Для решения этих задач Натан и Ванкирк предложили использовать эмпирические уравнения вида
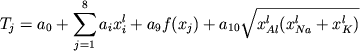 , (1.17) , (1.17)
где  - регрессионные коэффициенты, - регрессионные коэффициенты, 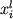 - состав расплава в пересчете на 9 катионов (Si, Al, Ti, Fe3+, Fe2+, Mg, Ca, Na, K), - состав расплава в пересчете на 9 катионов (Si, Al, Ti, Fe3+, Fe2+, Mg, Ca, Na, K), 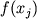 - особая для каждого минерала функция состава силикатной жидкости. В результате статистической обработки значительного объема экспериментальных данных по температурам кристаллизации силикатов уравнения вида (1.17) были получены для 9 главных минералов - оливина, плагиоклаза, авгита, ортопироксена, магнетита, ортоклаза, нефелина, лейцита и кварца (Nathan, Vankirk, 1978). - особая для каждого минерала функция состава силикатной жидкости. В результате статистической обработки значительного объема экспериментальных данных по температурам кристаллизации силикатов уравнения вида (1.17) были получены для 9 главных минералов - оливина, плагиоклаза, авгита, ортопироксена, магнетита, ортоклаза, нефелина, лейцита и кварца (Nathan, Vankirk, 1978).
При наличии быстрого и надежного способа определения минералов на ликвидусе проблема расчета валового состава кристаллизующейся ассоциации сводится к оценке составов этих минералов и пропорций их кристаллизации. Для решения первого вопроса было предложено использовать коэффициенты сокристаллизации типа
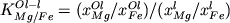 или или 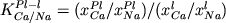 , (1.18) , (1.18)
которые рассчитывались на основании экспериментальных и петрологических данных и не зависели от температуры (Nathan, Vankirk, 1978). Задача расчета пропорций кристаллизации непосредственно связана с алгоритмом моделирования траекторий фракционирования. Последовательность этих операций иллюстрирует схема, приведенная на Рис. 1.7.
В соотвествии с этой схемой, начальное состояние магматической системы всегда отвечает присутствию заданного количества расплава, имеющего известный состав и не содержащего равновесной твердой фазы (степень фракционирования расплава 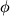 = 0). Условия вида (1.16, 1.17) позволяют оценить температуру ликвидуса и определить минеральные фазы, которые должны кристаллизоваться из расплава. Состав этих фаз рассчитывается по уравнениям типа (1.18). Если температуре ликвидуса отвечает присутствие двух минеральных фаз j1 и j2, то фракционирование осуществляется путем удаления (вычитания) из системы этих минералов в некоторых заданных соотношениях, например 2:1. При этом вычитаемые количества минералов должны удовлетворять условию = 0). Условия вида (1.16, 1.17) позволяют оценить температуру ликвидуса и определить минеральные фазы, которые должны кристаллизоваться из расплава. Состав этих фаз рассчитывается по уравнениям типа (1.18). Если температуре ликвидуса отвечает присутствие двух минеральных фаз j1 и j2, то фракционирование осуществляется путем удаления (вычитания) из системы этих минералов в некоторых заданных соотношениях, например 2:1. При этом вычитаемые количества минералов должны удовлетворять условию 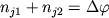 , где , где 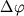 - заданное приращение количества твердой фазы. - заданное приращение количества твердой фазы.
Соотношения (1.15) позволяют рассчитать состав новообразованного расплава 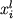 , но может оказаться, что новые (псевдо)ликвидусные температуры , но может оказаться, что новые (псевдо)ликвидусные температуры 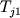 и и 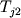 (1.17) уже не отвечают условиям котектической кристаллизации (1.16). Это означает, что для "попадания" на котектическую поверхность необходимо дополнительно кристаллизовать (1.17) уже не отвечают условиям котектической кристаллизации (1.16). Это означает, что для "попадания" на котектическую поверхность необходимо дополнительно кристаллизовать 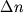 количество твердой фазы, имеющей максимальное значение температуры количество твердой фазы, имеющей максимальное значение температуры 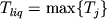 : в результате происходит увеличение значения : в результате происходит увеличение значения 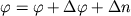 и изменение состава фракционирующего расплава. Процедура дополнительной кристаллизации выполняется попеременно для всех котектических фаз до тех пор, пока их (псевдо)ликвидусные температуры не будут отвечать условиям (1.16). При этом соотношения интегральных количеств кристаллизовавшихся минералов и есть искомые пропорции кристаллизации. Они могут быть использованы на следующем шаге фракционирования в качестве более надежного прогноза, способствующего увеличению быстродействия данной вычислительной схемы (Nathan, Vankirk, 1978). Не трудно заметить, что при реализации данного алгоритма нет необходимости изначально разбивать траекторию фракционирования на фиксированные отрезки кристаллизации различных котектических ассоциаций или задавать пропорции кристаллизации минералов (Drake, 1976a; French, Cameron,1981;Petitpierre, Boivin, 1983). Эти пропорции рассчитываются в ходе моделирования кристаллизации и зависят исключительно от формы уравнения ликвидуса для каждого минерала (Рис.1.6.). и изменение состава фракционирующего расплава. Процедура дополнительной кристаллизации выполняется попеременно для всех котектических фаз до тех пор, пока их (псевдо)ликвидусные температуры не будут отвечать условиям (1.16). При этом соотношения интегральных количеств кристаллизовавшихся минералов и есть искомые пропорции кристаллизации. Они могут быть использованы на следующем шаге фракционирования в качестве более надежного прогноза, способствующего увеличению быстродействия данной вычислительной схемы (Nathan, Vankirk, 1978). Не трудно заметить, что при реализации данного алгоритма нет необходимости изначально разбивать траекторию фракционирования на фиксированные отрезки кристаллизации различных котектических ассоциаций или задавать пропорции кристаллизации минералов (Drake, 1976a; French, Cameron,1981;Petitpierre, Boivin, 1983). Эти пропорции рассчитываются в ходе моделирования кристаллизации и зависят исключительно от формы уравнения ликвидуса для каждого минерала (Рис.1.6.).
Положительной стороной алгоритма Натана и Ванкирка является также то, что он не накладывает ограничений на число компонентов силикатной жидкости и может быть распространен на магматические системы сложного химического состава. Эта несколько модифицированная вычислительная процедура составляет важный элемент ЭВМ-программ, разработанных в последующие годы в нашей группе (Арискин, Френкель, 1982; Френкель, Арискин, 1984), а также серии моделей, представленных Нильсеном с коллегами (Nielsen, Dungan, 1983; Nielsen, 1990).
Назад | Оглавление| Далее
3 Многолетний опыт работы по моделированию фазовых равновесий и обсуждений полученных результатов убедил авторов в том, что далеко не все петрологи проводят четкие различия между пропорциями кристаллизации и пропорциями кристаллических фаз в системе. В первом случае, речь идет о доле j - минерала в конкретной котектической ассоциации, кристаллизующейся на заданном интервале степеней фракционирования ( 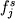 ), а во втором - подразумевается общая доля j - минерала в материале, представляющем интегральный результат кристаллизационного процесса ( ), а во втором - подразумевается общая доля j - минерала в материале, представляющем интегральный результат кристаллизационного процесса (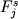 ). ).
А.А. Арискин/ГЕОХИ РАН
 |
Оценка условий кристаллизации ареального вулканизма г. Терпук Срединного хребта, Камчатки.: Content |
|
 |
Оценка условий кристаллизации ареального вулканизма г. Терпук Срединного хребта, Камчатки.: Introduce |
|
 |
Бураковско-Агранозёрский расслоенный массив Заонежья: II. Строение краевой группы и оценка состава родоначальной магмы методом геохимической термометрии: Геохимическая термометрия пород краевой группы |
|
 |
Бураковско-Агранозёрский расслоенный массив Заонежья: II. Строение краевой группы и оценка состава родоначальной магмы методом геохимической термометрии: Список литературы |
|
 |
Эволюция высокоглиноземистых базальтов Ключевского вулкана (Камчатка) по данным изучения магматических включений в минералах: Аналитические методы |
|
 |
Эволюция высокоглиноземистых базальтов Ключевского вулкана (Камчатка) по данным изучения магматических включений в минералах: Методы исследования расплавных включений в минералах |
|
|
|
|
|
|


