Моделирование фазовых равновесий при кристаллизации базальтовых магм
|
Условные обозначения |
Авторы: А.А.Арискин, Г.С.Бармина
Лаборатория термодинамики и математического моделирования природных процессов ГЕОХИ РАН
(Моделирование фазовых равновесий при кристаллизации базальтовых магм.-М.:Наука,МАИК "Наука/Интерпериодика",2000.-363с.) |
Назад | Оглавление| Далее
Используя базу данных ИНФОРЭКС-4.0, мы провели поиск экспериментов по плавлению образцов земных изверженных пород и синтетических базальтовых смесей, где в качестве продуктов закалки присутствует обогащенная железом и титаном шпинель. Задача ставилась следующим образом: из числа экспериментов, проведенных при атмосферном давлении в отсутствии летучих компонентов, найти опыты, где имеются данные по составам расплавов, равновесных с титаномагнетитом 19 .В результате этого поиска было найдено 213 экспериментов из 22 работ, причем примерно половина из них относится к опытам с образцами щелочных базальтов и нефелинитов. Для последующего анализа из этой выборки мы выбрали только опыты в системах низкой и умеренной щелочности, введя дополнительные ограничения на составы закалочных стекол (Na2O+K2O < 7 мас.%) и продолжительность плавок (не менее 48 часов). В базе данных ИНФОРЭКС было найдено 99 экспериментов, отвечающих этим критериям и представляющих 13 независимых исследований.
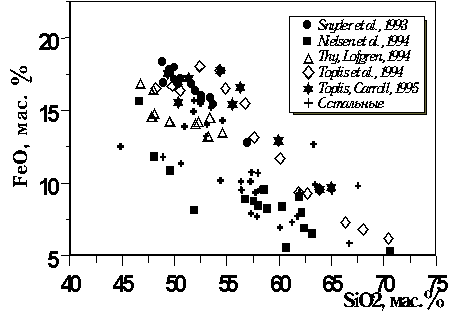
Большинство этих экспериментов характеризуют системы ферро-базальтового и ферроандезит-базальтового состава (10-18 мас.% FeO, Рис. 4.7), при вариациях содержания TiO2 в остаточных расплавах от 1 до 5 мас.%. Диапазон температур кристаллизации титаномагнетита составляет 1040-1160оС (Рис. 4.8).
 |
|
Рис. 4.7. Характеристики состава базовой выборки экспериментальных стекол, отвечающих равновесию магнетит-расплав
|
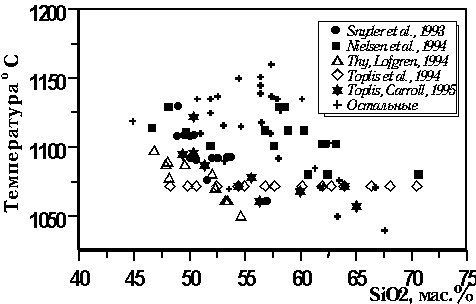 |
| Рис. 4.8. Зависимость температуры ликвидуса от состава для базовой выборки экспериментальных стекол, отвечающих равновесию магнетит-расплав |
Все опыты проведены методом "платиновой петли" в условиях контролируемой фугитивности кислорода, которая менялась в диапазоне 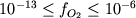 бар: это отвечает интервалу буферных равновесий IW - NNO+2 (Рис. 4.9). Полученные в результате этих экспериментов фазовые ассоциации включают обычно 4-5 минералов + закалочное стекло, причем за исключением нескольких случаев, 4-й или 5-й кристаллизующейся фазой является именно Mt. Плагиоклаз присутствует на ликвидусе всех 99 составов; фемические фазы представлены Ol, Aug, Pig и Opx в различных сочетаниях. В 49 опытах установлено присутствие ильменита: появление этой фазы отмечается для экспериментов в восстановительных условиях log fO2 < -10. бар: это отвечает интервалу буферных равновесий IW - NNO+2 (Рис. 4.9). Полученные в результате этих экспериментов фазовые ассоциации включают обычно 4-5 минералов + закалочное стекло, причем за исключением нескольких случаев, 4-й или 5-й кристаллизующейся фазой является именно Mt. Плагиоклаз присутствует на ликвидусе всех 99 составов; фемические фазы представлены Ol, Aug, Pig и Opx в различных сочетаниях. В 49 опытах установлено присутствие ильменита: появление этой фазы отмечается для экспериментов в восстановительных условиях log fO2 < -10.
 |
| Риc. 4.9. Зависимость летучести кислорода от температуры для базовой выборки экспериментальных стекол, отвечающих равновесию магнетит-расплав |
Обзор специальных исследований стабильности магнетита
Наиболее представительные исследования включают 5 работ (Snyder et al., 1993; Nielsen et al., 1994; Thy, Lofgren, 1994; Toplis et al., 1994b; Toplis, Carroll, 1995), на результатах которых имеет смысл остановиться подробнее.
(1) Snyder et al. (1993). В этой работе приведены результаты 53 опытов на образцах ферробазальтов, которые по составу рассматриваются в качестве аналогов продуктов фракционирования исходных магм для одного из расслоенных комплексов Лабрадора и Скергаардского интрузива (Табл. 4.1). За исключением 3-х случаев, эти опыты проведены в диапазоне температур 1060-1190оС и значений 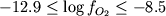 . Для 18 экспериментов среди закалочных продуктов установлен магнетит; в 15 случаях определены составы сосуществующих закалочных стекол (см. залитые кружки на Рис. 4.7-4.9). Важно отметить, что все магнетитсодержащие ассоциации (Ol+Pl+Mt Px Ilm) получены в экспериментах продолжительностью t > 100 часов, что позволяет предполагать близкие к равновесным условия. Полученные данные показывают, что температуры кристаллизации титаномагнетита не превышают 1130оС и при летучести fO2 близкой буферу QFM сильно зависят от окислительно-восстановительных условий (на Рис. 4.9 эта область расположена посередине между линиями WM и NNO). Выделение Mt приводит к резкому обеднению расплавов FeO и обогащению SiO2 (Рис. 4.7). . Для 18 экспериментов среди закалочных продуктов установлен магнетит; в 15 случаях определены составы сосуществующих закалочных стекол (см. залитые кружки на Рис. 4.7-4.9). Важно отметить, что все магнетитсодержащие ассоциации (Ol+Pl+Mt Px Ilm) получены в экспериментах продолжительностью t > 100 часов, что позволяет предполагать близкие к равновесным условия. Полученные данные показывают, что температуры кристаллизации титаномагнетита не превышают 1130оС и при летучести fO2 близкой буферу QFM сильно зависят от окислительно-восстановительных условий (на Рис. 4.9 эта область расположена посередине между линиями WM и NNO). Выделение Mt приводит к резкому обеднению расплавов FeO и обогащению SiO2 (Рис. 4.7).
Таблица 4.1. Составы исходных образцов, использованных при экспериментальных исследованиях равновесия магнетит-расплав
| Ссылка |
Snyder et al., 199
|
Nielsen et al., 1994
|
Thy, Logfren, 1994
|
Toplis et al., 1994-95
|
|
Обр.
|
4-3
|
4-83C
|
SK
|
T85-77
|
121492
|
V-31
|
9005
|
7159V
|
8754
|
SAX2
|
SC4
|
SC1
|
SC4a
|
|
SiO2
|
48.63
|
47.07
|
50.28
|
45.87
|
50.64
|
63.83
|
48.31
|
48.37
|
47.50
|
46.18
|
50.47
|
48.75
|
49.45
|
|
TiO2
|
2.33
|
3.90
|
2.56
|
4.14
|
2.96
|
0.74
|
4.52
|
4.01
|
4.08
|
3.80
|
4.38
|
2.90
|
4.37
|
|
Al2O3
|
14.57
|
13.65
|
13.69
|
15.16
|
15.05
|
15.09
|
13.11
|
13.80
|
12.59
|
15.23
|
11.73
|
14.89
|
11.68
|
|
FeO*
|
14.71
|
17.65
|
13.28
|
12.54
|
14.23
|
8.31
|
14.90
|
14.26
|
15.22
|
13.59
|
14.89
|
13.09
|
16.45
|
|
MnO
|
0.21
|
0.22
|
0.26
|
0.18
|
0.23
|
0.20
|
0.21
|
0.19
|
0.23
|
0.23
|
-
|
-
|
-
|
|
MgO
|
6.29
|
4.75
|
6.58
|
5.16
|
4.57
|
0.36
|
4.82
|
3.31
|
5.17
|
5.47
|
4.89
|
6.49
|
4.67
|
|
CaO
|
9.27
|
7.72
|
10.22
|
11.04
|
8.46
|
4.27
|
9.41
|
9.04
|
10.93
|
10.43
|
10.20
|
10.89
|
9.85
|
|
Na2O
|
3.05
|
3.63
|
2.62
|
3.53
|
2.39
|
4.13
|
3.21
|
4.87
|
3.25
|
3.29
|
2.96
|
2.70
|
3.05
|
|
K2O
|
0.72
|
1.05
|
0.51
|
1.87
|
0.95
|
2.87
|
0.89
|
1.28
|
0.65
|
1.06
|
0.49
|
0.30
|
0.50
|
|
P2O5
|
0.23
|
0.36
|
0.00
|
0.50
|
0.52
|
0.19
|
0.60
|
0.88
|
0.38
|
0.72
|
-
|
-
|
-
|
Примечание. Составы образцов пересчитаны на безводную основу; все железо в виде FeO
(2) Nielsen et al. (1994) привели данные 16 экспериментов на 7 образцах базальтов и андезитов (составы некоторых из них представлены в Табл. 4.1). Эти опыты направлены на изучение стабильности магнетита в условиях несколько выше и ниже буфера NNO; таким образом, Mt присутствует на ликвидусе всех 16 составов. Эксперименты проводились при температурах 1080-1129оС в диапазоне фугитивностей кислорода 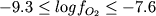 ; длительность опытов составляла не менее 72 часов. Данные Рис. 4.7-4.9 (см. залитые квадраты) подтверждают зависимость температуры кристаллизации Mt от летучести кислорода, при этом обеднение расплавов FeO и обогащение SiO2 отмечается как для базальтовых, так и для андезитовых составов. ; длительность опытов составляла не менее 72 часов. Данные Рис. 4.7-4.9 (см. залитые квадраты) подтверждают зависимость температуры кристаллизации Mt от летучести кислорода, при этом обеднение расплавов FeO и обогащение SiO2 отмечается как для базальтовых, так и для андезитовых составов.
(3) Thy and Lofgren (1994) исследовали влияние состава расплава на температуры кристаллизации магнетита вдоль буфера QFM (треугольники на Рис. 4.9). В качестве исходных составов в этих опытах использовались 4 образца умеренно щелочных ферробазальтов, содержащих 13.5-15.2 мас.% FeO и 3.9-6.1 мас.% Na2O+K2O (Табл. 4.1). Для 15 из 46 проведенных опытов в конечных продуктах было установлено наличие магнетита (  часов). Температуры кристаллизации Mt в этих экспериментах варьируют от 1051оС до 1098оС, при этом тренды обеднения расплавов FeO и обогащения SiO2 проявлены весьма отчетливо (Рис. 4.7). Важный вывод этой работы состоит в том, что независимо от исходного состава, начальные температуры появления Mt в кристаллизационной последовательности составляют 1105 5оС. часов). Температуры кристаллизации Mt в этих экспериментах варьируют от 1051оС до 1098оС, при этом тренды обеднения расплавов FeO и обогащения SiO2 проявлены весьма отчетливо (Рис. 4.7). Важный вывод этой работы состоит в том, что независимо от исходного состава, начальные температуры появления Mt в кристаллизационной последовательности составляют 1105 5оС.
(4) Toplis et al. (1994b) представили результаты 34 изотермических опытов при T=1072oC с образцом синтетического ферробазальта, дозированным различными количествами P2O5 (Табл.4.1, 11-я колонка). Хотя эта работа акцентирована на изучение влияния фосфора на фазовые равновесия силикатных фаз, она включает данные 15 экспериментов, где ликвидусной фазой является Mt (незалитые ромбики на Рис. 4.7-4.9). Продолжительность экспериментов составляла не менее 149 часов, а спектр составов закалочных стекол охватывает диапазон от ферробазальтов до дацитов. По результатам этих опытов магнетит кристаллизуется в интервале буферных равновесий примерно от QFM-0.7 до QFM+1.9.
(5) Toplis and Carroll (1995) дополнили результаты предыдущего исследования 10 новыми экспериментами в области равновесия Mt-расплав. Эксперименты проводились с образцами трех синтетических ферробазальтов (Табл.4.1, колонки 11-13) при температурах 1057-1122оС в диапазоне -11.2 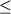 logfO2 logfO2 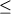 -8.1. Длительность опытов составляла более 115 часов: на Рис. 4.7-4.9 эти данные обозначены шестиконечными звездочками. Как и для рассмотренных выше экспериментов, составы закалочных стекол указывают на закономерное понижение содержания FeO от "базальтов" к "дацитам", при этом в области андезит-дацитовых составов температуры кристаллизации Mt варьируют около 1070оС. Работа (Toplis, Carroll, 1995) представляет по-видимому наиболее полный анализ проблемы фазовых соотношений и расплавно-минеральных равновесий при кристаллизации толеитовых магм с участием магнетита и ильменита. -8.1. Длительность опытов составляла более 115 часов: на Рис. 4.7-4.9 эти данные обозначены шестиконечными звездочками. Как и для рассмотренных выше экспериментов, составы закалочных стекол указывают на закономерное понижение содержания FeO от "базальтов" к "дацитам", при этом в области андезит-дацитовых составов температуры кристаллизации Mt варьируют около 1070оС. Работа (Toplis, Carroll, 1995) представляет по-видимому наиболее полный анализ проблемы фазовых соотношений и расплавно-минеральных равновесий при кристаллизации толеитовых магм с участием магнетита и ильменита.
Отметим три важных результата этого анализа. Во-первых, по данным расчетов с использованием составов и пропорций экспериментальных продуктов установлено, что доля титаномагнетита в ассоциациях, кристаллизующихся в открытых по кислороду условиях, может достигать 15-22 мас.% - очевидно, это главный фактор, определяющий обогащение остаточных расплавов SiO2 при выделении Mt-содержащих парагенезисов. Во-вторых, в интервале буферных равновесий от QFM-2 до QFM+1 наклон ликвидусной температуры Mt в зависимости от fO2 составляет примерно 30оС/lоgfO2. И в-третьих, для насыщенных магнетитом расплавов установлено, что существует отрицательная корреляция между обратной температурой и содержанием в жидкости Fe2O3: это означает, что высоким температурам кристаллизации магнетита отвечает повышенная окисленность железа в расплавах. Последовательного анализа зависимости температуры насыщения Mt от состава расплава и редокс условий Топлис и Кэрролл не представили.
Проблема расчета Fe3+/Fe2+ в расплавах
Логичный способ построения модели для предсказания стабильности магнетита в силикатных расплавах заключается в оценке отношения Fe3+/Fe2+ в жидкости, расчете констант равновесия реакций кристаллизации, калибровке соответствующих температурно-композиционных зависимостей и разработке на этой основе ЭВМ-программы, описывающей поведение твердых растворов магнетита (Nielsen, Dungan, 1983; Ghiorso, 1985; Арискин и др., 1987). Несмотря на то, что эти программы доказали свою применимость при интерпретации трендов фракционирования ферробазальтовых магм (см. выше), их внедрение в практику петрологических исследований вызвало определенные нарекания. В Главе 2 мы уже отмечали, что программа КОМАГМАТ-3.0 (Ariskin et al., 1993) на 20-40оС завышала модельные температуры кристаллизации Mt при летучести кислорода выше QFM, что приводило к занижению оценок fO2 по петрохимическим трендам или неудобствам, связанным с необходимостью периодических температурных коррекций. Не менее неприятная ситуация выявилась при тестировании последней версии программы MELTS (Ghiorso, Sack, 1995): расчеты в условиях переменного режима fO2 указывали на понижение модельной температуры Mt при увеличении 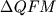 и повышении окисленности расплава (Toplis, Carroll, 1996). и повышении окисленности расплава (Toplis, Carroll, 1996).
По нашему мнению, главная причина этих расхождений кроется в проблемах оценки и использования валового отношения Fe3+/Fe2+ в силикатной жидкости для низкотемпературных Mt-содержащих парагенезисов. Эти проблемы включают три момента:
(1) Данные анализа экспериментальной информации по редокс-равновесиям, имеющейся в базе данных ИНФОРЭКС (всего 372 опыта), показывают, что при калибровке уравнений зависимости Fe3+/Fe2+ в расплаве от состава и температуры около 40% данных представляли сильно окисленные жидкости при fO2 > 10-3 бар, тогда как только 6 экспериментальных стекол были получены при fO2 < 10-9 бар (Fudali, 1965; Shibata, 1967; Sack et al., 1980; Thornber et al., 1980; Kilinc et al., 1983; Kress, Carmichael, 1988, 1991 - см. раздел 2.3). Таким образом, значительная часть исходных данных относится к условиям fO2, далеко выходящим за диапазон, характерный для кристаллизации толеитовых магм (Carmichael, Ghiorso ., 1986, 1990), и слабо перекрывается с пределами стабильности магнетита, установленной по данным специальных исследований - Рис. 4.9. С этим связана дополнительная проблема: сравнение точности уравнений для расчета окисленности железа в магматических расплавах показывает, что для условий logfO2 < -10 относительная погрешность оценок Fe3+/Fe2+ может достигать 50% при абсолютной точности 0.03 (Николаев и др., 1996).
(2) Кинетические эксперименты, проведенные при 1200oC и fO2 = 10-8 бар, показывают, что для уравновешивания отношения Fe3+/Fe2+ в расплаве с газовой фазой требуется от 5 до 24 часов (Fudali, 1965; Thornber et al., 1980). При fO2 = 10-6 бар продолжительность опытов должна быть увеличена до 48 часов (Fudali, 1965). Если сравнить соотношения между длительность-температура для опытов по изучению редокс-равновесий (n=289) и стабильности магнетита (n=99), то можно заметить, что в первом случае использовались единичные плавки > 48 часов, причем ни один из составов, включающих экспериментально определенные значения Fe3+/Fe2+, не попадает в диапазон температур, характерный для кристаллизации магнетита - 1040-1160oC (Рис. 4.8 и 4.10). Эта проблема становится еще более острой, если учесть, что экспериментальное насыщение расплавов магнетитом происходит не только при низкой температуре, но и в условиях высокой закристаллизованности систем (не менее 20-40%), что требует дополнительного увеличения выдержек для достижения равновесия.
|

|
| Рис. 4.10. Соотношения между температурой и длительностью опытов при исследованиях равновесий Fe3+/Fe2+ в жидкости (n=289)и Mt - расплав (n =99) |
(3) Данные мессбауэровской спектроскопии силикатных стекол показывают, что при Fe3+/ 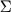 Fe<0.5 окисленное железо (ионы Fe3+) присутствуют в двух разновидностях, включающих тетраэдрическую и октаэдрическую координацию (Mysen et al., 1985). Это означает, что любые попытки рассчитать активность магнетита или Fe2O3 в расплаве на основании валовых отношений Fe3+/Fe2+, будут ошибочны без учета разделения ионов Fe3+ по позициям. Fe<0.5 окисленное железо (ионы Fe3+) присутствуют в двух разновидностях, включающих тетраэдрическую и октаэдрическую координацию (Mysen et al., 1985). Это означает, что любые попытки рассчитать активность магнетита или Fe2O3 в расплаве на основании валовых отношений Fe3+/Fe2+, будут ошибочны без учета разделения ионов Fe3+ по позициям.
Приходится признать, что имеющаяся в настоящее время информация по составу и структурному состоянию силикатной жидкости недостаточна для построения адекватной термодинамической модели равновесия Mt-расплав, даже при условии наличия корректной модели активности компонентов магнетитового твердого раствора (Sack, Ghiorso, 1991; Ghiorso, Sack, 1995). Это приводит к необходимости использовать эмпирические подходы к описанию равновесий с участием Fe-Ti оксидов.
На первом этапе мы поставили задачу построения эмпирического уравнения для расчета температур кристаллизации (ликвидусной поверхности) Ti-Mt в максимально широком диапазоне составов расплавов и летучести кислорода (Арискин, 1998). Описанная выше экспериментальная выборка из 99 составов стекол, закаленных при заданных значениях T и fO2, представляет для этого хорошую эмпирическую основу. Обработка экспериментальных данных проводилась по линейной модели
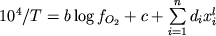 , (4.1) , (4.1)
где T - температура (K), 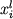 - мольные доли компонентов расплава; b, c и di - регрессионные коэффициенты. При проведении этих вычислений мы умышленно исключили из рассмотрения Fe2O3 как независимого компонента, оперируя только валовыми концентрациями FeOобщ. Это сделано с целью минимизировать погрешности оценок отношения FeO/Fe2O3 в расплавах (см. выше). Другая причина связана с тем, что уравнения, предложенные для расчета FeO/Fe2O3 не учитывают влияния фосфора, которое по последним данным может быть весьма существенным (Toplis et al., 1994ab). Важное отличие этой калибровки состоит также в том, что мы исследовали возможность изменения параметра b при летучести кислорода в зависимости от состава жидкой фазы. - мольные доли компонентов расплава; b, c и di - регрессионные коэффициенты. При проведении этих вычислений мы умышленно исключили из рассмотрения Fe2O3 как независимого компонента, оперируя только валовыми концентрациями FeOобщ. Это сделано с целью минимизировать погрешности оценок отношения FeO/Fe2O3 в расплавах (см. выше). Другая причина связана с тем, что уравнения, предложенные для расчета FeO/Fe2O3 не учитывают влияния фосфора, которое по последним данным может быть весьма существенным (Toplis et al., 1994ab). Важное отличие этой калибровки состоит также в том, что мы исследовали возможность изменения параметра b при летучести кислорода в зависимости от состава жидкой фазы.
В общей сложности проанализировано более 30 вариантов линейной модели (4.1), где варьировались набор и количество компонентов расплава. Критерием поиска оптимального уравнения являлась точность решения обратной задачи, т.е. статистическая оценка степени отклонения расчетных температур от экспериментальных при заданном составе расплава и летучести кислорода. В результате было установлено, что наиболее сильное влияние на устойчивость магнетита оказывают 4 компонента расплава - SiO2, TiO2, FeOобщ и P2O5, а наилучшей точности решения обратной задачи (порядка 10оС) удается достичь при использовании уравнения вида:
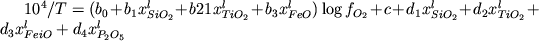 , (4.2) , (4.2)
Таблица 4.2. Регрессионные коэффициенты к уравнению ликвидуса магнетита (4.2)
| Параметр |
коэфф. |
1 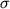 - откл - откл |
| b0 |
-0.6232
|
0.0205
|
| b1 |
0.6826
|
0.0359
|
| b2 |
4.0438
|
0.9327
|
| b3 |
0.8251
|
0.2567
|
| c |
0.0159
|
0.0686
|
| d1 |
8.3626
|
0.2804
|
| d2 |
35.9674
|
8.0819
|
| d3 |
10.7347
|
2.1842
|
| d4 |
12.4418
|
2.3521
|
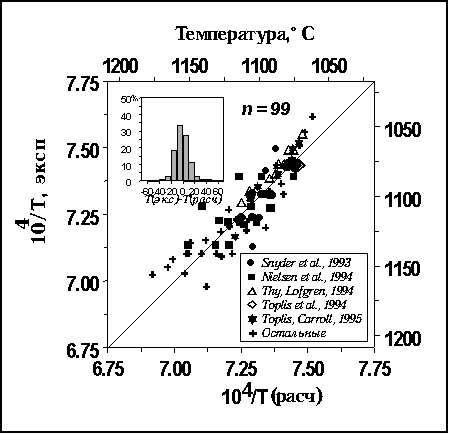
Как видно из этого рисунка, в нескольких случаях эти отклонения достигают 40-50оС, но в целом около 90% данных попадают в интервал 15оС; среднее отклонение 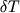 по абсолютной величине составляет 9.3оС. по абсолютной величине составляет 9.3оС.
|
|
|
Рис. 4.11. Экспериментальные и расчетные значения обратной температуры для базовой выборки стекол, отвечающих равновесию магнетит-расплав
Гистограмма дана для отклонений 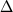 T=Tэксп-Tрасч T=Tэксп-Tрасч
|
Заслуживает внимания, что в случае данных работ (Snyder et al., 1993; Nielsen et al., 1994; Thy, Lofgren, 1994; Toplis et al., 1994b; Toplis, Carroll, 1995) эти отклонения не выходят за пределы 30оС, а для 25 наиболее продолжительных экспериментов (Toplis et al., 1994b; Toplis, Carroll, 1995) среднее значение 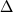 T=3.6оС. Высокая степень воспроизведения представительной выборки экспериментальных данных позволяет предполагать, что найденная форма эмпирической зависимости (4.2) является отражением реальных редокс- и структурно-химических равновесий в жидкой фазе, протекающих с участием ионов Fe3+ и Fe2+ и определяющих условия стабильности на ликвидусе титаномагнетита. T=3.6оС. Высокая степень воспроизведения представительной выборки экспериментальных данных позволяет предполагать, что найденная форма эмпирической зависимости (4.2) является отражением реальных редокс- и структурно-химических равновесий в жидкой фазе, протекающих с участием ионов Fe3+ и Fe2+ и определяющих условия стабильности на ликвидусе титаномагнетита.
Влияние каждого выбранного компонента можно конкретизировать при помощи регрессионных коэффициентов, приведенных в Табл. 4.2. Для этой цели удобно воспользоваться частными производными 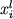 : :
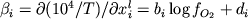 . (4.3) . (4.3)
В случае фосфора 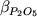 = d4 = 12.4418 > 0 (Табл. 4.2), т.е. увеличение концентрации P2O5 в расплаве приводит к возрастанию обратной температуры или понижению температуры кристаллизации магнетита. Этот эффект не столь уж мал, т.к. добавление 1 мол.% P2O5 может понизить температуру кристаллизации магнетита примерно на 20оС. = d4 = 12.4418 > 0 (Табл. 4.2), т.е. увеличение концентрации P2O5 в расплаве приводит к возрастанию обратной температуры или понижению температуры кристаллизации магнетита. Этот эффект не столь уж мал, т.к. добавление 1 мол.% P2O5 может понизить температуру кристаллизации магнетита примерно на 20оС.
Причины дестабилизирующего влияния фосфора на устойчивость Mt уже анализировались в литературе: прежде всего, это возможность связывания части трехвалентного железа в фосфатные комплексы и понижение общего отношения Fe3+/Fe2+ в расплавах при увеличении концентрации P2O5 (Toplis et al., 1994ab). Дестабилизирующее влияние на магнетит оказывает и возрастание концентраций SiO2 и FeOобщ: из данных Табл. 4.2 и уравнения (4.3) следует, что при logfO2 > -12 обе производные 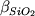 и и 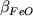 положительны. В отношении SiO2 этот результат выглядит естественно, однако для FeOобщ может вызвать некоторое недоумение. Кажется странным, что стабильность железорудной фазы обратно пропорциональна общему содержанию железа в расплаве. Тем не менее, низкие стандартные отклонения для параметров b3 и d3 (Табл. 4.2) оставляют мало сомнений, что это статистически обоснованное наблюдение. Объяснение данному факту, по-видимому, следует искать в структурно-химических и окислительно-восстановительных реакциях с участием ионов железа. Например, результаты анализа экспериментальных исследований зависимости отношения Fe3+/Fe2+ в силикатных расплавах от состава также показывают, что доля трехвалентного железа понижается с увеличением общей концентрации FeO (Борисов, Шапкин, 1989). положительны. В отношении SiO2 этот результат выглядит естественно, однако для FeOобщ может вызвать некоторое недоумение. Кажется странным, что стабильность железорудной фазы обратно пропорциональна общему содержанию железа в расплаве. Тем не менее, низкие стандартные отклонения для параметров b3 и d3 (Табл. 4.2) оставляют мало сомнений, что это статистически обоснованное наблюдение. Объяснение данному факту, по-видимому, следует искать в структурно-химических и окислительно-восстановительных реакциях с участием ионов железа. Например, результаты анализа экспериментальных исследований зависимости отношения Fe3+/Fe2+ в силикатных расплавах от состава также показывают, что доля трехвалентного железа понижается с увеличением общей концентрации FeO (Борисов, Шапкин, 1989).
Анализ уравнения (4.3) с параметрами для TiO2 указывает на двойственность поведения этого компонента: при logfO2 > -9, добавление титана носит дестабилизирующий характер; в более восстановительных условиях - приводит к возрастанию температуры кристаллизации титаномагнетита, очевидно за счет обогащения твердого раствора Ti-Mt ульвошпинеливым компонентом.
Зависимость температуры кристаллизации Mt от fO2 по разному проявляется в системах различного состава. В соответствии с уравнением ликвидуса (4.2) наиболее сильное влияние окислительно-восстановительных условий можно ожидать для ферробазальтовых составов, характеризующихся низкими и умеренными содержаниями TiO2 и FeO (примерно до 2 и 15 мас.%, соответственно). Для расплавов, обогащенных TiO2 и FeO (типа галапагосских толеитов), данная зависимость может оказаться довольно слабой. Иллюстрацией этого вывода служат результаты, показанные на Рис. 4.12, где приведены температуры ликвидуса титаномагнетита, рассчитанные для 3-х модельных составов (Табл. 4.3) в зависимости от lоgfO2.
|

|
| Рис. 4.12. Зависимости температуры кристаллизации магнетита от летучести кислорода, рассчитанные по уравнению (4.2) для 2-х модельных ферробазальтов и ферроандезита (Табл. 4.3) |
Эти составы представляют условно низко-Ti ферробазальт (BAS-1), ферроандезит (AND) и высоко-Ti ферробазальт (BAS-2). Для каждого из этих составов по программе КОМАГМАТ предварительно были оценены температуры ликвидуса, которые соответствуют для базальтов Ol-Pl котектикам (~ 1165 и ~ 1135о С), а для андезита несколько пересыщенной плагиоклазом системе с температурой ликвидуса около 1125оС.
Таблица 4.3. Модельные расплавы
|
Обр.
|
BAS-1
|
AND
|
BAS-2
|
|
SiO2
|
50.0
|
60.0
|
48.0
|
|
TiO2
|
2.0
|
0.5
|
4.0
|
| Al2O3 |
15.0
|
16.0
|
13.5
|
|
FeO
|
15.0
|
10.0
|
17.5
|
|
MnO
|
-
|
-
|
-
|
|
MgO
|
6.0
|
3.0
|
5.0
|
|
CaO
|
9.0
|
5.5
|
9.0
|
|
Na2O
|
2.5
|
3.5
|
2.5
|
|
K2O
|
0.5
|
1.5
|
0.5
|
|
P2O5
|
-
|
-
|
-
|
|
TPl,oC
|
1164
|
1126
|
1142
|
|
TOl,oC
|
1164
|
1094
|
1133
|
Эта величина примерно в 1.5 раза ниже, чем оценено в работе (Toplis, Carroll, 1995), однако при этом надо учитывать, что в отличии от данных авторов наши оценки получены при условии неизменности состава расплава. Не трудно видеть, что по результатам расчетов понижение lоgfO2 от -6 до -7 при переходе от ферробазальта BAS-1 к ферроандезиту эквивалентно понижению магнетитового ликвидуса примерно на 35оС (Рис. 4.12). Таким образом, предложенное уравнение устойчивости магнетита реалистично воспроизводит закономерности, установленные в опытах с системами переменного состава.
В случае высокотитанистого ферробазальта BAS-2 в широком диапазоне летучести кислорода не наблюдается насыщения системы титаномагнетитом, поскольку расчетные температуры варьируют около 1100оС, что на 25-30оС ниже ликвидусной температуры оливина и плагиоклаза. Очевидно, что при кристаллизации в такого рода системе температура первого появления Mt буферируется составом и не будет сильно отличаться от 1100оС, если не произойдет существенного обогащения расплава SiO2 или обеднения титаном.
Несмотря на то, что эмпирическое уравнение ликвидуса (4.2) полезно для общего анализа влияния состава и fO2 на температуру кристаллизации титаномагнетита (Арискин, 1998), существуют причины, которые не позволяют использовать его при разработке моделей равновесия Mt-расплав: (1) уравнение ликвидуса было построено независимо от состава магнетита, который помимо Fe2O3, FeO и TiO2 обычно включает заметные количества MgO и Al2O3; (2) в результате применения МНК интегральный эффект влияния состава оказался сильнее зависимости от fO2.
Второе обстоятельство особенно существенно: наши попытки интегрировать ур-е (4.2) в КОМАГМАТ оказались неудачными, т.к. приводили к чрезмерно сильному обеднению расплава FeOобщ и обогащению SiO2, чем следовало ожидать исходя из зависимости температуры ликвидуса магнетита от летучести кислорода (Рис. 4.12). Это вызвало необходимость построения более последовательной модели, основанной на калибровке индивидуальных геотермометров Mt-расплав для главных компонентов магнетитовых твердых растворов (Ariskin, Barmina, 1999).
Для решения этой задачи из базовой выборки составов, отвечающих равновесию Mt-расплав (n=99), были выбраны эксперименты, где имеются данные по составам магнетитов - всего 74. В этой выборке были введены дополнительные ограничения на состав Ti-Mt (Cr2O3 < 3 мас.%) и расплава (46 < SiO2 < 70 мас.%, P2O5 < 1.5 мас.%): этим критериям отвечают данные 62 экспериментов. Новая выборка составов была использована для построения 5-ти эмпирических геотермометров, описывающих распределение ионов Fe3+, Fe2+, Ti4+, Al3+ и Mg2+ между магнетитом и силикатной жидкостью в зависимости от состава расплава и летучести кислорода.
Учитывая, что железо и титан входят в состав твердой фазы и при расчете их концентраций в расплаве используется содержание SiO2, мы исключили эти компоненты из числа "независимых", добавив в уравнение регрессии щелочи:
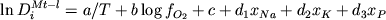 , (4.4) , (4.4)
где 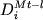 представляет мольные коэффициенты распределения ионов Fe3+, Fe2+, Ti4+, Al3+ и Mg2+ между Fe-Ti шпинелидом и расплавом; xNa, xK и xP - мольные доли Na, K и P в жидкости в пересчете на однокатионный базис; a, b, c, d1, d2 и d3 - регрессионные коэффициенты. Отметим, что при расчетах "коэффициентов распределения" Fe3+ и Fe2+ не используются оценки концентраций этих ионов в жидкости при помощи уравнений Сэка или Килинка, а подставляются валовые содержания железа в расплаве. С позиций термодинамики этот подход непоследователен, но имеет то преимущество, что не вносит дополнительных погрешностей, связанных с неопределенностью оценок Fe3+/Fe2+ и структурного состояния железа в расплаве. Это предполагает, что интегральный эффект редокс-реакций в расплаве учитывается эмпирически как результат зависимости от logfO2, щелочности и содержания фосфора. представляет мольные коэффициенты распределения ионов Fe3+, Fe2+, Ti4+, Al3+ и Mg2+ между Fe-Ti шпинелидом и расплавом; xNa, xK и xP - мольные доли Na, K и P в жидкости в пересчете на однокатионный базис; a, b, c, d1, d2 и d3 - регрессионные коэффициенты. Отметим, что при расчетах "коэффициентов распределения" Fe3+ и Fe2+ не используются оценки концентраций этих ионов в жидкости при помощи уравнений Сэка или Килинка, а подставляются валовые содержания железа в расплаве. С позиций термодинамики этот подход непоследователен, но имеет то преимущество, что не вносит дополнительных погрешностей, связанных с неопределенностью оценок Fe3+/Fe2+ и структурного состояния железа в расплаве. Это предполагает, что интегральный эффект редокс-реакций в расплаве учитывается эмпирически как результат зависимости от logfO2, щелочности и содержания фосфора.
Калибровка геотермометров проводилась в две стадии. На первом этапе обрабатывался полный ряд данных, включающих 62 пары состава магнетита и сосуществующего расплава. Затем полученные регрессионные коэффициенты использовались для решения обратной задачи - расчета температуры равновесия Mt-расплав для той же выборки при условии известных фазовых составов и fO2. Если отклонения модельных температур от экспериментальных более чем в 3 раза превышали среднее отклонение по выборке, то эти составы рассматривались как "неравновесные" и исключались из последующей обработки. Как правило, для каждого компонента находилось 10-12 экспериментальных точек, для которых температурные отклонения составляли 60-150oC. Оставшиеся составы вновь обрабатывались по методике МНК, а скорректированные таким образом коэффициенты табулировались для последующего моделирования (Табл. 4.4). Подобная фильтрация данных может вызвать сомнения в правомерности отбрасывания части экспериментальной информации. Личный опыт автора убеждает, онако, что этот подход весьма эффективен в смысле повышения точности геотермометров и адекватности разрабатываемых моделей фазовых равновесий.
Таблица 4.4. Регрессионные коэффициенты для геотермометров магнетит-расплав, калиброванных по результатам экспериментов в сухих системах при давлении 1 атм
|
Компонент
|
a
|
b
|
c
|
d1
|
d2
|
d3
|
|
Fe3+ (n=50)
|
20964.7
(2075.6)
|
0.6159
(0.0252)
|
-8.8187
(1.4730)
|
-10.1838
(2.8384)
|
32.7525
(2.9031)
|
-14.2506
(4.3306)
|
|
Fe2+ (n=53)
|
17013.8
(1815.3)
|
0.1042
(0.0189)
|
-10.1728
(1.2499)
|
-1.5938
(2.6404)
|
14.1291
(2.4465)
|
-11.7925
(3.5610)
|
|
Al (n=51)
|
-17128.7
(2079.7)
|
0.0105
(0.0202)
|
11.5136
(1.4272)
|
-0.8377
(2.7046)
|
-4.8338
(2.4627)
|
5.8200
(3.6922)
|
|
Mg (n=52)
|
14971.4
(2370.5)
|
0.2021
(0.0255)
|
-8.2121
(1.6317)
|
-10.2151
(3.3928)
|
13.6451
(2.8096)
|
-25.1426
(4.6924)
|
|
Ti (n=43)
|
27422.6
(2325.7)
|
-0.1336
(0.0232)
|
-20.3655
(1.5963)
|
10.5126
(3.2761)
|
22.0278
(3.2829)
|
-10.3297
(4.0910)
|
Используя параметры магнетитовых геотермометров из Табл. 4.4, мы рассчитали температуры равновесия Mt-расплав для урезанных выборок составов по каждому из 5-ти компонентов. Точность воспроизведения экспериментальных температур варьировала при этом от 6.4оС (Ti) до 15.6оС (Mg), составляя в среднем около 10оС (Ariskin, Barmina, 1999). Эти зависимости были использованы для построения общей ЭВМ-модели равновесия Mt-расплав, включающей 5 выбранных компонентов.
Новая магнетитовая модель представляет автономную ЭВМ-программу, позволяющую при известном составе расплава и logfO2 рассчитывать не только ликвидусную температуру, но также состав титаномагнетита. В основе этой программы лежит решение нелинейной системы уравнений, включающей 5 геотермометров вида (4.4) и уравнение стехиометрии магнетита:
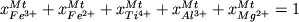 . (4.5) . (4.5)
Для решения этой системы используется алгоритм, построенный по методу последовательных итераций и в главных деталях задействующий принципы построения программы SPINMELT, предназначенной для расчета равновесий хромшпинелид-расплав (Ariskin, Nikolaev, 1996). Тестирование новой магнетитовой модели проведено на составах 32 экспериментальных стекол, полученых в опытах продолжительностью более 100 часов (Grove, Juster, 1989; Snyder et al., 1993; Toplis et al., 1994b; Toplis, Carroll, 1995). Результаты этих расчетов показаны на Рис. 4.13 и демонстрируют хорошую воспроизводимость экспериментальных данных. Это свидетельствует о совместимости и внутренней согласованности индивидуальных геотермометров, использованных для построения обобщенной модели равновесия магнетит-расплав.
 |
|
Рис. 4.13. Сравнение экспериментальных параметров равновесия Mt-расплав с составами и темпера-турами, рассчитанными при помощи новой магнетитовой модели для известных составов расплава и заданной летучести кислорода.
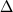 X(ср) и X(ср) и 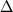 T(ср) представляют средние отклонения расчетных значений от экспериментальных. T(ср) представляют средние отклонения расчетных значений от экспериментальных.
|
Так, модельные составы Mt воспроизводят экспериментальные в среднем с точностью 2.3 мол.% для Fe3+ и Fe2+, 0.5% для Al3+, 0.4% для Mg2+ и 1.3% для Ti4+; при этом погрешности расчета общего содержания железа в Mt (Fe3++Fe2+) составляют около 1 мол.%. Экспериментальные температуры воспроизводятся в пределах 10oC. Новая модель равновесия Mt-расплав интегрирована в программу КОМАГМАТ-3.5 и тестирована на результатах независимого от калибровок экспериментального исследования (Ariskin, Barmina, 1999).
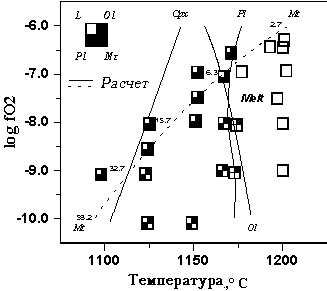
Hill and Roeder (1974) представили данные о стабильности магнетита в зависимости от fO2 для природного ферробазальта Gl-RHB, содержащего ~ 13 мас.% FeO и 2% TiO2 при 51 мас.% SiO2. Эти данные были получены при давлении 1 атм и охватывают широкий диапазон летучести кислорода -14 < logfO2 < -0.68. Мы провели серию редокс-вычислений на этом составе, используя новую версию программы КОМАГМАТ. Как и в случае экспериментов, расчеты проводились при фиксированных значениях logfO2 =-6, -7, -8, -9, и -10 с шагом кристаллизации 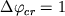 мол.%, от ликвидусной температуры до 1100oC. Это позволило построить диаграмму фазовых соотношений ферробазальта Gl-RHB в зависимости от fO2 и температуры (Рис. 4.14). мол.%, от ликвидусной температуры до 1100oC. Это позволило построить диаграмму фазовых соотношений ферробазальта Gl-RHB в зависимости от fO2 и температуры (Рис. 4.14).
 |
|
Рис. 4.14. Сравнение экспериментальных и расчетных минеральных парагенезисов, образованных при равновесной кристаллизации ферробазальта GL-RHB (Hill, Roeder, 1974)
Расчеты при помощи программы КОМАГМАТ-3.5. Для минимизирования влияния ошибок в расчете температур кристаллизации Ol и Pl на стабильность магнетита, эти температуры скорректированы: TOl увеличена на 15оС, а TPl - на 10оС. Цифры вдоль линии насыщения магнетитом представляют значения Xulv в Mt, рассчитанные по методу (Stormer, 1983).
|
Несмотря на то, что продолжительность опытов (Hill, Roeder, 1974) составляла обычно 48 часов, данные Рис. 4.14 показывают хорошее соответствие результатов расчетов и экспериментов. Магнетит первым кристаллизуется при fO2=10-6 бар и является 4-й фазой в кристаллизационной последовательности при fO2=10-9 бар. Модельные температуры стабильности магнетита отличаются от экспериментальных не более чем на 10-15oC, что соответствует точности разработанной модели равновесия Mt-расплав. Интересно, что рассчитанная зависимость ликвидуса магнетита от fO2 различается в разных окислительно-восстановительных условиях: в диапазоне -7<logfO2<-6 она составляет 30-35oC/logfO2 , а при logfO2 < -10 не превышает 15oC/ logfO2.
Последующий опыт работы с этой моделью показал , что наилучшим образом она "работает" в диапазоне WM < fO2 < NNO. В более окислительных условиях результаты расчетов могут переоценивать температуру ликвидуса магнетита на 15-30oC. Для учета этого фактора в программе КОМАГМАТ-3.5 предусмотрена автоматическая корректировка расчетной температуры для Ti-Mt.
Дальнейшее развитие модели фазовых равновесий связано с учетом кристаллизации ильменита. В основном разделе, посвященном калибровкам уравнений равновесия минерал-расплав, отмечалось, что в версии КОМАГМАТ-3.0 для моделирования выделения ильменита были задействованы уравнения (Nielsen, Dungan, 1983), скорректированные на присутствие Fe2O3 (см. ур-е 2.44). Использование этих соотношений приводило к недооценке ликвидусной температуры Ilm на 20-30оС и его более поздней кристаллизации.
Для разработки новой модели, описывающей равновесия ильменита с расплавами базальтов, была использована такая же последовательность методических приемов, как и для магнетита (Ariskin, Barmina, 1999). В начале был проведен глобальный поиск по базе данных ИНФОРЭКС-4.0, в результате которого было обнаружено 85 пар составов сосуществующих ильменита и закалочных стекол (Juster, Grove, 1989; Snyder et al., 1993; Auwera, Longhi, 1994; Toplis et al., 1994b; Toplis, Carroll, 1995). Из этого ряда данных было исключено 10 экспериментов, где отсутствовали надежные оценки летучести кислорода или Ilm имел нестехиометрический состав (обычно вследствие дефицита ионов Fe3+). Оставшаяся выборка данных 75 экспериментов была использована при последующих калибровках.
Все эти опыты имели продолжительность более 48 часов и проведены в условиях контролируемой фугитивности кислорода 10-13 < fO2 < 10-8 в диапазоне температур 1050-1150oC. Большинство стекол варьируют по составу от ферробазальтов до ферроандезитов при общей щелочности (Na2O+K2O)<7 мас.%. Математическая обработка этих данных проводилась в две стадии на основе линейной регрессии (4.2) для 5-ти катионов - Fe3+, Fe2+, Ti4+, Al3+ и Mg2+. Регрессионные коэффициенты к соответствующим уравнениям равновесия приведены в Табл. 4.5.
Таблица 4.5. Регрессионные коэффициенты для геотермометров ильменит-расплав, калиброванных по результатам экспериментов в сухих системах при давлении 1 атм
|
Компонент
|
a
|
b
|
c
|
d1
|
d2
|
d3
|
|
Fe3+ (n=65)
|
18933.4
(5796.2)
|
0.8475
(0.0469)
|
-8.6100
4.3982)
|
35.4214
(9.8997)
|
28.9571
(9.6089)
|
-8.6859
(7.4175)
|
|
Fe2+ (n=56)
|
2649.1
(903.4)
|
0.0544
(0.0084)
|
-0.4271
(0.6935)
|
-1.8146
(1.7981)
|
20.6115
(2.4139)
|
-1.7339
(1.3306)
|
|
Al (n=66)
|
-14947.7
(2436.5)
|
0.1778
(0.0204)
|
9.4357
(1.8763)
|
0.1175
(4.4802)
|
3.4801
(4.6040)
|
2.6951
(3.4255)
|
|
Mg (n=53)
|
904.8
(1044.4)
|
0.0340
(0.0087)
|
0.1111
(0.7864)
|
-1.6455
(1.7008)
|
14.3103
(1.6868)
|
-6.8648
(1.3100)
|
|
Ti (n=72)
|
12245.2
(974.7)
|
0.0178
(0.0080)
|
-6.6774
(0.7474)
|
5.8720
(1.8045)
|
25.2774
(1.7771)
|
-5.3331
(1.4075)
|
Примечание. В скобках указаны стандартные отклонения (1 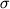 ). ).
Добавление в эту систему геотермометров уравнения стехиометрии для Ilm :
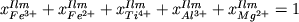 . (4.6) . (4.6)
легко решается относительно температуры и состава твердой фазы при известном составе расплава и летучести кислорода.
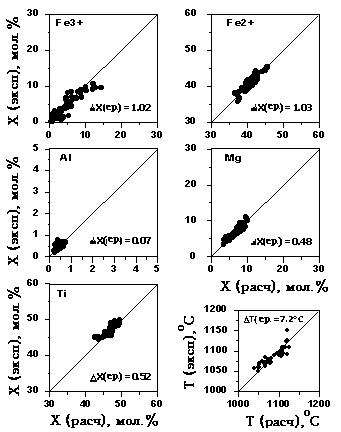
Для оценки точности новой "ильменитовой модели" из базовой выборки составов были выбраны данные 64 экспериментов продолжительностью более 100 часов, которые охватывают диапазон -12.6 < logfO2 < -9. Результаты решения обратной задачи на этой выборке показаны на Рис. 4.15. Эти результаты демонстрируют высокую точность расчета температур кристаллизации ильменита, которая в среднем составляет 7.2oC. Модельные составы Ilm отклоняются от экспериментальных с погрешностями порядка 1 мол.% для Fe3+ и Fe2+; для остальных компонентов средние отклонения составов не превышают полпроцента: 0.07% (Al3+), 0.48% (Mg2+) и 0.52% (Ti4+).
 |
|
Рис. 4.15. Сравнение экспериментальных параметров равновесия Ilm-расплав с составами и темпера-турами, рассчитанными при помощи новой ильменитовой модели для известных составов расплава и заданной летучести кислорода.
D 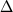 X(ср) и X(ср) и 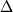 T(ср) представляют средние отклонения расчетных значений от экспериментальных. T(ср) представляют средние отклонения расчетных значений от экспериментальных.
|
Разработанная модель кристаллизации ильменита была также интегрирована в программу КОМАГМАТ-3.5, которая теперь позволяет моделировать сложные эффекты выделения Fe-Ti оксидов в петрологически важном диапазоне летучести кислорода, отвечающей интервалу буферных равновесий примерно от IW до NNO. Отметим, что в новой версии программы КОМАГМАТ составы магнетита и ильменита выводятся в форме катионных долей (Fe3+, Fe2+, Al3+, Mg2+, Ti4+), а также в виде параметров XUlv и XIlm, которые рассчитываются по уравнениям Stormer (1983).
На Рис. 4.16
 |
|
Рис. 4.16. Фазовые диаграммы для ферробазальта SC1 (Табл. 4.1)
А Результаты экспериментов по данным (Toplis, Carroll, 1995, 1996). Б Расчеты, проведенные при помощи программы КОМАГМАТ-3.5. Для минимизирования влияния ошибок в расчете температур кристаллизации Ol и Pl на стабильность Fe-Ti оксидов, эти температуры скорректированы: TOl увеличена на 5оС, а TPl понижена на 15оС.
|
сопоставляются фазовые диаграммы для синтетического ферробазальта SC1 (Табл. 4.1), построенные по результатам экспериментов (Toplis, Carroll, 1995, 1996) и данным расчетов с использованием программы КОМАГМАТ-3.5. Фазовая диаграмма на Рис. 4.16Б сконструирована исходя из 17 траекторий равновесной кристаллизации, рассчитанных в условиях fO2 параллельных буферу QFM для диапазона 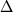 QFM от -2.5 до +1.5 с шагом 0.25 лог. ед. Она интересна тем, что реалистично воспроизводит изменение соотношений между ильменитом и магнетитом вблизи буфера QFM. (преобладание Mt в более окислительных условиях и относительно раннее выделение Ilm в восстановительных). При этом ошибки определения полей устойчивости магнетита и ильменита составляют порядка 10-12oC. QFM от -2.5 до +1.5 с шагом 0.25 лог. ед. Она интересна тем, что реалистично воспроизводит изменение соотношений между ильменитом и магнетитом вблизи буфера QFM. (преобладание Mt в более окислительных условиях и относительно раннее выделение Ilm в восстановительных). При этом ошибки определения полей устойчивости магнетита и ильменита составляют порядка 10-12oC.
Результаты этих расчетов дают важную информацию по пропорциям кристаллизации оксидов: в точке появления Mt на ликвидусе она составляет 35-40 мас.%, что согласуется с данными (Hill, Roeder, 1974; Toplis, Carroll, 1996), однако для основного интервала кристаллизации ассоциации Ol+Pl Aug+Mt, варьирует в пределах 16-22%. Модельная пропорция ильменита более постоянна и колеблется от 8 до 14 мас.%.
Примечание:
19 При наличии состава шпинели отбирались фазы с суммарным содержанием оксидов железа и титана не менее 85% и концентрацией Cr2O3 не более 5%. При отсутствии таких данных отнесение шпинели к титаномагнетиту проводилось на основании описаний авторов.
Назад | Оглавление| Далее
А.А. Арискин/ГЕОХИ РАН
 |
Оценка условий кристаллизации ареального вулканизма г. Терпук Срединного хребта, Камчатки.: Content |
|
 |
Оценка условий кристаллизации ареального вулканизма г. Терпук Срединного хребта, Камчатки.: Introduce |
|
 |
Бураковско-Агранозёрский расслоенный массив Заонежья: II. Строение краевой группы и оценка состава родоначальной магмы методом геохимической термометрии: Геохимическая термометрия пород краевой группы |
|
 |
Бураковско-Агранозёрский расслоенный массив Заонежья: II. Строение краевой группы и оценка состава родоначальной магмы методом геохимической термометрии: Список литературы |
|
 |
Эволюция высокоглиноземистых базальтов Ключевского вулкана (Камчатка) по данным изучения магматических включений в минералах: Аналитические методы |
|
 |
Эволюция высокоглиноземистых базальтов Ключевского вулкана (Камчатка) по данным изучения магматических включений в минералах: Методы исследования расплавных включений в минералах |
|
|
|
|
|
|


