Моделирование фазовых равновесий при кристаллизации базальтовых магм
|
Условные обозначения |
Авторы: А.А.Арискин, Г.С.Бармина
Лаборатория термодинамики и математического моделирования природных процессов ГЕОХИ РАН
(Моделирование фазовых равновесий при кристаллизации базальтовых магм.-М.:Наука,МАИК "Наука/Интерпериодика",2000.-363с.) |
Назад | Оглавление| Далее
Решение задачи моделирования равновесной кристаллизации базальтовых расплавов и включение в этот алгоритм режимов идеального, частичного и промежуточного фракционирования (Рис. 2.28) позволяет использовать программу КОМАГМАТ для решения генетических задач, связанных с оценкой условий формирования вулканических серий и интрузивных базитов. Результаты практического применения моделей фракционной кристаллизации будут даны в Главах 4, 5 и 6. В данной главе мы рассмотрим несколько примеров использования процедуры равновесной кристаллизации, которое получило название метода геохимической термометрии (Арискин, 1985; Френкель и др., 1987).
Информативность оценок состава магматического расплава. Один из важнейших вопросов генетической интерпретации базитов касается определения состава магматического расплава, который можно рассматривать в качестве исходного (родоначального) для выделенной ассоциации изверженных пород. Немаловажное значение имеет и поиск составов производных жидкостей, составляющих серию продуктов фракционирования одной исходной магмы. Составы этих расплавов связаны соотношениями термодинамического равновесия с составами минералов, определяющих направленность фракционирования в магматической системе. Это позволяет использовать методы геотермобарометрии фазовых равновесий для оценки P-T параметров конкретных минеральных парагенезисов, напр. (Перчук, Рябчиков, 1976). С другой стороны, сам набор ликвидусных фаз нередко накладывает жесткие ограничения на температуру, давление и другие параметры равновесия с расплавом заданного состава. Это свойство природных силикатных систем используется для построения различного рода барометрических графиков, типа показанной на Рис. 2.14 псевдотройной диаграммы OLIV-PLAG-QTZ. К сожалению, прямые данные по составам расплавов, составляющих жидкую часть эффузивного материала или захороненных в интеркумулусе интрузивных пород, редки, так что область применимости этих подходов обычно ограничивалась рассмотрением ассоциаций, где возможен отбор стекловатых и афировых разностей пород.
Новые возможности в этом направлении связаны с развитием методов изучения расплавных включений, которые дают оценки состава и температуры силикатной жидкости равновесной с минералом-хозяином в момент захвата включения, напр. (Соболев, 1996). Исследования мантийного магматизма различных геодинамических обстановок с использованием метода термометрии расплавных включений и моделирования обратного хода кристаллизации позволили разделить магматические расплавы на интегральные и дифференциальные, различающиеся по степени проявления процессов смешения расплава в магмогенерирующей системе и подводящих каналах (Соболев, 1997).
Интегральными были названы расплавы, которые в качестве транспортирующей среды выносят к поверхности часть кристаллических продуктов фракционирования и при затвердевании дают реальные магматические породы. К дифференциальным относятся все те неоднородности состава расплавных включений, которые могут быть обнаружены в пределах отдельного кристалла или образца породы при использовании прецезионных методов химического анализа. Предполагается, что дифференциальные расплавы представляют "истинное" разнообразие составов жидкостей, а установленный таким образом разброс их составов объясняется "кристаллизацией вкрапленников в разных частях магматической системы (серия магматических камер и подводящих каналов)..." (Соболев, 1997). Согласно этой гипотезе, интегральные магматические расплавы являются продуктами смешения дифференциальных расплавов.
Предложенная интерпретация петрохимических данных может оказаться полезной для генетических реконструкций. Вместе с тем нельзя не отметить, что информация по включениям дает химические характеристики объектов по существу микроскопических и потому имеющих мало шансов сохраниться в течение периода остывания магматических масс. В середине 80-х годов мы предложили методику геохимической термометрии магматических пород, направленную на оценку параметров исходного предположительно равновесного состояния, информация о котором "записана" в валовых составах эффузивных и интрузивных базитов (Арискин, 1985). Этот подход включает полную фазовую и химическую интерпретацию породы, в том числе расчет температуры и состава транспортирующих или интеркумулятивных расплавов.
Процесс формирования магматической породы можно разделить на несколько стадий, начальное состояние которых включает механическую смесь кристаллов разного вида j и расплава l:
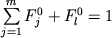 , (3.1) , (3.1)
где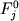 и и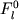 исходные пропорции минеральных зерен и силикатной жидкости. Очевидный пример такой системы дают разнообразные кумуляты, в которых за счет образования зернового каркаса кумулуса (интрузивные базиты) или благодаря быстрому охлаждению (кумулятивные базальты) прекращается относительное перемещение твердых фаз и расплава. Это начальное состояние будем называть моментом формирования породы в геохимическом смысле, подразумевая, что именно на данном этапе формируется ее валовый химический состав, который при условии закрытости системы не меняется в процессах дальнейшего остывания и перекристаллизации. исходные пропорции минеральных зерен и силикатной жидкости. Очевидный пример такой системы дают разнообразные кумуляты, в которых за счет образования зернового каркаса кумулуса (интрузивные базиты) или благодаря быстрому охлаждению (кумулятивные базальты) прекращается относительное перемещение твердых фаз и расплава. Это начальное состояние будем называть моментом формирования породы в геохимическом смысле, подразумевая, что именно на данном этапе формируется ее валовый химический состав, который при условии закрытости системы не меняется в процессах дальнейшего остывания и перекристаллизации.
Валовый состав такой системы может быть рассчитан исходя из относительных пропорций твердых фаз и расплава, состава жидкой фазы %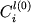 и средневзвешенного содержания главного или примесного элемента во вкрапленниках или кумулятивных зернах данного минерального вида и средневзвешенного содержания главного или примесного элемента во вкрапленниках или кумулятивных зернах данного минерального вида 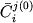 : :
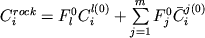 . (3.2) . (3.2)
Параметры этого уравнения дают полное описание начального состояния магматической смеси, при затвердевании которой сформировалась та или иная порода. Это позволяет определить значения 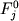 и и 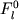 как первичные фазовые пропорции в исходной расплавно-минеральной системе, а как первичные фазовые пропорции в исходной расплавно-минеральной системе, а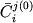 и и 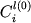 - исходные составы минералов и расплава. Исходный расплав имеет конкретную температуру ликвидуса, которую естественно определить как температуру формирования породы. Данное определение относится только к начальным условиям существования расплавно-минеральной ассоциации: для эффузивных пород это температура транспортирующей магмы, для интрузивных - температура захваченного в интеркумулусе расплава. - исходные составы минералов и расплава. Исходный расплав имеет конкретную температуру ликвидуса, которую естественно определить как температуру формирования породы. Данное определение относится только к начальным условиям существования расплавно-минеральной ассоциации: для эффузивных пород это температура транспортирующей магмы, для интрузивных - температура захваченного в интеркумулусе расплава.
Рассмотренные характеристики процесса формирования породы следует отличать от тех пропорций и минеральных составов, которые доступны прямым наблюдениям петрологов, поскольку в результате последующего остывания смеси и докристаллизации межзерновой жидкости меняется не только состав расплава, но также составы минералов и, вероятно, морфология аггрегатов, отвечающих за структуру формирующейся породы. Это замечание относится также к оценкам температур, рассчитанных в приближении "замороженных минеральных равновесий", которые характеризуют не начальные, а более поздние низкотемпературные стадии затвердевания системы.
Таким образом, "память" об исходном состоянии "записана" именно в валовом химическом составе магматической породы и задача реконструкции условий ее образования заключается в использовании этой информации для оценки первичных фазовых пропорций и составов.
Расчеты по методу баланса масс. Для оценки состава магматической жидкости уравнение (3.2) может быть преобразовано к виду:
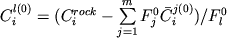 , (3.3) , (3.3)
что подразумевает наличие независимой информации о первичных пропорциях и составах минералов. Данные по составам минералов могут получены в результате микрозондовых исследований, но даже если предположить, что они представляют не смещенные, а исходные характеристики, остается открытым вопрос о первичных фазовых пропорциях. В принципе, они могут быть рассчитаны по данным модального анализа, однако этот подход всегда подразумевает некоторую субъктивную структурную интерпретацию породы. Если для эффузивных пород в качестве первичной ассоциации можно предположить парагенезис фенокристаллов, то для субвулканических и интрузивных пород этот выбор сделать гораздо труднее. Частично разрешить эту ситуацию позволяют методы линейного программирования, основанные на использовании соотношений (3.2) для сильно переопределенного набора главных или примесных элементов (Wright, Doherty, 1970). Но при этом по-прежнему сохраняются неопределенности оценок исходных минеральных составов по микрозондовым данным: наиболее проблематичны они для минералов интрузивных пород, которые в процессе остывания испытывают существенное переуравновешивание (см. ниже).
Существует, однако, одно полезное допущение, которое позволяет отказаться от использования микрозондовых данных и включает учет гипотетической взаимосвязи первичных составов минералов и расплава:
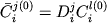 , (3.4) , (3.4)
где 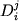 - коэффициент распределения i-го элемента между минералом j и силикатной жидкостью (2.52). Используя экспериментально определенные значения - коэффициент распределения i-го элемента между минералом j и силикатной жидкостью (2.52). Используя экспериментально определенные значения 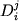 , соотношения (3.4) можно подставить в уравнения (3.2) для различных элементов и решать эти системы относительно состава расплава и первичных фазовых пропорций. Основанные на этом подходе методики получили широкое распространение в последние годы, в частности в связи с интерпретацией спектров распределения редкоземельных элементов в кумулятах, представляющих различные типы базальтоидных ахондритов, напр. (Treiman, Sutton, 1992; Wadhwa et al., 1994). , соотношения (3.4) можно подставить в уравнения (3.2) для различных элементов и решать эти системы относительно состава расплава и первичных фазовых пропорций. Основанные на этом подходе методики получили широкое распространение в последние годы, в частности в связи с интерпретацией спектров распределения редкоземельных элементов в кумулятах, представляющих различные типы базальтоидных ахондритов, напр. (Treiman, Sutton, 1992; Wadhwa et al., 1994).
Несмотря на привлекательность и простоту этого подхода (вопрос о правомерности равновесного приближения пока отложим), он имеет два недостатка. Во-первых, уравнения баланса масс не учитывают зависимости 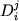 от состава и температуры. С этим связана и другая проблема - задачу поиска первичных фазовых пропорций не удается решить с использованием всего комплекса данных о содержаниях главных и примесных элементов. Представленный ниже метод геохимической термометрии включает комплексное решение этих вопросов. от состава и температуры. С этим связана и другая проблема - задачу поиска первичных фазовых пропорций не удается решить с использованием всего комплекса данных о содержаниях главных и примесных элементов. Представленный ниже метод геохимической термометрии включает комплексное решение этих вопросов.
Основное исходное для предлагаемого метода предположение состоит в том, что в некоторый начальный момент химические составы минералов и расплава были связаны соотношениями термодинамического равновесия (1.26), где в качестве одного из параметров входит температура формирования породы (Арискин, 1985). Эта температура отвечает условиям существования расплавно-минеральной ассоциации и в качестве фактора термодинамического равновесия влияет на распределение между фазами главных компонентов и примесных элементов.
Второе принципиальное предположение заключается в том, что среди множества пород исследуемого магматического объекта имеются образцы, вариации химического состава которых обусловлены только изменением первичных фазовых пропорций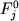 и и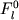 (Френкель и др., 1987). Такие образцы составляют группы пород, образовавшихся при одной и той же температуре из расплава и минералов одного и того же состава. Физических причин, вызывающих подобную неоднородность существует множество - это случайный характер заполнения пространства породы кумулятивным каркасом, неоднородности распределения взвешенных в магме кристаллических фаз, посткумуляционная сортировка минеральных зерен, потоковая дифференциация и многие другие процессы. (Френкель и др., 1987). Такие образцы составляют группы пород, образовавшихся при одной и той же температуре из расплава и минералов одного и того же состава. Физических причин, вызывающих подобную неоднородность существует множество - это случайный характер заполнения пространства породы кумулятивным каркасом, неоднородности распределения взвешенных в магме кристаллических фаз, посткумуляционная сортировка минеральных зерен, потоковая дифференциация и многие другие процессы.
Постоянство состава транспортирующей или захваченной магматической жидкости предполагает два главных варианта генетической и геологической интерпретации таких пород. Во-первых, это может быть следствием локальной неоднородности объекта в масштабе сантиметров и метров (возможно десятков метров для крупных тел), как предельный случай - проявления ритмической расслоенности. Во-вторых - результат отсутствия или слабо проявленного фракционирования магмы, что позволяет предполагать существование одинаковых условий формирования пород в масштабах геологического тела. Как будет ясно из последующего анализа, на основе методов численного моделирования фазовых равновесий можно не только идентифицировать эти группы генетически родственных пород, но также дать их полную фазовую интерпретацию, включая состав расплава и температуру в момент образования.
Практическая реализация. Следуя этим предположениям, можно утверждать, что при моделировании равновесной кристаллизации расплавов пород различного химического состава, но образованных из фаз одной и той же "равновесной" ассоциации, рассчитанные линии эволюции составов расплавов должны давать пересечения в пространстве состав - температура. При этом температуру в точке пересечения следует интерпретировать как общую для всех пород температуру образования, а найденный таким образом состав расплава рассматривать в качестве исходного расплава. Соответственно, рассчитанные в точке пересечения составы минералов будут представлять также исходные содержания миналов и микроэлементов, а модельные пропорции фаз - характерные для каждой породы первичные фазовые пропорции.
Предложенный метод геохимической термометрии заключается в численном моделировании траекторий равновесной кристаллизации для расплавов пород исследуемого магматического объекта и поиске эволюционных линий, образующих в пространстве состав - температура узлы их пересечений.
В случае небольшого количества рассчитанных траекторий кристаллизации (образцов пород) идентификацию области перечения можно проводить путем визуального анализа серии T-X диаграмм для главных и примесных элементов. Большинство последующих примеров применимости метода геохимической термометрии будут основаны на этой методике. Для значительных по объему выборок составов пород необходимо привлекать специальные алгоритмы поиска наиболее компактных и многочисленных сгущений составов, представляющих серии изотермических сечений в (5-10)-мерном пространстве содержаний компонентов. Подходы к решению этой задачи будут рассмотрены в разделе, посвященном геохимической термометрии магматических пород Моря Кризисов на Луне. Однако прежде, чем перейти к петрологическим примерам, обсудим некоторые термодинамические аспекты предложенной методики.
Для информативности результатов поиска пересечений эволюционных линий немаловажен вопрос о размерности траекторий кристаллизации. Процедура физико-химического моделирования представляет их в виде эволюционных линий в (K+1) - мерном пространстве состава и температуры, где K - число компонентов расплава. В действительности необходимо учитывать, что петрогенетическое значение будут иметь линии, располагающиеся в пространстве меньшей размерности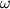 , а именно в пространстве, размерность которого равна вариантности соответствующего многофазового равновесия (Френкель и др., 1987). В простых системах величина , а именно в пространстве, размерность которого равна вариантности соответствующего многофазового равновесия (Френкель и др., 1987). В простых системах величина 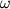 определяется правилом фаз Гиббса, в соответствии с которым при постоянном давлении определяется правилом фаз Гиббса, в соответствии с которым при постоянном давлении
, (3.5)
где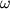 - число степеней свободы, - число степеней свободы,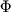 - число фаз в равновесной ассоциации, а - число фаз в равновесной ассоциации, а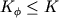 - число фазообразующих компонентов. - число фазообразующих компонентов.
Значение этого фактора становится ясно из анализа траекторий кристаллизации-плавления в простой трехкомпонентной системе с эвтектикой типа Fo-An-Di. Рис. 3.1 показывает, что в эвтектическую точку E (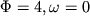 ) сходятся траектории кристаллизации любых составов, линии эволюции которых в координатах состав - температура будут всегда образовывать веер с точкой пересечения, отвечающей параметрам эвтектической смеси. Подобное "пересечение" эволюционных линий в нонвариантной точке не несет дополнительной информации об исходных составах. Менее вероятно случайное попадание траекторий кристаллизации на котектики A+B+l, A+C+l, или B+C+l ( ) сходятся траектории кристаллизации любых составов, линии эволюции которых в координатах состав - температура будут всегда образовывать веер с точкой пересечения, отвечающей параметрам эвтектической смеси. Подобное "пересечение" эволюционных линий в нонвариантной точке не несет дополнительной информации об исходных составах. Менее вероятно случайное попадание траекторий кристаллизации на котектики A+B+l, A+C+l, или B+C+l (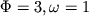 ), однако и в этом случае "пересечение" не является информативным, поскольку обусловлено термодинамическим фактором - одномерностью пространства котектических линий. Принципиально меняет ситуацию добавление в эту систему четвертого компонента D. Даже если этот компонент не является фазообразующим, котектические линии превращаются в поверхности, а точка четырехфазового "эвтектического" равновесия в линию, связывающую температуру и содержание в расплаве компонента D. ), однако и в этом случае "пересечение" не является информативным, поскольку обусловлено термодинамическим фактором - одномерностью пространства котектических линий. Принципиально меняет ситуацию добавление в эту систему четвертого компонента D. Даже если этот компонент не является фазообразующим, котектические линии превращаются в поверхности, а точка четырехфазового "эвтектического" равновесия в линию, связывающую температуру и содержание в расплаве компонента D.
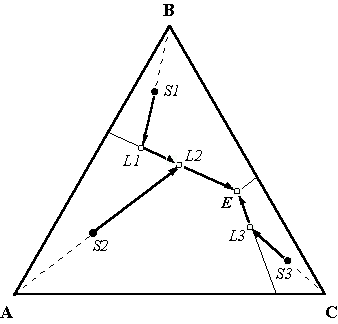 |
Рис. 3.1. Примеры пересечений траекторий кристаллизации в эвтектоидной системе A-B-C с фазами постоянного состава (аналог системы Fo-An-Di)
S1,S2 и S3 - исходные составы; L1,L2 и L3 - составы расплавов этих смесей в момент попадания на котектические линии
|
Это означает, что случайное пересечение линий на какой-либо котектической поверхности (напр., A+B+l) становится маловероятным и возможно при условии, если два или более исходных состава представляют смеси произвольного количества кристаллов A, B и расплава постоянного состава (xA , xB , xC , xD). Таким образом, мы приходим к выводу, что генетический смысл сходимости линий равновесной кристаллизации проявляется в условиях как минимум бивариантного равновесия, когда число компонентов жидкости превышает число фаз расплавно-минеральной ассоциации в точке пересечения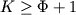 . .
Простейший случай бивариантного равновесия в системах с твердыми растворами приведен на Рис. 3.2 и дает наглядный пример пересечения эволюционных линий, имеющих генетический смысл. Эта диаграмма иллюстрирует следующее утвеждение: в точке бивариантного ликвидусного равновесия L пересекаются траектории равновесной (закрытой) кристаллизации только тех расплавов, составы которых могут быть получены комбинированием в произвольных пропорциях расплава L и равновесного с ним минерала состава S. Доказывается это утверждение от обратного - если бы точку L могли пересекать любые траектории, то это означало бы присутствие в смеси минерала неравновесного с расплавом L. Это утверждение может быть распространено на многокомпонентные системы, включающие несколько минералов - твердых растворов (Френкель и др., 1987).
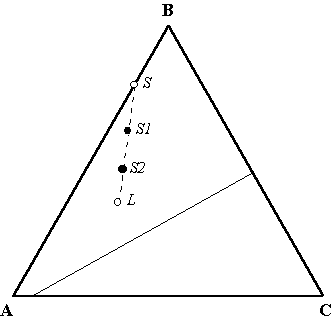 |
Рис. 3.2. Пример пересечений траекторий кристаллизации в эвтектоидной системе A-B-C с фазами переменного (A-B) и постоянного (C) состава (аналог системы Ab-An-Di)
S - состав фазы переменного состава, S1 и S2 - исходные составы на конноде S-L, L - составы расплава, общего для составов S1 и S2
|
Из проведенного анализа следует вывод, что случайное попадание более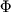 составов в пространство одной коннодной ассоциации невозможно: это и делает наличие пересечений при условии составов в пространство одной коннодной ассоциации невозможно: это и делает наличие пересечений при условии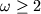 (или (или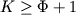 ) генетически информативным. Выполнение данных условий обязательно при проведении геохимической термометрии магматических пород. Учитывая, что общее число фаз в ликвидусных ассоциацииях обычно варьирует от 2 (Ol+l, Pl+l) до 7 (Ol+Pl+Aug+Pig+Mt+Ilm+l), результаты расчетов должны включать анализ содержаний в расплаве от 3-х до 8-ми компонентов, при этом необходимо рассмотреть от 2 до 7 эвоюционных линий. Отметим также, что в системах с твердыми растворами пересечения траекторий кристаллизации проявляются в виде характерной двухвеерной структуры - пучков, визуальная идентификация которых обычно не составляет труда (Арискин, 1985). ) генетически информативным. Выполнение данных условий обязательно при проведении геохимической термометрии магматических пород. Учитывая, что общее число фаз в ликвидусных ассоциацииях обычно варьирует от 2 (Ol+l, Pl+l) до 7 (Ol+Pl+Aug+Pig+Mt+Ilm+l), результаты расчетов должны включать анализ содержаний в расплаве от 3-х до 8-ми компонентов, при этом необходимо рассмотреть от 2 до 7 эвоюционных линий. Отметим также, что в системах с твердыми растворами пересечения траекторий кристаллизации проявляются в виде характерной двухвеерной структуры - пучков, визуальная идентификация которых обычно не составляет труда (Арискин, 1985).
Погрешности вычислений. Здесь следует оговориться, что данные термодинамические выводы верны в идеальном приближении. При практических расчетах из-за погрешностей химического анализа и неопределенностей, связанных с использованием модели фазовых равновесий, точка пересечения траекторий в отношении состава расплава и температуры будет определена с некоторой неточностью, представляя на T-X диаграммах области сгущения линий, см. напр. Рис. 3.4. При работе с программой КОМАГМАТ в толеитовых системах погрешность оценки температуры должна быть порядка точности используемых геотермометров - 10-15оС (Глава 2), а точность определения содержаний главных компонентов - порядка 0.5-1 мас.% (Рис. 2.34 и 2.35).
Главный вопрос о применимости метода геохимической термометрии касается допущения о равновесном характере первичных фазовых ассоциаций. По этой причине наиболее удачным объектом для его использования являются интрузивные базиты, долериты дифференцированных силлов и другие полнокристаллические породы, которые формировались в результате достаточно длительного остывания магматических масс. Косвенным подтверждением субравновесного характера исходных магм в этих объектах являются незначительные вариации состава вкрапленников в породах эндоконтактов, напр. (Hoover, 1989ab).
Более проблематична возможность применения этого метода для термометрии вулканических пород. Данные микрозондовых исследований минералов в базальтах нередко указывают на существенный разброс составов вкрапленников, часть которых обычно интерпретируются как ксенокристаллы. Это указывает на неравновесность первичной ликвидусной ассоциации. В данном случае в качестве критерия правомерности равновесных вычислений и точности оценки состава расплава могут служить отличия между рассчитанным равновесным составом минерала и его средневзвешенным составом в ассоциации фено- и ксенокристаллов: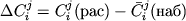 . В общем, на метод геохимической термометрии вулканических пород распространяются все те ограничения, которые должны оговариваться при использовании традиционных методов петрологических интерпретаций, таких как термометрия "равновесий" вкрапленник - основная масса или оценки давлений путем проектирования валовых составов базальтов на физико-химические диаграммы, построенные по результатам равновесных экспериментов. . В общем, на метод геохимической термометрии вулканических пород распространяются все те ограничения, которые должны оговариваться при использовании традиционных методов петрологических интерпретаций, таких как термометрия "равновесий" вкрапленник - основная масса или оценки давлений путем проектирования валовых составов базальтов на физико-химические диаграммы, построенные по результатам равновесных экспериментов.
Назад | Оглавление| Далее
А.А. Арискин/ГЕОХИ РАН
 |
Оценка условий кристаллизации ареального вулканизма г. Терпук Срединного хребта, Камчатки.: Content |
|
 |
Оценка условий кристаллизации ареального вулканизма г. Терпук Срединного хребта, Камчатки.: Introduce |
|
 |
Бураковско-Агранозёрский расслоенный массив Заонежья: II. Строение краевой группы и оценка состава родоначальной магмы методом геохимической термометрии: Геохимическая термометрия пород краевой группы |
|
 |
Бураковско-Агранозёрский расслоенный массив Заонежья: II. Строение краевой группы и оценка состава родоначальной магмы методом геохимической термометрии: Список литературы |
|
 |
Эволюция высокоглиноземистых базальтов Ключевского вулкана (Камчатка) по данным изучения магматических включений в минералах: Аналитические методы |
|
 |
Эволюция высокоглиноземистых базальтов Ключевского вулкана (Камчатка) по данным изучения магматических включений в минералах: Методы исследования расплавных включений в минералах |
|
|
|
|
|
|


