|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Глава IX. Группы антисимметрии (шубниковские группы)
Общее определение классической симметрии включает понятие геометрического равенства, т.е. равенства объекта самому себе при симметрических преобразованиях: поворотах, отражениях, инверсии, обеспечивающих неизменность расстояний между точками объекта и соответственно углов между преобразованными прямыми и плоскостями. При этом симметрические преобразования могут быть либо без трансляций (переносов), либо трансляционными - содержать параллельные переносы. Однако, поскольку для описания ряда симметрических свойств физических объектов в трехмерном пространстве только одного геометрического равенства может оказаться недостаточно, удобно ввести четвертую переменную, имеющую определенный физический смысл: время, знак заряда, цвет, спин и т.д. Если такая переменная имеет лишь два противоположных значения, то описание может быть проведено с использованием понятия "антисимметрия" - "черно-белая" симметрия, если же значений больше двух, то с помощью понятия "многоцветная симметрия" [55, 57].
IX.1. Общие сведения
Идея антисимметрии, выдвинутая в 1929 г. немецким исследователем Г.Хеешем [ 64 ], была воплощена им в выводе классов антисимметрии. Независимо от него вывод последних был осуществлен российским кристаллографом А.В.Шубниковым в 1945 г. [51, 53]. Автором идеи "цветной" симметрии является академик Н.В.Белов [7]. Следует отметить, что уже в таком понятии классической симметрии, как "энантиоморфизм", т.е. зеркальное равенство, заложена некая противоположность свойств: правизна и левизна, т.е. идея противоположного равенства, или антиравенства. От антиравенства к антисимметрии нетрудно перейти, вспомнив, что симметрично равные фигуры могут быть либо конгруэнтными (только правыми или только левыми), либо энантиоморфными. Антисимметричные фигуры, несмотря на их геометрическое равенство, различаются какими-либо противоположными свойствами или признаками.
В качестве примеров можно привести такие дополняющие друг друга предметы с противоположными свойствами, как выпуклая медаль и вогнутый слепок с нее, капелька воды в воздухе и пузырек воздуха в воде, негатив и позитив либо пара зеркально равных фигур (см. цветную вставку, рис. 135), одна из которых окрашена в белый, а другая - в черный цвет. Для того чтобы связать между собой подобные объекты с прямо противоположными свойствами, представлений классической симметрии явно недостаточно, и поэтому удобно использовать понятие "антисимметрия", связывающее противоположные объекты, снабдив эти объекты знаками <+> и <->. Если положительные объекты считать "белыми", а отрицательные - "черными" (или наоборот), то вместо термина антисимметрия можно употребить термин черно-белая, или двухцветная, симметрия.
На рис. 135 нетрудно увидеть, что преобразование белой правой фигуры в черную левую может быть осуществлено последовательными операциями: отражением в вертикальной зеркальной плоскости симметрии (m) и "перекрашиванием" - новой операцией, называемой антиотождествлением (антитождеством) и обозначаемой 1'. Как и в случае сложных осей симметрии - зеркальных и инверсионных, включающих два симметрических преобразования, - операции коммутируют, т.е. последовательность их проведения безразлична. Такая новая комбинированная операция названа антиотражением, а соответствующий этой операции элемент симметрии - плоскостью антисимметрии, обозначаемой m' (к обозначению классической операции симметрии добавляется "штрих"). Таким образом, можно ожидать для каждой классической операции симметрии (элемента симметрии) соответствующую операцию антисимметрии (элемент симметрии): для зеркального отражения m - антиотражение m', для поворота вокруг оси n - антиповорот вокруг оси n', для инверсии в точке 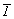 - антиинверсию - антиинверсию 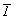 ' и для операции отождествления 1 - операция антиотождествления - антитождества 1' (операция перекрашивания - изменения какого-либо свойства на противоположное - с сохранением фигуры на месте). ' и для операции отождествления 1 - операция антиотождествления - антитождества 1' (операция перекрашивания - изменения какого-либо свойства на противоположное - с сохранением фигуры на месте).
Рассмотрим действие элементов антисимметрии на примере осей разных порядков. В случае четных осей антисимметрии (см. цветную вставку, рис. 136) наблюдается равное количество положительных (белых) и отрицательных (черных) фигур, т.е. изображенные группы антисимметрии 2', 4' и 6' содержат классические подгруппы вдвое меньшего порядка - 1, 2 и 3 соответственно. Очевидно, что дважды повторенная операция антисимметрии отвечает классической операции симметрии: (2')2 = 1, (4')2 = 2, (6')2 = 3. Показатель степени указывает на количество проведенных операций симметрии. Соответственно и группы антисимметрии - шубниковские группы (G') - имеют подгруппами классической симметрии (G) группы вдвое меньшего порядка: группа 2' в качестве классической подгруппы содержит операцию тождественности (1), группа 4' - подгруппу 2, группа 6' - подгруппу 3.
Из сказанного явствует, что вводом антитождества (переменой цвета), сопровождающего операции группы классической симметрии, получаем группу антисимметрии с классической подгруппой вдвое меньшего порядка. Снимая цвет, повышаем порядок получившейся классической группы соответственно в 2 раза по сравнению с порядком исходной классической подгруппы. Следовательно, свойствами антисимметрии могут обладать только элементы антисимметрии четных порядков, ибо в противном случае (для осей нечетных порядков) невозможны подгруппы с порядком вдвое ниже.
Например, если каждый поворот на 120o вокруг классической оси 3-го порядка сопроводить операцией перекрашивания (антитождества) 1' (рис. 137), то ось 3 одновременно окажется и простой поворотной (классической) и осью антисимметрии, т.е. в результате наложения черных и белых фигур друг на друга получим фигуры нейтрального серого цвета - фигуры физически нейтральные. Отсюда такую ось (так же, как и операцию симметрии) называют серой, или нейтральной, и обозначают 3? 1', где операция антитождества (1') присутствует как самостоятельная (!) операция. Обратим внимание на то, что введение цвета в данном случае не понизило вдвое порядок классической группы. Например, в серой группе 1' = (1, 1') каждая операция тождественности (1) сопровождается перекрашиванием - самостоятельной операцией антитождества (1').
Расширенный набор операций (элементов) симметрии - классических и антисимметрии - подчиняется общим законам взаимодействия элементов симметрии. Причем очевидно, что при однородных порождающих элементах (симметрии или антисимметрии) возникнет классический элемент (см. цветную вставку, рис. 138, а, б)1 , а при разнородных - элемент антисимметрии (рис. 138, в). Таким образом, сочетания классических операций дадут 32 классические точечные группы симметрии, подразумевающие какое-то одно - определенное - из двух возможных, но физически противоположных, свойство : "+" или "-". В таких "одноцветных" группах отсутствует операция перемены знака (цвета), поэтому в "черно-белой" терминологии они называются полярными.
Группы, в которых все операции нейтральные (серые), т.е. каждая классическая операция симметрии совпадает с аналогичной операцией антисимметрии, составляют второе семейство нейтральных, или серых, групп. Такие нейтральные группы можно получить из полярных добавлением самостоятельной операции антитождества 1' (операции перемены знака) или, что то же самое, "умножением" полярной группы G на группу второго порядка 1' = (1, 1'), при этом "умножение" на операцию 1 сохранит все операции исходной классической группы, "умножение" же на операцию 1' приведет к появлению комбинированных операций - операций антисимметрии. Отсюда порядок расширенной (серой) группы G . 1' будет вдвое больше порядка исходной полярной кристаллографической группы G. Естественно, каждой из 32 полярных групп G будет соответствовать нейтральная (серая): (G . 1'). В символе это отражается добавлением знака антитождества : 4. 1', 4mm . 1'.
При взаимодействии двух операций антисимметрии дважды повторенная операция антитождества, входящая в качестве составной части в операции антисимметрии, "погасит" перемену знака (цвета); при этом оставшиеся классические составляющие обусловят возникновение классического элемента симметрии (рис. 138, б). Поэтому цветные операции симметрии - операции антисимметрии - по аналогии с операциями классической симметрии 2-го рода не могут самостоятельно составить группу симметрии. Взаимодействие разнородных операций - классической и антисимметрии (рис. 138, в) - породит операцию антисимметрии. В результате указанных взаимодействий возникнут группы смешанной полярности - группы, в состав которых входят как классические операции, так и операции антисимметрии, за исключением антиотождествления. Следует отметить, что антитождество, отсутствующее в таких группах как самостоятельная операция, входит в операции антисимметрии, но уже в качестве их составной части.
Например, на рис. 136, б изображена фигура смешанной полярности, иллюстрирующая группу 4-го порядка - 4'. Эта группа включает 4 следующие операции:
антиповорот на 90o - (4')1,
простой поворот на 180o - (4')2 = 2,
антиповорот на 270o - (4')3 = (4')-1,
отождествление - (4')4 = 1.
При этом операция антитождества входит в состав сложных антиповоротов на 90 и 270o в качестве составляющей симметрических операций. На рис. 136 хорошо видно, что порядок классической подгруппы 2z вдвое меньше порядка исходной группы антисимметрии 4'; то же справедливо и для черно-белых групп 4-го порядка m' m' 2 и mm' 2' (рис. 138, б, в), имеющих своими классическими подгруппами второго порядка 2z и mx соответственно, и для группы 2-го порядка 1', содержащей в качестве подгруппы классическую операцию тождества (1) 1-го порядка.
Таким образом, для того чтобы получить группу антисимметрии G', нужно к классической подгруппе G добавить одну из удваивающих операций антисимметрии: 1', m', 2', 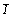 '. И обратно, любую группу антисимметрии с известным порядком (числом ее членов) можно разложить на два равноправных независимых множителя так, чтобы один из них был вдвое меньшего порядка, чем исходная группа, т.е. мог бы служить классической подгруппой, а второй - удваивающий множитель - возможной операцией антисимметрии. '. И обратно, любую группу антисимметрии с известным порядком (числом ее членов) можно разложить на два равноправных независимых множителя так, чтобы один из них был вдвое меньшего порядка, чем исходная группа, т.е. мог бы служить классической подгруппой, а второй - удваивающий множитель - возможной операцией антисимметрии.
Например, циклическая группа 6-го порядка - 61, 62, 63, 64, 65, 66 (рис. 136, а) - разлагается в прямое произведение двух множителей (3 . 2) - двух подгрупп: 3(1 = 66 , 31 = 62, 3-1 = 64 ) и 2(1 = 66, 2 = 63). Первая (3-го порядка) может служить классической подгруппой, а вторая (2-го порядка) - удваивающей группой антисимметрии: 3. 2' = 6'.
Группы 4-го порядка - 4 и 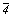 - также разлагаются на два множителя (4 = 2 . 2), один из которых является самостоятельной классической подгруппой 2-го порядка, оставшийся же множитель подгруппой не является, вне осей 4 и - также разлагаются на два множителя (4 = 2 . 2), один из которых является самостоятельной классической подгруппой 2-го порядка, оставшийся же множитель подгруппой не является, вне осей 4 и 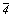 не существует и поэтому обозначается 4(mod2) и не существует и поэтому обозначается 4(mod2) и 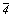 (mod2) соответственно. И именно этот множитель группы может служить удваивающей операцией (но не элементом симметрии!) групп антисимметрии: 4' = 2 . 4'(mod2), (mod2) соответственно. И именно этот множитель группы может служить удваивающей операцией (но не элементом симметрии!) групп антисимметрии: 4' = 2 . 4'(mod2), 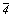 ' = 2 . ' = 2 . 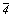 '(mod2)[55]. '(mod2)[55].
Геологический факультет МГУ
|


