|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Глава VIII. Правильные системы точек
Правильной системой точек - системой эквивалентных позиций - называется совокупность точек, полученная размножением исходной точки всеми операциями симметрии данной пространственной группы. При этом любая операция, переводящая одну точку в другую, принадлежащую этой же правильной системе, приведет к совмещению всех остальных точек данной системы, т. е. преобразует данную систему в самоё себя 1 .
Поскольку аналогами 32 точечных групп симметрии являются 230 пространственных, аналогом правильной системы точек на макроуровне можно считать простую форму - семейство граней, связанных всеми симметрическими операциями какой-либо точечной группы. И так же как грани каждой простой формы в кристаллическом многограннике подчиняются законам простых форм, в кристаллической структуре материальные частицы - атомы, ионы, молекулы - располагаются по законам, диктуемым правильными системами точек. Построение правильных систем точек и вывод компактных формул для расчета координат всех точек каждой пространственной группы было одним из самых больших достижений Е.С.Федорова.
Как число граней простой формы определяется их расположением относительно элементов симметрии точечной группы, так и количество позиций, характеризующих одну правильную систему точек, будет зависеть от положения исходной точки относительно элементов симметрии пространственной группы. Поэтому основной характеристикой правильной системы точек служит симметрия их позиций - комплекс макроэлементов симметрии, фиксирующих эти позиции, т.е. не размножающих их. Таким комплексом симметрии служит одна из 32 точечных групп, являющаяся подгруппой данной пространственной группы. Следует отметить, что элементы микросимметрии - трансляционные элементы симметрии - не фиксируют точки правильной системы в силу обязательного присутствия в них трансляционных компонент, одинаково размножающих как точки, лежащие на этих элементах, так и оказавшиеся вне их - точки общего положения (см. рис. 78). Поэтому точки, лежащие на трансляционных элементах симметрии, ничем не отличаются от точек общего положения, не фиксированных ни одним элементом симметрии. Точки общего положения - образуют общую правильную систему, все иные точки - точки на элементах макросимметрии - ими фиксируются и образуют частные правильные системы.
Элементы макросимметрии диктуют и симметрию тех частиц (атомов или их группировок), которые на них располагаются. В отличие от них трансляционные элементы симметрии не накладывают ограничений на симметрию расположенных на них частиц.
Точки общего положения, т.е. общей правильной системы, подвержены всем операциям как макро-, так и микросимметрии данной пространственной группы, и поэтому их количество, приходящееся на одну элементарную ячейку (кратность) максимально и численно равно порядку данной пространственной группы, т.е. количеству независимых операций симметрии, ее составляющих. Обратим внимание на то, что в число операций симметрии входит и ее трансляционный комплекс, задающийся определенным типом решетки Браве. Так, Р-решетка, в которой отсутствуют дополнительные трансляции, не увеличивает порядок "подрешеточного" комплекса данной группы, т.е. порядок соответствующей ей точечной группы (например, порядок группы Рmna, равный 8, соответствует порядку точечной группы mmm). Дополнительный трансляционный вектор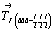 или или 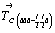 центрированной решетки удваивает порядок пространственной группы по сравнению с порядком соответствующей Р-группы, тогда как F-решетка с тремя дополнительными векторами центрированной решетки удваивает порядок пространственной группы по сравнению с порядком соответствующей Р-группы, тогда как F-решетка с тремя дополнительными векторами 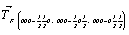 его учетверяет. его учетверяет.
Если качественным показателем правильной системы точек является симметрия позиций, то количественно степенью ее симметричности служит величина симметрии - порядок точечной подгруппы, описывающей симметрию частной позиции, т.е. ее размножающая способность. А так как величина симметрии характеризует количество точек общего положения, слившихся в одной частной позиции, она показывает и во сколько раз количество точек общей правильной системы превышает количество точек данного частного положения. Например, если симметрия позиции характеризуется точечной группой mm2, то величина симметрии данного комплекса равна 4. И по сравнению с количеством точек общего положения какой-либо пространственной группы, приходящихся на одну элементарную ячейку, точек в позиции mm2 окажется в 4 раза меньше.
Как видим, кратность любой правильной системы зависит от величины симметрии позиций ее точек - порядка точечной группы симметрии. И чем более симметрична позиция (т.е. чем больше ее величина симметрии), тем меньше ее кратность, определяемая как частное от деления порядка данной пространственной группы на ее (позиции) величину симметрии. Очевидна и обратная зависимость: произведение кратности правильной системы точек (ni) на ее величину симметрии (si) постоянно и равно кратности общей правильной системы (n), т.е. порядку пространственной группы. Данная формулировка есть суть закона А.В.Шубникова, который выражается формулой: n = ni . si [56]. Этот закон помогает получить недостающие сведения о той или иной кристаллической структуре - о расположении в ней атомов или молекул. Например, зная пространственную группу какого-либо соединения и симметрию позиций, занимаемых атомами, несложно рассчитать кратность этих позиций, а следовательно, и установить тип химической формулы и т. д.
Симметрия позиций правильной системы точек определяет еще одну ее характеристику: число степеней свободы, т.е. число направлений, перемещаясь вдоль которых, точка не размножается элементами симметрии данной позиции и продолжает ими фиксироваться (а следовательно, не меняет своей точечной симметрии).
В инвариантной (нонвариантной) системе - системе без степеней свободы - положение каждой точки строго закреплено элементами характеризующей ее симметрию точечной группы: центром инверсии (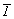 ), пересечением осей (например, 222, 32 и т.д.), пересечением оси и перпендикулярной к ней плоскости ( ), пересечением осей (например, 222, 32 и т.д.), пересечением оси и перпендикулярной к ней плоскости (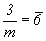 ) или только особой точкой инверсионной оси ( ) или только особой точкой инверсионной оси (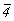 ). ).
Моновариантная система эквивалентных точек - система точек с одной степенью свободы вдоль какого-либо направления - расположена на поворотной оси симметрии любого порядка.
Система с двумя степенями свободы - дивариантная система - образована точками, расположенными на зеркальной плоскости.
Общая правильная система точек тривариантна, т.е. имеет три степени свободы. Фиксированные координаты точек инвариантной, моновариантной и дивариантной систем выражены в рациональных долях соответствующих им параметров элементарной ячейки. Не фиксированные вдоль какого-либо координатного направления (X, Y или Z) точки имеют переменные значения координат в этих направлениях. Таким образом, координаты точек, выраженные в долях параметров элементарной ячейки, являются еще одной характеристикой правильной системы. При этом если в Р-ячейке приходится приводить координаты всех точек каждой правильной системы, то в непримитивных решетках обычно прибегают к сокращенной их записи: сначала выписывают координаты узлов решетки, т.е. координаты начала и конца каждого дополнительного трансляционного вектора (например, для I-решетки - 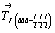 ), и затем приводят координаты лишь тех точек, которые не связаны дополнительными векторами рассматриваемой решетки. Для получения полного списка координат всех точек данной системы достаточно к приведенным координатам каждой точки добавить указанные в начале координаты узлов векторов центрированной решетки. Например, если точка имела координаты xyz, то, размноженная вектором ), и затем приводят координаты лишь тех точек, которые не связаны дополнительными векторами рассматриваемой решетки. Для получения полного списка координат всех точек данной системы достаточно к приведенным координатам каждой точки добавить указанные в начале координаты узлов векторов центрированной решетки. Например, если точка имела координаты xyz, то, размноженная вектором 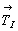 , она получит следующие координаты: , она получит следующие координаты: 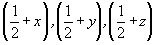 . Это позволяет сократить количество координат точек в соответствующее количеству дополнительных векторов раз. . Это позволяет сократить количество координат точек в соответствующее количеству дополнительных векторов раз.
Рассмотрим различные правильные системы точек на примере пространственных групп Рmna, 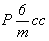 и и 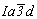 . .
Пространственная группа Рmna (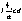 ) )
На графике пространственной группы Рmna (рис. 129) хорошо видно, что кроме общей - тривариантной - правильной системы (А) есть все типы частных: дивариантная (В) - на зеркальной плоскости mx, две моновариантные (С) - на осях 2-го порядка 2x и 2y и нонвариантная (D) - в точке пересечения 2x и mx, т.е. в центре инверсии.
Общая правильная система точек
Поскольку точки общей правильной системы не фиксированы относительно элементов симметрии данной пространственной группы и, следовательно, имеют три степени свободы вдоль трех координатных направлений, то любое изменение их координат не приводит к изменению кратности системы. Каждая координата, выраженная в долях элементарной ячейки, откладывается (измеряется) от начала координат вдоль соответствующей координатной оси. Координата + z показывает высоту точки над (под) нулевым уровнем (плоскостью чертежа). Однако на графике рядом с точкой оставляется лишь знак этой координаты (+ или - ), ибо абсолютного значения вертикальной координаты в проекции пространственной группы на плоскость чертежа не видно.
Для получения всех точек общей правильной системы можно группу симметрии разложить на независимые подгруппы - сомножители. При этом естественно сначала на исходную точку подействовать элементами симметрии 1-го рода, получив таким образом все конгруэнтно равные точки, т.е. половину всего количества общих точек, затем, использовав простейшую и коммутирующую с другими операцию "отражения" в точке - инверсию, получить оставшуюся половину энантиоморфных точек этой системы. Однако на практике часто проще действовать подрешеточными - порождающими - элементами симметрии группы. На заключительном этапе получения всех точек системы необходимо включить в действие трансляционный комплекс данной группы симметрии. При этом в непримитивных решетках число точек правильной системы увеличится в соответствии с числом дополнительных трансляционных векторов.
На графике данной голоэдрической группы Pmna для получения всех точек общего положения (а их количество - кратность - в Р-решетке соответствует порядку точечной группы mmm, равному 8), достаточно подействовать на исходную точку (xyz) последовательно всеми независимыми плоскостями симметрии (mx, ny и az), обозначенными в символе данной пространственной группы, посчитав их порождающими элементами симметрии. Порожденные же этими плоскостями оси 2-го порядка и центры инверсии можно использовать для проверки правильности полученного результата.
Итак, исходная точка А1 (см. рис. 129) с координатами xyz после отражения в зеркальной плоскости mx займет энантиоморфное положение А2 с координатами 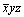 (на чертеже такую энантиоморфную точку отмечают запятой): (на чертеже такую энантиоморфную точку отмечают запятой):
xyz (А1) . my --> 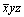 (А2). (А2).
Дальнейшее отражение полученных двух точек в плоскости ny переведет каждую из них в энантиоморфное положение:
xyz (A1). ny --> 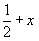 , , 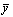 , , 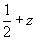 (A3), (A3),
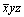 (A2) . ny --> (A2) . ny --> 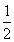 - x, - x, 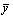 , , 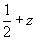 (A4) (точка А4 при этом потеряет запятую). (A4) (точка А4 при этом потеряет запятую).
Последовательные отражения исходной точки в двух взаимно перпендикулярных плоскостях симметрии mx и ny равносильны повороту вокруг результирующей оси 21(z). Действительно, каждая пара конгруэнтных точек - А1 и А4, А2 и А3 - связаны поворотами вокруг осей 21, расположенных в позициях 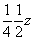 и и 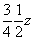 соответственно. Отражение полученных четырех точек в плоскости az, расположенной на высоте соответственно. Отражение полученных четырех точек в плоскости az, расположенной на высоте 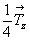 относительно выбранного начала координат, удвоит их количество: относительно выбранного начала координат, удвоит их количество:
xyz (A1) . az --> 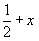 , y, , y, 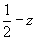 (A5), (A5),
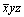 (A2) . az --> (A2) . az --> 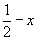 , y, , y, 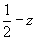 (A6), (A6),
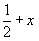 , , 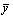 , , 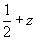 (A3) . az --> (A3) . az --> 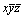 (A7), (A7),
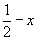 , , 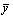 , , 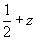 (A4) . az --> (A4) . az --> 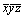 (A8). (A8).
Для того чтобы облегчить получение координат точек при отражении в горизонтальной плоскости az, удобно воспользоваться схемой, где вертикальный параметр с без сокращения располагается в плоскости чертежа (в проекции на плоскость yz) (рис. 130, в).
Из рис. 130 видно, что как плоскость az, так и ось 2y, отстоящие на 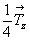 от нулевого уровня, соответствующего началу от нулевого уровня, соответствующего началу  координат, переведут исходную точку с третьей координатой 2 +z на уровень координат, переведут исходную точку с третьей координатой 2 +z на уровень 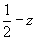 и соответственно точку с координатой и соответственно точку с координатой 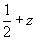 - на высоту - z. Если же элемент симметрии (например, центр инверсии) находится на нулевом уровне (z = 0), то координата +z переведется в - z и точка с координатой - на высоту - z. Если же элемент симметрии (например, центр инверсии) находится на нулевом уровне (z = 0), то координата +z переведется в - z и точка с координатой 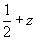 окажется на высоте окажется на высоте 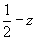 , так как она будет отражена в центре инверсии, расположенном на середине вертикальной трансляции, т.е. на высоте , так как она будет отражена в центре инверсии, расположенном на середине вертикальной трансляции, т.е. на высоте 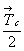 (см. с. 58). (см. с. 58).
Обратим внимание на то, что результатом отражения в трех взаимно перпендикулярных плоскостях будет операция "отражения" в центре инверсии (операция инверсии в точке). Поэтому из четырех точек (А1-4), полученных отражением в плоскостях mx и ny, просто получить оставшиеся четыре (А5-8), подействовав на них центром инверсии, т.е. поменяв знаки их координат на обратные (при условии, что центр инверсии находится в начале координат). Таким образом, знание закономерностей изменения координат при той или иной операции симметрии (см. с. 20) поможет правильно записать координаты точек и проверить результат действия этого элемента симметрии, даже не обращаясь к рисунку.
Частные правильные системы точек
Наиболее симметричными в пространственной группе Рmna являются нонвариантные правильные системы точек с симметрией 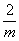 (одна из них обозначена на рис. 129 буквой D). Величина симметрии данной позиции (равная 4) позволяет легко вычислить ее кратность как частное от деления порядка пространственной группы на эту величину симметрии (8 : 4 = 2). Восемь позиций D с симметрией (одна из них обозначена на рис. 129 буквой D). Величина симметрии данной позиции (равная 4) позволяет легко вычислить ее кратность как частное от деления порядка пространственной группы на эту величину симметрии (8 : 4 = 2). Восемь позиций D с симметрией 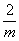 в данной пространственной группе разбиваются на 4 независимые друг от друга пары, позиции в каждой из которых связаны соответствующими операциями симметрии. Поэтому задание атома в одну из позиций не приведет к появлению такого атома в остальных трех. Отметим, что любая из указанных позиций с симметрией в данной пространственной группе разбиваются на 4 независимые друг от друга пары, позиции в каждой из которых связаны соответствующими операциями симметрии. Поэтому задание атома в одну из позиций не приведет к появлению такого атома в остальных трех. Отметим, что любая из указанных позиций с симметрией 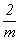 может быть использована в качестве начала координат данной пространственной группы. может быть использована в качестве начала координат данной пространственной группы.
Комплекс элементов симметрии данной подгруппы (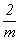 ), характеризующий симметрию рассматриваемой позиции, четко ее фиксирует, лишая степеней свободы. Это отражается на координатах точек, выраженных постоянными величинами, в данном случае 000. Так как исходная точка (000) элементами симметрии 2x и mx не размножается, то переход ко второй точке этой системы может быть осуществлен добавлением какого-либо удваивающего элемента симметрии, не содержащегося в рассматриваемом комплексе. Ибо добавление любого из них к точечной подгруппе ), характеризующий симметрию рассматриваемой позиции, четко ее фиксирует, лишая степеней свободы. Это отражается на координатах точек, выраженных постоянными величинами, в данном случае 000. Так как исходная точка (000) элементами симметрии 2x и mx не размножается, то переход ко второй точке этой системы может быть осуществлен добавлением какого-либо удваивающего элемента симметрии, не содержащегося в рассматриваемом комплексе. Ибо добавление любого из них к точечной подгруппе 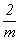 приведет к исходной пространственной группе Pnma. Например, подействовав на исходную точку (D1) с координатами 000 плоскостью ny, получим точку (D2) с координатами приведет к исходной пространственной группе Pnma. Например, подействовав на исходную точку (D1) с координатами 000 плоскостью ny, получим точку (D2) с координатами 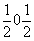 . К тому же результату приведет действие и винтовой оси 21 в позиции . К тому же результату приведет действие и винтовой оси 21 в позиции 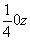 и т.д. и т.д.
В списке правильных систем точек, характеризующих пр. гр. Рnma, приводятся все 4 неэквивалентные между собой позиции с симметрией 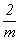 , отличающиеся лишь своими координатами (см. рис. 129). , отличающиеся лишь своими координатами (см. рис. 129).
Моновариантные позиции в данной группе расположены на поворотных осях симметрии 2x и 2y . Каждая из них имеет одну степень свободы вдоль координатной оси X или Y, и поэтому, соответствующая каждой из этих осей координата будет переменной величиной.
Исходная точка (C1), принадлежащая одной из моновариантных систем, расположенная на оси 2y , приподнятой над нулевым уровнем на 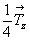 , будет характеризоваться следующими координатами: , будет характеризоваться следующими координатами: 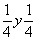 . Подействовав на нее независимыми плоскостями, например ny и az, получим количество точек (4), отвечающее кратности данной системы: . Подействовав на нее независимыми плоскостями, например ny и az, получим количество точек (4), отвечающее кратности данной системы:
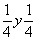 (C1) . ny --> (C1) . ny --> 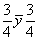 (C2), (C2),
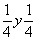 (C1) . az --> (C1) . az --> 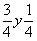 (C3), (C3),
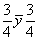 (C2) . az --> (C2) . az --> 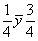 (C4). (C4).
Если в качестве одного из удваивающих элементов симметрии использовать удобный для записи координат центр инверсии в позиции 000, то вторым удваивающим элементом симметрии не может быть плоскость ny, ибо она порождена взаимодействием этого центра с подгруппой 2y, характеризующей данную моновариантную позицию. Поэтому, задавая новые элемент симметрии, необходимо следить за тем, чтобы он не оказался порожденным уже заданными операциями симметрии. В данном случае помимо центра инверсии можно использовать плоскости mx, az, ось 2x и т.д. Другие моновариантные позиции (например, с координатами x00 и 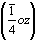 ) отличаются от только что рассмотренной моновариантной позиции ) отличаются от только что рассмотренной моновариантной позиции 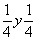 лишь координатами (см. рис. 129, 131, б). лишь координатами (см. рис. 129, 131, б).
Величина симметрии единственной в пр. гр. Pnma дивариантной позиции (B) - позиции на зеркальной плоскости mx с двумя степенями свободы - равна 2, что уменьшает ее кратность вдвое по сравнению с кратностью общей правильной системы (8 : 2 = 4). Поскольку плоскость m перпендикулярна оси X , то расположенная на ней исходная точка имеет две переменные координаты вдоль двух координатных осей - в данном случае Y и Z: 0yz. Точка с такими координатами плоскостью m не размножается - на неё действуют лишь независимые плоскости ny и az:
0yz (B1) . ny --> 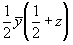 (B2), (B2),
0yz (B1) . az --> 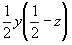 (B3), (B3),
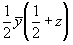 (B2) . az --> (B2) . az --> 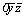 (B4). (B4).
К аналогичному результату придем, если на исходную точку подействуем осями 2-го порядка, при этом "работать" будут лишь две из них (например, 2x и 2y), так как третья - результирующая 21(z) = mx . ny - к новым позициям точек не приведет.
Вариант использования центра инверсии в позиции 000 с последующим поворотом вокруг оси 2-го порядка отвергает результирующую в этом случае ось 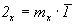 . .
Координаты точек легко получить, используя график соответствующей пространственной группы. Однако, зная закономерности изменения координат точек под действием того или иного элемента симметрии (см. с. 20), можно их рассчитать и аналитически. Это не вызывает затруднений, если данный размножающий элемент симметрии проходит через начало координат. Например, ось 2x переведет точку xyz в положение 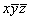 и т.д. Если же размножающий элемент симметрии не проходит через начало координат, то прежде, чем действовать на какую-либо точку этим элементом симметрии, надо временно изменить начало координат, перенеся его на этот элемент, записать координаты точки относительно выбранного нового начала, затем произвести заданную элементом симметрическую операцию и уже после этого координаты полученной точки пересчитать к старому началу координат. Например, ось 2y в пр. гр. Pmna занимает позицию и т.д. Если же размножающий элемент симметрии не проходит через начало координат, то прежде, чем действовать на какую-либо точку этим элементом симметрии, надо временно изменить начало координат, перенеся его на этот элемент, записать координаты точки относительно выбранного нового начала, затем произвести заданную элементом симметрическую операцию и уже после этого координаты полученной точки пересчитать к старому началу координат. Например, ось 2y в пр. гр. Pmna занимает позицию 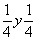 (см. рис. 129). Перенеся начало координат на эту ось, т.е. в точку с координатами (см. рис. 129). Перенеся начало координат на эту ось, т.е. в точку с координатами 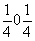 , пересчитываем координаты (xyz) исходной точки: xyz --> ( , пересчитываем координаты (xyz) исходной точки: xyz --> (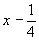 )y( )y(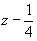 ), тем самым определяя ее положение в новой координатной системе. Далее, поворот точки с новыми координатами вокруг оси 2y, которая в новой координатной системе заняла положение (0y0), приведет к позиции ( ), тем самым определяя ее положение в новой координатной системе. Далее, поворот точки с новыми координатами вокруг оси 2y, которая в новой координатной системе заняла положение (0y0), приведет к позиции (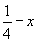 )y( )y(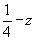 ). Возвратившись к исходному положению оси 2y ( ). Возвратившись к исходному положению оси 2y (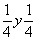 ), а следовательно, к старой координатной системе, получим точку с координатами ( ), а следовательно, к старой координатной системе, получим точку с координатами (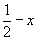 )y( )y(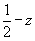 ) = ( ) = (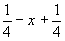 ) y ( ) y (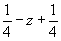 ), что можно подтвердить и графически (см. рис. 129) . ), что можно подтвердить и графически (см. рис. 129) .
В Интернациональных таблицах [71-73] в характеристику каждой правильной системы точек пространственной группы помимо кратности (количества позиций в элементарной ячейке) и ее симметрии входит обозначение Уайкоффа (Wyckoff) - буквенное обозначение (последовательность латинского алфавита отвечает увеличению кратности позиции). Самая симметричная позиция - позиция с минимальной кратностью - обозначается буквой "а" (рис. 131). Кроме этого, обязательно указывается символ данной пространственной группы в обозначении Шенфлиса, ее порядковый номер и соответствующая точечная группа симметрии. Таким образом, в символе Уайкоффа независимые позиции даже с одинаковыми характеристиками, различающиеся лишь координатами, обозначаются разными буквами.
Пространственная группа 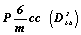
Гексагональную голоэдрическую пространственную группу 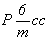 определяют три независимые плоскости симметрии, две из которых - координатная и апофемальная - вертикальны и располагаются одна относительно другой под углом 30o , третья плоскость mz им перпендикулярна. Порядок пространственной группы, равный 24, соответствует в Р-решетке кратности общей правильной системы (А), т.е. порядку точечной группы гексагональной голоэдрии (рис. 132). При описании характеристик правильных систем в пространственных группах гексагональной сингонии определенные трудности возникают при получении координат точек. определяют три независимые плоскости симметрии, две из которых - координатная и апофемальная - вертикальны и располагаются одна относительно другой под углом 30o , третья плоскость mz им перпендикулярна. Порядок пространственной группы, равный 24, соответствует в Р-решетке кратности общей правильной системы (А), т.е. порядку точечной группы гексагональной голоэдрии (рис. 132). При описании характеристик правильных систем в пространственных группах гексагональной сингонии определенные трудности возникают при получении координат точек.
Для получения точек общего положения число, соответствующее порядку данной группы, удобно разложить на сомножители, каждый из которых будет порядком соответствующей подгруппы: 24 = 1 . 3 . 2 . 2 . 2, и подействовать на исходную точку симметрическими операциями, порядок которых соответствует этим числам: в рассматриваемом случае - осью 6 = 3 . 2, т.е. сначала осью 3-го, а затем 2-го порядка. В результате этого получим 6 конгруэнтных точек. Последующий поворот вокруг горизонтальной координатной оси 2 удвоит количество точек (6 ?. 2 = 12), в результате будут получены все 12 конгруэнтных точек. Последующая операция инверсии в точке приведет к такому же количеству (12) точек энантиоморфных. В итоге будем иметь все 24 (12 . 2) точки общего положения (рис. 132).
Для размножения исходной точки осью 3-го порядка и записи координат полученных точек удобно воспользоваться третьей горизонтальной координатной осью U. А так как при вращении вокруг оси 3, расположенной в начале координат, меняются лишь положения точек относительно трех горизонтальных осей X, Y и U при неизменной координате вдоль оси Z (рис. 133, а), соответствующие им координаты легко получить круговой перестановкой ( - знак круговой перестановки), записав предварительно координаты исходной точки xyz в четырехосной системе - xyuz (где x, y, u показывают, на какую долю соответствующего горизонтального параметра элементарной ячейки следует продвинуться, чтобы оказаться в заданной точке): - знак круговой перестановки), записав предварительно координаты исходной точки xyz в четырехосной системе - xyuz (где x, y, u показывают, на какую долю соответствующего горизонтального параметра элементарной ячейки следует продвинуться, чтобы оказаться в заданной точке):
xyz (1) --> xy0z  y0xz (2), 0xyz (3). y0xz (2), 0xyz (3).
Для возвращения от четырехосной к трехосной системе координат следует избавиться от лишней координаты по третьей горизонтальной оси U, предварительно обратив ее в нуль [3, 18]. Для этого следует вычесть соответственно из всех трех координат по горизонтальным осям значение координаты по оси U, что оставит, как это видно из рис. 133, а, точку на месте. В результате получим точки со следующими координатами (рис. 133, б):
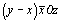 (2) --> (2) -->  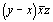 и и 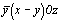 (3) --> (3) --> 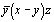 . .
Дальнейший поворот вокруг оси 2(00z), входящей в качестве подгруппы в группу 6, изменит знаки первых двух координат точек на противоположные, оставив неизменной третью координату. В результате получим еще 3 точки, конгруэнтные исходной:
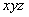 (1) (1) 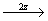 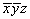 (4), (4),
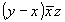 (2) (2) 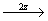 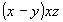 (5), (5),
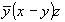 (3) (3) 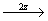 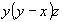 (6). (6).
У каждой из перечисленных выше шести точек после поворота вокруг горизонтальной координатной оси 2u (см. рис. 132) поменяются местами первые две координаты и изменится на противоположный знак третьей. Однако, поскольку ось 2u расположена на высоте 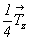 , все размноженные ею конгруэнтные точки окажутся на высоте , все размноженные ею конгруэнтные точки окажутся на высоте 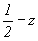 : :
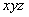 (1) (1) 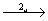 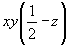 (7), (7),
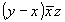 (2) (2) 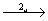 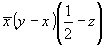 (8), (8),
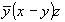 (3) (3) 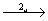 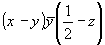 (9), (9),
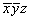 (4) (4) 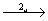 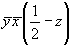 (10), (10),
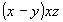 (5) (5) 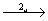 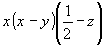 (11), (11),
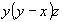 (6) (6) 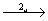 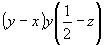 (12). (12).
 Далее, "отразив" 12 точек в центре инверсии и изменив этим знаки их координат на противоположные, получим еще 12 точек, энантиоморфных исходным, т.е. все 24 искомые точки общего положения (см. рис. 132): Далее, "отразив" 12 точек в центре инверсии и изменив этим знаки их координат на противоположные, получим еще 12 точек, энантиоморфных исходным, т.е. все 24 искомые точки общего положения (см. рис. 132):
 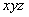 (1) (1) 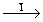 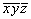 (13), (13),
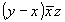 (2) (2)  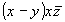 (14), и т.д. (14), и т.д.
К такому же результату можно было прийти, использовав вместо инверсии в точке операцию симметрии также 2-го порядка - отражение в горизонтальной координатной плоскости, что тем более удобно, так как плоскость расположена на нулевом уровне.
На графике пр. гр. 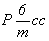 все 12 полученных вначале точек окажутся расположенными над (или под) энантиоморфными им точками. Такие попадающие в проекции xy в одну позицию точки обозначаются перечеркнутым кружком, одна половина которого символизирует точку на высоте +z, другая - ей энантиоморфную на высоте - z. Фактически верхние (+z) и нижние (- z) точки связаны между собой отражением в горизонтальной плоскости mz. Зная закономерности изменения координат точек под действием той или иной симметрической операции, можно легко охарактеризовать и координаты точек десяти принципиально различных по симметрии частных правильных систем рассматриваемой пространственной группы: все 12 полученных вначале точек окажутся расположенными над (или под) энантиоморфными им точками. Такие попадающие в проекции xy в одну позицию точки обозначаются перечеркнутым кружком, одна половина которого символизирует точку на высоте +z, другая - ей энантиоморфную на высоте - z. Фактически верхние (+z) и нижние (- z) точки связаны между собой отражением в горизонтальной плоскости mz. Зная закономерности изменения координат точек под действием той или иной симметрической операции, можно легко охарактеризовать и координаты точек десяти принципиально различных по симметрии частных правильных систем рассматриваемой пространственной группы: 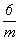 , 6, 622, , 6, 622, 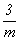 , 32, 3, , 32, 3, 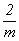 , 222, 2, m, учитывая, что точки каждой из перечисленных систем связаны операциями симметрии, не входящими в группу симметрии позиции. Например, если точка занимает позицию, характеризующуюся точечной группой 6-го порядка (32), то на точку будут действовать все оставшиеся симметрические операции группы , 222, 2, m, учитывая, что точки каждой из перечисленных систем связаны операциями симметрии, не входящими в группу симметрии позиции. Например, если точка занимает позицию, характеризующуюся точечной группой 6-го порядка (32), то на точку будут действовать все оставшиеся симметрические операции группы 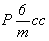 , т.е. два элемента симметрии 2-го порядка 1-го (одна из апофемальных осей 2-го порядка) и 2-го (центр инверсии или горизонтальная плоскость) рода. В результате исходная точка с координатами , т.е. два элемента симметрии 2-го порядка 1-го (одна из апофемальных осей 2-го порядка) и 2-го (центр инверсии или горизонтальная плоскость) рода. В результате исходная точка с координатами 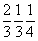 под действием координатной оси 2-го порядка 2 под действием координатной оси 2-го порядка 2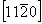 на высоте на высоте 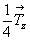 займет положение займет положение 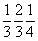 . Затем обе точки, будучи отраженными в центре инверсии с координатами . Затем обе точки, будучи отраженными в центре инверсии с координатами 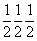 , займут положения , займут положения 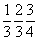 и и 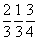 соответственно. соответственно.
Пространственная группа 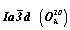
Для получения всех точек общего положения в пространственной группе 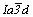 (см. рис. 114) следует порядок группы (96) разложить на сомножители (старшие независимые подгруппы) таким образом (96 = 4 . 3 . 2 . 2 . 2), чтобы, воспользовавшись соответствующими этим сомножителям симметрическими операциями - подгруппами данной группы, было удобно получить координаты размноженных точек. При этом необходимо следить за тем, чтобы порядок сомножителей соответствовал реальному элементу симметрии, присутствующему в данной группе. (см. рис. 114) следует порядок группы (96) разложить на сомножители (старшие независимые подгруппы) таким образом (96 = 4 . 3 . 2 . 2 . 2), чтобы, воспользовавшись соответствующими этим сомножителям симметрическими операциями - подгруппами данной группы, было удобно получить координаты размноженных точек. При этом необходимо следить за тем, чтобы порядок сомножителей соответствовал реальному элементу симметрии, присутствующему в данной группе.
Например, порядок группы 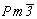 раскладывается на сомножители следующим образом: 24 = 4 . 3 . 2. Приписывая каждому из сомножителей определенную операцию симметрии, убеждаемся в том, что в данной группе нет реального элемента симметрии (подгруппы) 4-го порядка. Следовательно, сомножитель 4 необходимо представить двумя операциями 2-го порядка. В итоге получаем: 24 = = 3 . 2. 2 . 2. Учитывая некоммутативность операции 3 (для точек частного положения) и коммутативность операции инверсии в точке с остальными операциями пространственной группы, выстраиваем их в следующем порядке: 2z , 2x , 3[111] , раскладывается на сомножители следующим образом: 24 = 4 . 3 . 2. Приписывая каждому из сомножителей определенную операцию симметрии, убеждаемся в том, что в данной группе нет реального элемента симметрии (подгруппы) 4-го порядка. Следовательно, сомножитель 4 необходимо представить двумя операциями 2-го порядка. В итоге получаем: 24 = = 3 . 2. 2 . 2. Учитывая некоммутативность операции 3 (для точек частного положения) и коммутативность операции инверсии в точке с остальными операциями пространственной группы, выстраиваем их в следующем порядке: 2z , 2x , 3[111] , 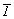 . Далее используем приведенные выше рекомендации для получения точек общего положения пр. гр. . Далее используем приведенные выше рекомендации для получения точек общего положения пр. гр. 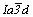 . Вначале, подействовав операциями симметрии 1-го рода: осью 41(z), диагональной осью 2d и осью 3-го порядка, получим 24 конгруэнтные точки. Затем, добавив инверсию в точке, - еще 24 энантиоморфные им точки, и в заключение, введя дополнительный вектор объемноцентрированной решетки . Вначале, подействовав операциями симметрии 1-го рода: осью 41(z), диагональной осью 2d и осью 3-го порядка, получим 24 конгруэнтные точки. Затем, добавив инверсию в точке, - еще 24 энантиоморфные им точки, и в заключение, введя дополнительный вектор объемноцентрированной решетки 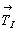 , запишем координаты всех 96 точек общего положения (рис. 134). , запишем координаты всех 96 точек общего положения (рис. 134).
1. Если бы ось 4-го порядка была поворотной и проходила через начало координат, то исходная точка размножилась бы ею по следующему закону: 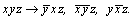 Но поскольку в данной пространственной группе винтовая ось 41(z) смещена на Но поскольку в данной пространственной группе винтовая ось 41(z) смещена на 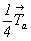 , то, прежде чем ею действовать, надо привести координаты исходной точки к новому началу координат, взятому на этой оси в позиции , то, прежде чем ею действовать, надо привести координаты исходной точки к новому началу координат, взятому на этой оси в позиции 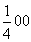 , вычтя из координаты x точки значение этой же координаты для оси, фиксирующей новое начало координат. В результате получим новые координаты точки (1) - ( , вычтя из координаты x точки значение этой же координаты для оси, фиксирующей новое начало координат. В результате получим новые координаты точки (1) - (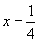 )уz - и только после этого повернем ее вокруг оси 41, имея при этом в виду, что к координате z при каждом повороте будет добавляться трансляционная составляющая этой оси )уz - и только после этого повернем ее вокруг оси 41, имея при этом в виду, что к координате z при каждом повороте будет добавляться трансляционная составляющая этой оси 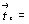 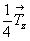 : :
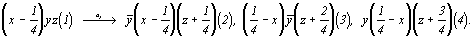 (1) (1) 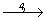 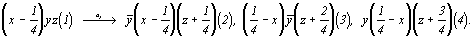 (2), (2), 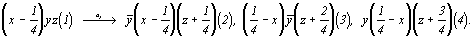 (3), (3), 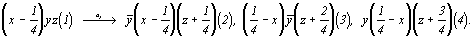 (4) (4)
Приведя полученные координаты к исходному началу, т.е. прибавив 1/4 к координате x, получим
xyz (1)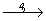 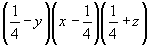 (2), (2), 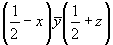 (3), (3), 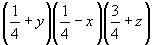 (4). (4).
При этом точку (2), оказавшуюся за пределами исходной элементарной ячейки, трансляцией 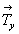 вносим в пределы ячейки. В результате ее координаты запишутся следующим образом: вносим в пределы ячейки. В результате ее координаты запишутся следующим образом:
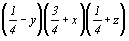 . .
2. Далее каждую из четырех точек (1- 4) повернем вокруг диагональной оси 2d[110], сдвинутой относительно начала координат на 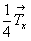 и и 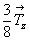 . И вновь, прежде чем подействовать этой осью, следует, предварительно перенеся начало координат в позицию . И вновь, прежде чем подействовать этой осью, следует, предварительно перенеся начало координат в позицию 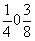 , сообщить точкам новые координаты и затем, подействовав на них осью 2d , вернуться к прежней системе координат: , сообщить точкам новые координаты и затем, подействовав на них осью 2d , вернуться к прежней системе координат:
| Координаты исходной точки в старой координатной системе |
Координаты точки координатной системе |
Координаты в новой точки, размноженной осью 2d, в новой координатной системе |
Координаты точки, размноженной осью 2d, в старой координатной системе |
 |
3. Для размножения осью 3-го порядка (3[111]) используем круговую перестановку координат каждой из восьми полученных ранее точек:
xyz (1)  yzx (9), zxy (10); yzx (9), zxy (10);
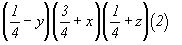 (2) (2)  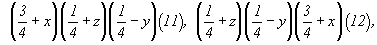 (11), (11), 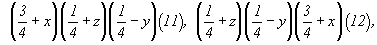 (12), (12),
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
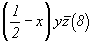 (8) (8)  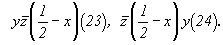 (23), (23), 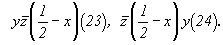 (24). (24).
4. Подействовав на полученные таким образом 8 . 3 = 24 конгруэнтные точки центром инверсии 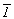 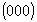 , будем иметь такое же количество им энантиоморфных: , будем иметь такое же количество им энантиоморфных:
xyz (1) 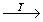 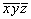 (25), (25),
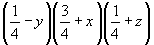 (2) (2) 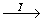 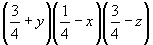 (26), (26),
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
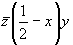 (24) (24) 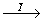 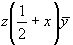 (48). (48).
В результате придем к 48 точкам, не связанным между собой трансляцией I-решетки.
5. Заключительный перенос вектором 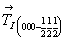 даст недостаю-щую половину точек: даст недостаю-щую половину точек:
xyz (1) 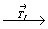 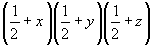 (49), (49),
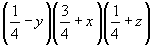 (2) (2) 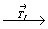 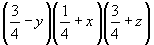 (50), (50),
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
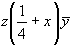 (48) (48) 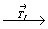 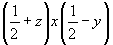 (96). (96).
Как видим, даже не прибегая к проекции, можно получить координаты всех 96 точек общего положения.
На практике удобно, использовав в качестве первой симметрической операции поворот вокруг оси 3-го порядка, получить 3 связанные ею точки. И, соединив их прямыми, начертить треугольник, который затем легко, как один материальный объект, размножить всеми порождающими элементами симметрии, в данном случае плоскостями симметрии. В результате получим график с нанесенными на него точками общего положения (см. рис. 134) 3.
Если при получении точек общего положения в конечном итоге безразлично, в каком порядке производить симметрические операции (так как они коммутируют), то, задав точку частного положения, необходимо следить за тем, чтобы вводимая симметрическая операция не оказалась уже задействованной в качестве результирующей предыдущих операций.
Например, в пр. гр. 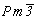 все 12 точек частной правильной системы с симметрией m можно получить, подействовав на исходную точку с координатами x0z сначала осью 2z, затем осью 3[111] и в заключение центром инверсии: все 12 точек частной правильной системы с симметрией m можно получить, подействовав на исходную точку с координатами x0z сначала осью 2z, затем осью 3[111] и в заключение центром инверсии:
x0z (1) 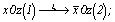 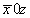 (2); (2);
x0z (1)  zx0 (3), 0zx (4); zx0 (3), 0zx (4);
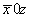 (2) (2)  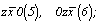 (5), (5), 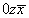 (6); (6);
x0z (1) 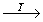 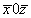 (7); (7);
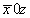 (2) (2) 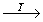 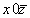 (8); (8);
zx0 (3) 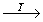 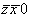 (9); (9);
0zx (4) 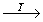 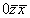 (10); (10);
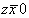 (5) (5) 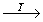 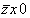 (11); (11);
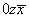 (6) (6)  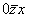 (12). (12).
Из операций 2-го рода предпочтительна инверсия, особенно если центр инверсии совпадает с началом координат (при этом меняются знаки координат точек на противоположные). Однако на точки частного положения нельзя действовать элементами симметрии, сопряженными с теми, на которых расположена точка. Например, в рассматриваемом случае (пр. гр. 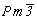 ) на точку с координатами x0z, расположенную на плоскости my, нельзя действовать осью 2y совместно с ) на точку с координатами x0z, расположенную на плоскости my, нельзя действовать осью 2y совместно с 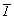 (так как (так как 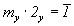 ). Кроме того, в данном случае операции оси 3-го порядка не коммутируют с операциями осей 2-го порядка, так как точка x0z, будучи размноженной осью 3[111] , окажется в позициях на плоскостях mx и mz. Поэтому дальнейшее одновременное введение оси 2-го порядка и центра инверсии (например, 2z и ). Кроме того, в данном случае операции оси 3-го порядка не коммутируют с операциями осей 2-го порядка, так как точка x0z, будучи размноженной осью 3[111] , окажется в позициях на плоскостях mx и mz. Поэтому дальнейшее одновременное введение оси 2-го порядка и центра инверсии (например, 2z и 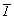 ) приведет к одной и той же позиции: ) приведет к одной и той же позиции:
x0z (1)  zx0 (2), 0zx (3); zx0 (2), 0zx (3);
zx0 (2) 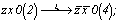 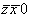 (4); (4);
zxo (2) 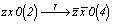 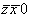 (4) (4) и т.д. и т.д.
Геологический факультет МГУ
|


