|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IX.2. Вывод точечных групп антисимметрии - групп смешанной полярности
Вывод всех точечных групп антисимметрии, как было показано выше, можно осуществить двумя путями: либо к точечным группам симметрии, принятым за классические подгруппы, добавить удваивающие элементы антисимметрии, либо в каждой из 32 точечных групп рассмотреть все возможные комбинации простых элементов и элементов антисимметрии.
В качестве примера рассмотрим вывод всех групп антисимметрии, подчиненных (изоморфных, см. с. 29) точечным группам mmm, 222,  , , 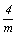 , ,  , ,  , , 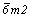 , 23 и , 23 и 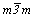 . .
mmm = 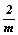   - группа 8-го порядка с тремя независимыми плоскостями симметрии (mx . my = 2z , mz независима) создает возможность вывода групп антисимметрии двумя различными путями. - группа 8-го порядка с тремя независимыми плоскостями симметрии (mx . my = 2z , mz независима) создает возможность вывода групп антисимметрии двумя различными путями.
1. Выписав подгруппы 4-го порядка (в два раза меньшего, чем порядок рассматриваемой группы): 222, mm2 и 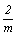 , добавляем к каждой из них какой-либо удваивающий элемент антисимметрии: , добавляем к каждой из них какой-либо удваивающий элемент антисимметрии: 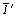 , m' или 2'. При этом количество групп антисимметрии будет соответствовать количеству выделенных классических подгрупп (см. цветную вставку, рис. 139): , m' или 2'. При этом количество групп антисимметрии будет соответствовать количеству выделенных классических подгрупп (см. цветную вставку, рис. 139):
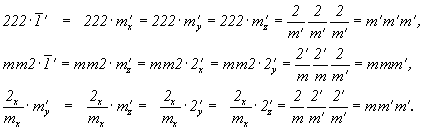
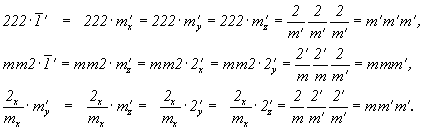
2. К тому же результату можно прийти, "зацветив" по-разному порождающие элементы симметрии исходной точечной группы, приняв за таковые три взаимно перпендикулярные плоскости симметрии. При этом элементом антисимметрии может быть одна, две или все три исходные плоскости. И поскольку все три плоскости равноправны, получим три варианта групп антисимметрии (рис. 139):
m' mm = 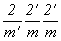 (группа с цветным центром инверсии и (группа с цветным центром инверсии и
классической подгруппой mm2(= 2mm));
m' m' m = 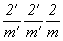 (центр инверсии простой, классическая (центр инверсии простой, классическая
подгруппа 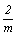 ); );
m' m' m' = 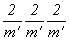 (центр инверсии цветной, классическая (центр инверсии цветной, классическая
подгруппа 222).
Развернутые символы выведенных групп антисимметрии 8-го порядка демонстрируют равное число в них операций антисимметрии и классической симметрии. Так, для группы 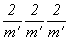 четырем операциям антисимметрии - mx', my', mz', четырем операциям антисимметрии - mx', my', mz',  - соответствуют четыре классические операции - 2x , 2y , 2z , 1, образующие классическую подгруппу в два раза меньшего порядка по сравнению с исходной группой антисимметрии. - соответствуют четыре классические операции - 2x , 2y , 2z , 1, образующие классическую подгруппу в два раза меньшего порядка по сравнению с исходной группой антисимметрии.
222 - группа 4-го порядка с классической подгруппой вдвое меньшего порядка (2). Поскольку все оси 2-го порядка в этой группе взаимосвязаны (любые две порождают третью) и топологически неразличимы, то единственный вариант группы антисимметрии - 22' 2' (= 2' 2' 2 = 2' 22' ).
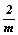 - группа 4-го порядка, каждая из подгрупп 2-го порядка которой (2, m, - группа 4-го порядка, каждая из подгрупп 2-го порядка которой (2, m, 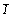 ) может быть "зацвечена" или стать классической подгруппой. Отсюда имеем три варианта групп антисимметрии: ) может быть "зацвечена" или стать классической подгруппой. Отсюда имеем три варианта групп антисимметрии:
m . 2' = m .  = =  , 2 . m' = 2 . , 2 . m' = 2 .  = = 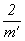 , , 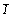 . m' = . m' = 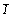 . 2' = . 2' =  . Однако поскольку все члены этой группы представлены разными элементами симметрии, то, несмотря на их взаимосвязь, следует рассмотреть все три варианта "зацвечивания" элементов симметрии. . Однако поскольку все члены этой группы представлены разными элементами симметрии, то, несмотря на их взаимосвязь, следует рассмотреть все три варианта "зацвечивания" элементов симметрии.
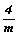 - подгруппа 8-го порядка (41, 42 = 2, 43 = 4-1, 44 = 1, - подгруппа 8-го порядка (41, 42 = 2, 43 = 4-1, 44 = 1, 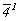 , , 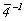 , m, , m, 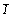 ) (рис. 140). Выписав подгруппы 4-го порядка: 4(1, 41, 42 = 2, 43), ) (рис. 140). Выписав подгруппы 4-го порядка: 4(1, 41, 42 = 2, 43), 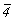 (1, (1, 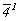 , , 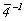 , 2), , 2), 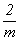 (1, (1, 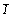 , m, 2) - и добавив к ним удваивающие антиоперации (m', , m, 2) - и добавив к ним удваивающие антиоперации (m', 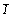 , 4'(mod2) или , 4'(mod2) или 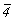 (mod2)), получим 3 группы антисимметрии: (mod2)), получим 3 группы антисимметрии:

Путем поочередного "зацвечивания" порождающих элементов симметрии получим те же три группы антисимметрии: 
 - группа 16-го порядка. Взаимодействие подгрупп 8-го порядка - 422, 4mm, - группа 16-го порядка. Взаимодействие подгрупп 8-го порядка - 422, 4mm, 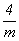 , , 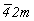 , mmm(!) - c удваивающими операциями антисимметрии приведет к следующим пяти группам симметрии (см. цветную вставку, рис. 141): , mmm(!) - c удваивающими операциями антисимметрии приведет к следующим пяти группам симметрии (см. цветную вставку, рис. 141):
422 ? m'z (m'x, m'd) = 
(взаимодействие осевого комплекса 422 с антиплоскостью m' любой позиции символа приведет к появлению цветного центра симметрии  , а следовательно, и остальных элементов антисимметрии тетрагональной голоэдрии; если удваивающей операцией считать антиинверсию , а следовательно, и остальных элементов антисимметрии тетрагональной голоэдрии; если удваивающей операцией считать антиинверсию  , то придем к тому же результату); не следует забывать и удваивающие операции антисимметрии , то придем к тому же результату); не следует забывать и удваивающие операции антисимметрии  ; ;
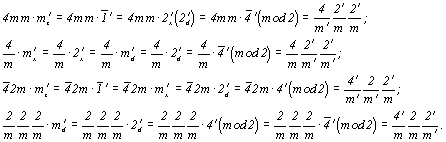
Приняв за порождающие элементы плоскости симметрии трех разных позиций символа, рассмотрим все различные варианты их "зацвечивания" (рис. 141). "Зацветив" только плоскость 1-й позиции - горизонтальную плоскость, получим координатные и диагональные оси антисимметрии 2' : 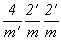 . Если же элементом антисимметрии считать одну из плоскостей 2-й или 3-й позиции символа, то возникнут одинаковые группы антисимметрии, различающиеся лишь установкой (поменяются координатные и диагональные направления): . Если же элементом антисимметрии считать одну из плоскостей 2-й или 3-й позиции символа, то возникнут одинаковые группы антисимметрии, различающиеся лишь установкой (поменяются координатные и диагональные направления):  = = 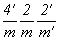 . .
<ЩЗацвечивание> двух иcходных плоскостей симметрии (горизонтальной и одной из вертикальных или только плоскостей 2-й и 3-й позиций одновременно) приведет к двум группам антисимметрии: 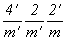 = = 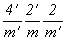 и и 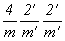 . И наконец, "цветные" плоскости всех трех позиций дадут группу . И наконец, "цветные" плоскости всех трех позиций дадут группу 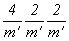 . .
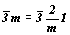 - группа 12-го порядка. Подгруппы 6-го порядка: - группа 12-го порядка. Подгруппы 6-го порядка:  , 32, 3m, взаимодействуя с элементами антисимметрии 2-го порядка ( , 32, 3m, взаимодействуя с элементами антисимметрии 2-го порядка (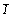 ' , m', 2'), дадут три группы антисимметрии: ' , m', 2'), дадут три группы антисимметрии:
3m . 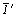 = 3m . 2' = = 3m . 2' = 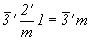
(обратим внимание на то, что поскольку ось 3 не может быть элементом антисимметрии (см. рис. 137), штрих относится лишь к центру инверсии);
32 . 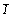 = 32. m' = = 32. m' = 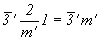 ; ;
 . m' = . m' =  . 2' = . 2' = 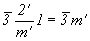 . .
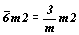 - группа 12-го порядка. Подгруппы 6-го порядка: 32, 3m, - группа 12-го порядка. Подгруппы 6-го порядка: 32, 3m, 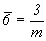 . Удваивающие антиоперации: m', 2'. Изоморфные группы антисимметрии (см. цветную вставку, рис. 142) 1): . Удваивающие антиоперации: m', 2'. Изоморфные группы антисимметрии (см. цветную вставку, рис. 142) 1):
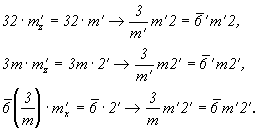
23 - группа 12-го порядка. Не имеет подгрупп порядка 6, поэтому изоморфных ей групп антисимметрии нет. Кажущееся возможным "зацвечивание" осей 2-го порядка приведет лишь к серой группе 23. 1'.
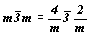 - группа 48-го порядка. Подгруппы 24-го порядка: 432, - группа 48-го порядка. Подгруппы 24-го порядка: 432, 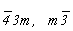 . Удваивающие антиоперации: . Удваивающие антиоперации: 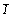 ', 2', m', 4' (mod2), ', 2', m', 4' (mod2), 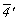 (mod2). Группы антисимметрии (см. цветную вставку, рис. 143): (mod2). Группы антисимметрии (см. цветную вставку, рис. 143):
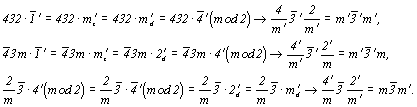
Итак, используя рассмотренные пути вывода шубниковских точечных групп симметрии, можно на основе 32 классических полярных групп (введением операции антитождества 1' ) получить 32 нейтральные (серые) группы и 58 групп смешанной полярности - собственно групп антисимметрии, т.е. всего 122 группы (табл. 5), с помощью которых можно описать симметрию конечных фигур и объектов, обладающих какими-либо прямо противоположными негеометрическими свойствами (рис. 144). В частности, группы антисимметрии используются в кристаллографической практике при выводе законов двойникования, описания симметрии двойников, электрических, магнитных (см. с. 20) и других свойств кристаллов.
Геологический факультет МГУ
|


