|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.11. Вывод пространственных групп гексагональной сингонии
Классный метод вывода пространственных групп гексагональной сингонии, предложенный Н.В.Беловым [5, 18] (см. с. 217), предполагает рассмотрение возможности задания на различных позициях гексагонального символа плоскостей или осей симметрии в качестве порождающих элементов симметрии. Однако такой вывод не показывает связи гексагональных групп с группами других, выше выведенных сингоний, т.е. неоправданно обособляет их. С этой точки зрения интересно проследить взаимосвязь групп гексагональной сингонии с одной главной осью 3-го порядка, самостоятельной или являющейся составной частью оси более высокого порядка - 6, с кубическими пространственными группами, содержащими несколько осей 3-го порядка [26]. Такую связь нетрудно увидеть уже на уровне элементарных ячеек, сориентировав куб вдоль одной из осей 3-го порядка. Очевидно, что незначительная деформация гексаэдра - частного случая ромбоэдра с углами  = =  = =  = 90o - вдоль этой оси ликвидирует все наклонные к оси 3 элементы симметрии, не свойственные ромбоэдру. Сам же ромбоэдр в этом случае, хотя его и можно рассматривать в качестве примитивного параллелепипеда (a = b = c, = 90o - вдоль этой оси ликвидирует все наклонные к оси 3 элементы симметрии, не свойственные ромбоэдру. Сам же ромбоэдр в этом случае, хотя его и можно рассматривать в качестве примитивного параллелепипеда (a = b = c,  = =  = =   90o ), не будет ячейкой Браве, ибо его ребра не связаны с особыми направлениями. Это делает необходимым выбор новой гексагональной элементарной ячейки. 90o ), не будет ячейкой Браве, ибо его ребра не связаны с особыми направлениями. Это делает необходимым выбор новой гексагональной элементарной ячейки.
Трансформацию симметрии кубической ячейки в гексагональную легко проиллюстрировать на уровне точечных групп симметрии (рис. 117, б, в), в результате которой каждая из пяти групп кубической сингонии переходит в соответствующую ей тригональную группу. При этом в тригональных группах останется лишь половина диагональных, перпендикулярных оси 3-го порядка особых направлений кубических групп.
Остальные - собственно гексагональные - точечные группы легко вывести, воспользовавшись удачно предложенным Н.В.Беловым механизмом [5, 18]: добавлением к оси 3 (главному особому направлению тригональных групп) совпадающей с ней оси 2-го порядка - простой (2) или инверсионной (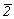 = m): = m):
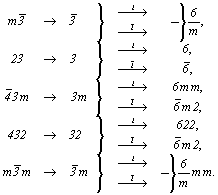
Сначала следует рассмотреть вопрос о направлении координатных трансляционных векторов стандартных дважды центрированных R-ячеек Браве, выбранных в кубических решетках каждого типа (Р, I или F).
В качестве координатных векторов  и и  новой гексагональ-ной ячейки выбираются бывшие диагонали граней исходного Р-куба, став-шие в новой ячейке горизонтальными трансляциями с углом между ними, равным 120o (рис. 118, а). Расположение же всех узлов кубической Р-ячейки, ориентированной вдоль одной из осей 3-го порядка, на трех уровнях (0, 1/3, 2/3) относительно телесной диагонали куба - ее нового гексагонального параметра новой гексагональ-ной ячейки выбираются бывшие диагонали граней исходного Р-куба, став-шие в новой ячейке горизонтальными трансляциями с углом между ними, равным 120o (рис. 118, а). Расположение же всех узлов кубической Р-ячейки, ориентированной вдоль одной из осей 3-го порядка, на трех уровнях (0, 1/3, 2/3) относительно телесной диагонали куба - ее нового гексагонального параметра 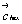 - указывает на дважды объемноцентрированный тип (R) решетки Браве (рис. 118, а). В векторном выражении - указывает на дважды объемноцентрированный тип (R) решетки Браве (рис. 118, а). В векторном выражении
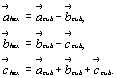
Если исходной является кубическая объемноцентрированная ячейка, то дополнительный вектор 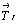 , ставший в гексагональной установке вертикальным, сокращает вдвое параметр , ставший в гексагональной установке вертикальным, сокращает вдвое параметр 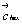 по сравнению с таковым производной от кубической Р-ячейки (рис. 118, б). Горизонтальные же параметры по сравнению с таковым производной от кубической Р-ячейки (рис. 118, б). Горизонтальные же параметры 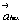 и и 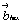 по абсолютной величине остаются прежними. Однако для сохранения единообразия центрировки гексагональной ячейки можно выбрать следующие координатные направления : по абсолютной величине остаются прежними. Однако для сохранения единообразия центрировки гексагональной ячейки можно выбрать следующие координатные направления :
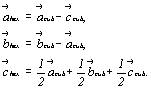
В F-решетке из множества дополнительных трансляций, центрирующих грани куба, можно выбрать две горизонтальные, расположенные под углом 120o одна к другой, каждая из которых равна половине диагонали грани кубической ячейки. При этом вертикальный параметр ячейки 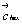 остается равным телесной диагонали исходного куба (ромбоэдра) (рис. 118, в). Для такой новой R-ячейки Браве остается равным телесной диагонали исходного куба (ромбоэдра) (рис. 118, в). Для такой новой R-ячейки Браве
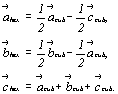
В итоге убеждаемся, что каждому типу кубических решеток Браве соответствует определенная гексагональная дважды центрированная ячейка с определенной ориентацией и размерами координатных векторов 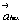 , , 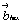 , , 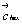 . Далее, зная взаимосвязь кубических ячеек разного типа (Р, I, F) с соответствующими им гексагональными R-ячейками, можно вывести пространственные группы гексагональной сингонии на основе кубических пространственных групп. . Далее, зная взаимосвязь кубических ячеек разного типа (Р, I, F) с соответствующими им гексагональными R-ячейками, можно вывести пространственные группы гексагональной сингонии на основе кубических пространственных групп.
Вывод пространственных групп тригональной подсингонии с R-решеткой на основе кубических пространственных групп
Прежде чем приступить к выводу гексагональных пространственных групп симметрии, полезно вспомнить прослеженную ранее связь (см. с. 162) кубических групп с группами ромбической и тетрагональной сингоний, которую легко представить на уровне точечных групп (см. рис. 117). Кубизация двух ромбических групп (222 и mmm) и трех тетрагональных (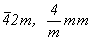 ) путем введения равнонаклонной к координатным направлениям оси 3[111] приводит к пяти точечным группам кубической сингонии (см. рис. 117, а, б), последующая гексагонализация которых вышеуказанным способом приведет также к пяти точечным группам тригональной подсингонии (см. рис. 117, в). Подмеченную связь попытаемся проследить и на уровне пространственных групп. ) путем введения равнонаклонной к координатным направлениям оси 3[111] приводит к пяти точечным группам кубической сингонии (см. рис. 117, а, б), последующая гексагонализация которых вышеуказанным способом приведет также к пяти точечным группам тригональной подсингонии (см. рис. 117, в). Подмеченную связь попытаемся проследить и на уровне пространственных групп.
Для кубизации годятся лишь те пространственные группы, в которых на всех трех позициях символа расположены одинаковые (однотипные) элементы симметрии, ибо только в этом случае введение кубизирующей оси 3-го порядка сделает их эквивалентными. Из всех пяти подлежащих кубизации групп кубической осевой гемиэдрии, выведенных на основе пространственных групп, подчиненных точечным 222 и mmm (см. с. 107, 119), получим единственную пространственную группу с ромбоэдрической решеткой - R3, в которую перейдет лишь одна ось 3-го порядка каждой из них, координатные же оси 2 и 21 окажутся несовместимы с R-решеткой:
| Пр. группы ромбической осевой гемиэдрии |
Пр. группы кубической осевой тетартоэдрии |
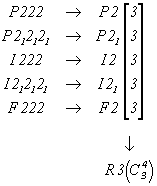 |
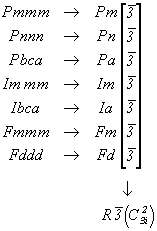
Каждая из семи групп кубической гемиэдрии трансформируется при гексагонализации в одну и ту же ромбоэдрическую - 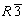 : :
| Пр. группы ромбической голоэдрии |
Пр. группы кубической голоэдрии |
 |
Гексагонализация пространственных групп кубической осевой гемиэдрии, выведенных на основе тетрагональных групп класса 422, приведет также к одной ромбоэдрической группе: R32. При этом для получения кубических пространственных групп с F-решеткой следует соответствующие I-группы представить в F-аспекте:
| Пр. группы тетрагональ- ной осевой гемиэдрии |
Пр. группы кубической осевой гемиэдрии |
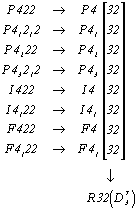 |
В списке кубических пространственных групп, подчиненных точечной 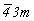 , можно выделить те из них, на 3-й позиции символов которых располагаются зеркальные плоскости симметрии. Гексагонализация этих групп даст одну группу - R3m 1 : , можно выделить те из них, на 3-й позиции символов которых располагаются зеркальные плоскости симметрии. Гексагонализация этих групп даст одну группу - R3m 1 :
| Пр. группы тетрагональной гемиэдрии |
Пр. группы кубической гемиэдрии |
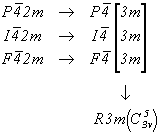 |
Гексагонализация перечисленных выше кубических групп не вызывает затруднений, так как зеркальные плоскости при таком переходе не меняют свое наименование. Во втором семействе кубических групп: 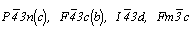 и и 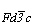 - на третьей позиции их символов оказываются плоскости, меняющие в новой ориентировке свои обозначения. В группах - на третьей позиции их символов оказываются плоскости, меняющие в новой ориентировке свои обозначения. В группах 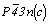 и и 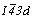 косые векторы скольжения диагональных клиноплоскостей n и d кубической ячейки в ячейке ромбоэдрической оказываются вертикальными, т.е. параллельными косые векторы скольжения диагональных клиноплоскостей n и d кубической ячейки в ячейке ромбоэдрической оказываются вертикальными, т.е. параллельными 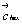 . При этом в гексагональных группах, производных от Р- и F-кубических ячеек (рис. 119, а, б), клиноплоскость n просто меняет свое наименование на с, т.е. . При этом в гексагональных группах, производных от Р- и F-кубических ячеек (рис. 119, а, б), клиноплоскость n просто меняет свое наименование на с, т.е. 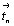 превращается в превращается в 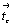 . При переходе к гексагональной ячейке от I-кубической трансляционный вектор . При переходе к гексагональной ячейке от I-кубической трансляционный вектор 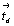 клиноплоскости d, равный 1/4 телесной диагонали исходного куба (рис. 119, в), в новой ромбоэдрической ячейке с вдвое сокращенным параметром клиноплоскости d, равный 1/4 телесной диагонали исходного куба (рис. 119, в), в новой ромбоэдрической ячейке с вдвое сокращенным параметром 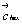 по сравнению с аналогичными параметрами производных от Р- и F-кубических ячеек также превращается в трансляционную компоненту плоскости с ( по сравнению с аналогичными параметрами производных от Р- и F-кубических ячеек также превращается в трансляционную компоненту плоскости с (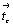 ), т.е. и в этом случае клиноплоскость d превращается в плоскость с. ), т.е. и в этом случае клиноплоскость d превращается в плоскость с.
Особого внимания заслуживает трансформация кубических пространственных F-групп с плоскостями с на третьей позиции символа - гемиэдрической 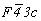 и голоэдрических и голоэдрических 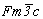 и и 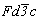 . Указанные пространственные группы получены в качестве надгрупп тетрагональных: . Указанные пространственные группы получены в качестве надгрупп тетрагональных: 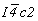 , , 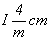 и и 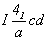 соответственно, представленных в пригодном для кубизации F-аспекте: соответственно, представленных в пригодном для кубизации F-аспекте: 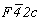 , , 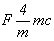 и и 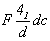 (см. с. 166), в котором координатная трансляция (см. с. 166), в котором координатная трансляция 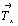 ( (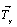 ) I-решетки, становясь дополнительным центрирующим грань ячейки вектором, совпадает с теперь уже диагональной плоскостью с (рис. 120). Взаимодействие плоскости сd с лежащим в ней вектором ) I-решетки, становясь дополнительным центрирующим грань ячейки вектором, совпадает с теперь уже диагональной плоскостью с (рис. 120). Взаимодействие плоскости сd с лежащим в ней вектором 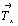 (cd . (cd . 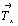 = md . = md . 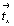 . . 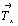 ) превратит ее в клиноплоскость n, т.е. будет наблюдаться тождественность плоскостей с и n (c ) превратит ее в клиноплоскость n, т.е. будет наблюдаться тождественность плоскостей с и n (c  n). В развернутом виде группа запишется n). В развернутом виде группа запишется 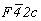  n. Клиноплоскость n, как было показано выше, в ромбоэдрической установке "работает" как плоскость с. Таким образом, гексагонализация трех из перечисленных выше кубических пространственных групп приведет к одной ромбоэдрической - R3c: n. Клиноплоскость n, как было показано выше, в ромбоэдрической установке "работает" как плоскость с. Таким образом, гексагонализация трех из перечисленных выше кубических пространственных групп приведет к одной ромбоэдрической - R3c:
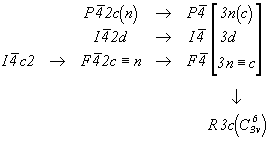
Указанную особенность диагональных плоскостей с (с  n) следует учитывать и при гексагонализации голоэдрических групп кубической сингонии, каждая из которых имеет своей подгруппой соответствующую тетрагональную группу: n) следует учитывать и при гексагонализации голоэдрических групп кубической сингонии, каждая из которых имеет своей подгруппой соответствующую тетрагональную группу:
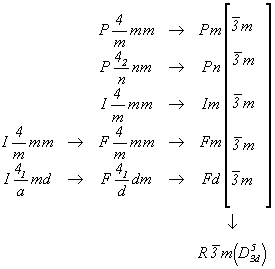
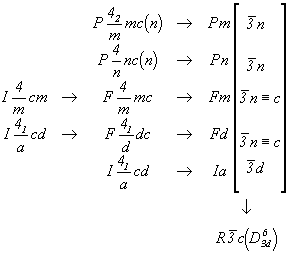
В символах пространственных групп R3c и 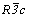 сохраняется обозначение плоскости скользящего отражения с. Исходная же плоскость c кубической группы преобразуется в своеобразную клиноплоскость r [29, 30] с необычными для клиноплоскости трансляционными компонентами (см. с. 226 - 229). сохраняется обозначение плоскости скользящего отражения с. Исходная же плоскость c кубической группы преобразуется в своеобразную клиноплоскость r [29, 30] с необычными для клиноплоскости трансляционными компонентами (см. с. 226 - 229).
В итоге, воспользовавшись приемом гексагонализации кубических пространственных групп получили все ромбоэдрические группы гексагональной сингонии (табл. 3).
Вывод пространственных групп тригональной подсингонии с Р-решеткой
Приведенная выше табл. 3 помимо перехода от кубических групп к ромбоэдрическим демонстрирует и переход от семи групп с ромбоэдрической решеткой к остальным пространственным группам тригональной подсингонии с Р-решеткой Браве, который легко осуществляется снятием R-трансляций. При этом следует помнить, что в R-решетке все три сорта осей 3-го порядка (3, 31 и 32) взаимосвязаны, ибо взаимодействие одной из них (например, оси 3, расположенной в начале координат) с двумя дополнительными трансляционными векторами R-ячейки
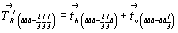 и и 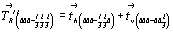
приведет к появлению порожденных осей 3-го порядка иного характера - 31 и 32 - в позициях 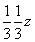 и и 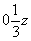 соответственно (см. рис. 99). При переходе к Р-ячейке эти оси становятся независимыми, что увеличивает количество соответствующих Р-групп. Кроме того, особые направления 2, соответственно (см. рис. 99). При переходе к Р-ячейке эти оси становятся независимыми, что увеличивает количество соответствующих Р-групп. Кроме того, особые направления 2, 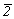 = m и 21 , запрещенные в R-ячейке на третьей - апофемальной - позиции символа, примитивной ячейке не противоречат. Это удваивает количество соответствующих Р-групп. Центросимметричные Р-группы не могут содержать винтовые оси 31 и 32, ибо взаимодействие их с центром инверсии привело бы к абсурдному расположению узлов элементарной ячейки. В итоге получим 18 пространственных групп тригональной подсингонии с примитивной решеткой Браве (см. таблицу 3). = m и 21 , запрещенные в R-ячейке на третьей - апофемальной - позиции символа, примитивной ячейке не противоречат. Это удваивает количество соответствующих Р-групп. Центросимметричные Р-группы не могут содержать винтовые оси 31 и 32, ибо взаимодействие их с центром инверсии привело бы к абсурдному расположению узлов элементарной ячейки. В итоге получим 18 пространственных групп тригональной подсингонии с примитивной решеткой Браве (см. таблицу 3).
Вывод собственно гексагональных пространственных групп
Переход от групп тригональной подсингонии (с главной осью 3-го порядка) к пространственным группам собственно гексагональной сингонии (с главной осью 6-го порядка) может быть осуществлен путем совмещения оси 3 - главного особого направления - с осями 2, 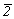 или 21 , что повысит ее порядок до шести. Такой переход уже был продемонстрирован на примере точечных групп симметрии (см. с. 207). В результате из пяти тригональных точечных групп были получены 7 собственно гексагональных. или 21 , что повысит ее порядок до шести. Такой переход уже был продемонстрирован на примере точечных групп симметрии (см. с. 207). В результате из пяти тригональных точечных групп были получены 7 собственно гексагональных.
Однако вывод собственно гексагональных пространственных групп на основе ромбоэдрических указанным способом невозможен, ибо возникающие в этом случае оси 6-го порядка несовместимы с R-решеткой. Таким образом, гексагонализации подлежат лишь 18 пространственных групп тригональной подсингонии с Р-решеткой (таблица 4). При выводе следует учесть целесообразность добавления различных осей 2-го порядка (2, 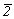 или 21) к тем или иным примитивным группам тригональной подсингонии [18]. или 21) к тем или иным примитивным группам тригональной подсингонии [18].
Действительно, если оси 2 и 21 могут взаимодействовать со всеми осями 3-го порядка (3, 31 , 32) , то ось 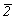 = mz можно добавлять к группам, содержащим лишь поворотные оси 3, в результате чего возникнет ось = mz можно добавлять к группам, содержащим лишь поворотные оси 3, в результате чего возникнет ось 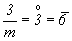 . Следует также иметь в виду, что в центросимметричных группах оси 2 и . Следует также иметь в виду, что в центросимметричных группах оси 2 и 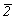 неизбежно сопровождают одна другую, так как введение одной из них приводит к автоматическому появлению другой. неизбежно сопровождают одна другую, так как введение одной из них приводит к автоматическому появлению другой.
Из таблицы 4 видно, что исходные пространственные группы тригональной подсингонии, содержащие боковые (горизонтальные) особые направления на разных позициях символа, объединяются в пары, ибо повышение порядка главной оси до шести делает особые направления обеих (2-й и 3-й) позиций взаимосвязанными.
Предложенный вывод пространственных групп гексагональной сингонии на основе кубических демонстрирует их тесную связь, продолжая намеченную ранее цепочку вывода: от ромбических --> через тетрагональные --> к кубическим и далее к гексагональным, ликвидируя таким образом обособленность последних, особенно остро ощущаемую при "классном" их выводе, когда простой перебор порождающих элементов симметрии на соответствующих позициях символа оказывается хотя и полезным, но недостаточно продуктивным при выявлении симметрийной связи пространственных групп разных сингоний.
Геологический факультет МГУ
|


