|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.10. Графическое представление пространственных групп кубической сингонии
Условные обозначения элементов симметрии
Приступая к построению графиков пространственных групп кубической сингонии, необходимо прежде всего дополнить "инвентарь" условных обозначений элементов симметрии, используемых в графиках пространственных групп низшей и средней категорий.
Действительно, хотя в кубических пространственных группах встречаются все те же оси симметрии кристаллографических порядков (поворотные, винтовые, инверсионные = зеркальные), плоскости симметрии (зеркальные и скользящего отражения), однако ориентация многих из них в группах высшей категории специфична, что и отражено в их обозначениях на графиках пространственных групп. Для того чтобы по возможности исключить формальное заучивание или "рабскую" прикованность к таблицам, остановимся подробнее на таких, главным образом нетривиальных, обозначениях [16, 17].
Из уже рассмотренных графиков пространственных групп низшей и средней категорий в кубическую сингонию без изменений переходят обозначения вертикальных (т.е. перпендикулярных плоскости чертежа) поворотных и винтовых осей симметрии любых кристаллографических порядков. Обозначения горизонтальных осей 2-го порядка не претерпевают изменений: "стрелки" вынесены на поля графика за пределы обозначенной элементарной ячейки с указанием их высоты (уровня) над плоскостью чертежа в долях параметра с (рис. 94).
Принципиальная "новость" - горизонтальные оси 4-го порядка (отсутствующие в низшей и средней категориях). Их обозначения так же, как и обозначения осей 2-го порядка, выносятся на поля графика за пределы ячейки и имеют вид деформированных квадратов - параллелограммов, "нанизанных" на оси. При этом длинная сторона каждого параллелограмма перпендикулярна направлению оси (рис. 94, а).
Инверсионные оси 4-го порядка фиксируются на графиках лишь своими особыми точками, но вместо маловыразительной "точки" изображают "зеркало" (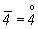 ! ) - пустой незачерненный квадрат ( ! ) - пустой незачерненный квадрат ( ) - для вертикальных осей или параллелограмм, нанизанный на горизонтальную ось ) - для вертикальных осей или параллелограмм, нанизанный на горизонтальную ось 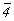 ( (  ), с указанием высоты ее особых точек (а следовательно, высоты самой оси, если она горизонтальна) в долях параметра с элементарной ячейки (рис. 94, б). ), с указанием высоты ее особых точек (а следовательно, высоты самой оси, если она горизонтальна) в долях параметра с элементарной ячейки (рис. 94, б).
Для обозначения характерных лишь для кубических групп наклонных элементов симметрии - осей 2-го и 3-го порядков (параллельных соответственно гранным и телесным диагоналям кубической ячейки) - используются незачерненные фюзо и треугольники, пронзенные векторами (осями, порядок которых они символизируют). Нижние концы таких наклонных осей, отмеченные точками, указывают место их выхода с нулевого уровня вверх (рис. 94, в, г).Координатные плоскости симметрии - вертикальные и горизонтальная - обозначаются так же, как и на графиках пространственных групп низшей и средней категорий. Однако диагональные вертикальные плоскости неизменно сопровождаются связанными с ними наклонными диагональными плоскостями, попарно образующими как бы двускатную крышу. На графиках показывают "конек" такой крыши, находящийся на нулевом вдоль оси Z уровне, и ее скаты. Стрелки на скатах указывают направление трансляционных компонент пересекающихся наклонных плоскостей скользящего отражения (рис. 94, д).
В кристаллографической литературе можно встретить некоторые устаревшие либо современные, но малоудачные, на наш взгляд, обозначения элементов симметрии пространственных групп кубической сингонии [17, 73]. Поэтому считаем полезным вкратце остановиться на них.
1. Наклонные оси 2-го порядка изображались в виде по-разному ориентированных тригональных (!) призм, из граней которых выходят стрелки (оси), направленные с нулевого уровня вверх:
 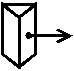 . .
2. Пересечение с осью 3-го порядка всех трех координатных инверсионных осей 4-го порядка, а следовательно, всех элементов симметрии комплекса 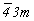 , обозначались квадратом, перечеркнутым одной диагональю: , обозначались квадратом, перечеркнутым одной диагональю:  . .
3. Для изображения наклонных плоскостей симметрии в последнем издании Интернациональных таблиц [73] используется стереограмма всех (и трансляционных тоже) элементов симметрии, пересекающихся в определенных точках (рис. 95).
Все только что перечисленные обозначения элементов симметрии и их комплексов, на наш взгляд, неудачны, так как выпадают из общей идеи, заложенной в условные обозначения элементов симметрии пространственных групп различных категорий, и излишне загромождают их графики. Поэтому авторы "Атласа пространственных групп кубической системы" [16], отказавшись от подобных условных знаков, постарались использовать обозначения, во многом повторяющие первоначальную символику первого автора графиков пространственных групп Е.С.Федорова (см. [17]).
Пространственная группа 
Построение графика пространственной группы 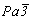 удобно начать с вычерчивания ее исходной ромбической подгруппы Рbca с одинаковыми параметрами элементарной ячейки, кубизация которой введением оси 3-го порядка делает все координатные особые направления эквивалентными. удобно начать с вычерчивания ее исходной ромбической подгруппы Рbca с одинаковыми параметрами элементарной ячейки, кубизация которой введением оси 3-го порядка делает все координатные особые направления эквивалентными.
Посчитав плоскости b, c, a всех трех позиций ромбического символа порождающими элементами симметрии, в качестве результата их взаимодействий получим винтовые оси 2-го порядка и центр инверсии (рис. 96, а). Для ввода оси 3-го порядка наиболее приемлемой является нонвариантная позиция (см. с. 184) в центре инверсии, равноудаленная в пр. гр. Рbca от всех трех скрещивающихся координатных осей 21 и трех плоскостей симметрии (рис. 96, б). Действительно, задание оси 3[111] в указанную позицию, принятую за начало координат (с соответствующим изменением высот элементов симметрии), не размножает (а переводит в себя) ни осевой, ни плоскостной комплекс исходной ромбической группы. Поэтому процесс вычерчивания графика искомой пр. гр. 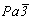 сводится к размножению заданной материализованной оси 3-го порядка либо всеми плоскостями симметрии, либо осями симметрии 2-го порядка пространственной группы с последующей фиксацией найденных осей 3 на нулевом (относительно оси Z) уровне. Поскольку и плоскости симметрии b, c, a, и винтовые оси 21 содержат трансляционные компоненты, направленные вдоль всех трех координатных осей X, Y и Z, то оси 3-го порядка, размноженные ими, как бы "разбегутся" вдоль указанных векторов. сводится к размножению заданной материализованной оси 3-го порядка либо всеми плоскостями симметрии, либо осями симметрии 2-го порядка пространственной группы с последующей фиксацией найденных осей 3 на нулевом (относительно оси Z) уровне. Поскольку и плоскости симметрии b, c, a, и винтовые оси 21 содержат трансляционные компоненты, направленные вдоль всех трех координатных осей X, Y и Z, то оси 3-го порядка, размноженные ими, как бы "разбегутся" вдоль указанных векторов.
Рассмотрим последовательные действия на исходную ось 3[111] каждой из указанных трансляционных плоскостей симметрии (рис. 97), при этом дробью (1/2) отметим оси 3-го порядка, точки входа которых расположены на полтрансляции вдоль оси Z. Отраженная в плоскости bx = mx. 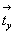 ось 3[111] , получив символ 3 ось 3[111] , получив символ 3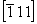 , сначала займет положение 2 и затем будет перенесена трансляционной компонентой этой плоскости в положение 3 без изменения своей высоты по оси Z (рис. 97, а). Та же ось 3[111] под действием плоскости сy = my . , сначала займет положение 2 и затем будет перенесена трансляционной компонентой этой плоскости в положение 3 без изменения своей высоты по оси Z (рис. 97, а). Та же ось 3[111] под действием плоскости сy = my . 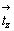 (рис. 97, б), отразившись в ней, получит символ 3 (рис. 97, б), отразившись в ней, получит символ 3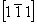 и, перемещенная вдоль оси Z на и, перемещенная вдоль оси Z на  , будет зарегистрирована на нулевом уровне в позиции 3, а затем трансляцией решетки , будет зарегистрирована на нулевом уровне в позиции 3, а затем трансляцией решетки 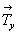 внесена в элементарную ячейку в положение 4. Горизонтальной плоскостью az = mz . внесена в элементарную ячейку в положение 4. Горизонтальной плоскостью az = mz . 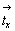 , расположенной на высоте , расположенной на высоте 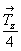 , ось 3[111] будет переведена с нулевого уровня в положение 2 (3 , ось 3[111] будет переведена с нулевого уровня в положение 2 (3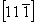 ) и затем в положение 3 на высоте ) и затем в положение 3 на высоте  ; на нулевом уровне она окажется в положении 4 (рис. 97, в). ; на нулевом уровне она окажется в положении 4 (рис. 97, в).
В случае отсутствия плоскостей симметрии, например в пространственной группе герсдорфита NiAsS - Р213 (подгруппа группы 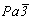 ), размножающим будет комплекс скрещивающихся осей 21. А так как этот комплекс осей является производным от взаимодействия плоскостей симметрии b, c, a, то в итоге получим то же самое расположение осей 3-го порядка: ), размножающим будет комплекс скрещивающихся осей 21. А так как этот комплекс осей является производным от взаимодействия плоскостей симметрии b, c, a, то в итоге получим то же самое расположение осей 3-го порядка:
- ось 21(x) (рис. 97, г) повернет исходную ось 3[111] на 180o в положение 2 (3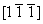 ) и сместит на полтрансляции вдоль оси X в положение 3; выход этой оси с нулевого уровня вверх будет иметь символ [ ) и сместит на полтрансляции вдоль оси X в положение 3; выход этой оси с нулевого уровня вверх будет иметь символ [ ] (положение 4); ] (положение 4);
- ось 21(y) (рис. 97, д), расположенная на высоте 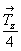 , повернет исходную ось 3[111] в положение 2 (3 , повернет исходную ось 3[111] в положение 2 (3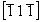 ) на высоте 1/2 по оси Z и далее перенесет в положение 3, окончательная позиция этой оси (3 ) на высоте 1/2 по оси Z и далее перенесет в положение 3, окончательная позиция этой оси (3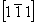 ) на нулевом уровне будет в положении 4; ) на нулевом уровне будет в положении 4;
- поворот и скольжение вокруг оси 21(z) (рис. 97, в) переведут исходную ось 3[111] в положение 2 (3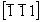 ) на высоту ) на высоту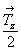 , и нулевой ее выход (положение 3) окажется за рамками выделенной элементарной ячейки; внесенная в ячейку ось 3 , и нулевой ее выход (положение 3) окажется за рамками выделенной элементарной ячейки; внесенная в ячейку ось 3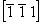 будет локализована в положении 4. будет локализована в положении 4.
Таким образом, в результате проведенных операций симметрии получим 4 выхода поворотных осей 3-го порядка (см. рис. 96, в).
График пространственной группы 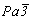 будет завершен (см. рис. 96, г), если на него нанести винтовые оси 31 и 32, всегда сопровождающие в кубических пространственных группах поворотные оси 3-го порядка и возникающие как результат их взаимодействия с группами трансляций каждой из трех кубических решеток Браве. будет завершен (см. рис. 96, г), если на него нанести винтовые оси 31 и 32, всегда сопровождающие в кубических пространственных группах поворотные оси 3-го порядка и возникающие как результат их взаимодействия с группами трансляций каждой из трех кубических решеток Браве.
Для определения взаимного расположения осей 3-го порядка (3, 31, 32) удобно, сориентировав кубическую элементарную ячейку вдоль одной из осей 3-го порядка, представить ее в гексагональном аспекте как частный случай R-решетки.
И поскольку в каждой из кубических решеток (Р, I или F) можно выделить основную ячейку в виде примитивного ромбоэдра (рис. 98), а следовательно, дважды центри-рованную гексагональную ячейку Браве, то, рассмотрев взаимодействие главной оси такой ячейки (оси 3) с ее дополнительными трансляци-онными векторами 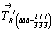 и и 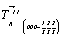 (рис. 99), можно определить характер и положение результирующих осей 31 и 32 . (рис. 99), можно определить характер и положение результирующих осей 31 и 32 .
Вертикальные составляющие 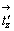 и и 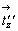 векторов векторов 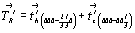 и и 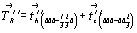 , добавленные к операции поворота на 120o вокруг оси 3, превратят ее в винтовые 31 и 32 соответственно. Горизонтальные же составляющие , добавленные к операции поворота на 120o вокруг оси 3, превратят ее в винтовые 31 и 32 соответственно. Горизонтальные же составляющие 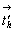 и и 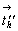 этих векторов перенесут возникшие винтовые оси в центры построенных на них треугольников (см. с. 54) в сторону вращения результирующих осей, характер и положение которых подтверждаются и высотами узлов дважды центрированной R-ячейки (рис. 99). этих векторов перенесут возникшие винтовые оси в центры построенных на них треугольников (см. с. 54) в сторону вращения результирующих осей, характер и положение которых подтверждаются и высотами узлов дважды центрированной R-ячейки (рис. 99).
Далее, рассмотрев положения полученных винтовых осей 31 и 32 на гранях исходного ромбоэдра (Р-куба) (рис. 100, а), увидим, что эти оси параллельны главной исходной оси 3 ромбоэдра и пересекают его грани (например, грань АВСD) в точках, делящих их горизонтальные диагонали (BD) на три равные части. Размножив полученные таким образом оси 31 и 32, определим их положения и на соседних гранях основного ромбоэдра (куба).
В кубической I-ячейке за счет присутствия центрирующего объем вектора 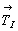 , равного половине телесной диагонали исходного куба, вдвое сокращается трансляция вдоль оси 3-го порядка выделенной основной ячейки (ромбоэдра), а следовательно, и вертикальный параметр с соответствующей гексагональной дважды центрированной R-ячейки Браве. Соответственно сокращаются вдвое и вертикальные составляющие , равного половине телесной диагонали исходного куба, вдвое сокращается трансляция вдоль оси 3-го порядка выделенной основной ячейки (ромбоэдра), а следовательно, и вертикальный параметр с соответствующей гексагональной дважды центрированной R-ячейки Браве. Соответственно сокращаются вдвое и вертикальные составляющие 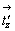 и и 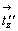 векторов векторов 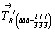 и и 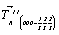 (рис. 100, б). Это приводит к тому, что ось 31 оказывается в позиции 32 кубической Р-ячейки (и соответственно ось 32 совпадает с осью 31), т.е. на грани (001) исходного I-куба положение энантиоморфных осей 31 и 32 по сравнению с их положением на этой же грани в Р-ячейке меняются местами (рис. 100, б). (рис. 100, б). Это приводит к тому, что ось 31 оказывается в позиции 32 кубической Р-ячейки (и соответственно ось 32 совпадает с осью 31), т.е. на грани (001) исходного I-куба положение энантиоморфных осей 31 и 32 по сравнению с их положением на этой же грани в Р-ячейке меняются местами (рис. 100, б).
В кубической F-ячейке центрировка всех граней заставляет по-иному выбрать примитивный основной ромбоэдр и соответственно дважды центрированную гексагональную ячейку Браве (рис. 100, в). В результате винтовые оси 31 и 32 оказываются спроектированными на диагональ малого квадрата - ее 1/4 части. При этом с тройными винтовыми осями, перешедшими от Р-ячейки, совпадет лишь четвертая часть из восьми осей 31 и 32 F-решетки, характер которых сохранится.
Таким образом, чтобы нанести на график кубической пространственной группы оси 31 и 32, следует для каждого выхода поворотной оси 3 начертить (обозначить) квадрат со сторонами, равными 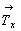 и и 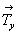 в Р- и I-решетках и в Р- и I-решетках и  и и  - в F-решетке, по отношению к которому исходная ось 3-го порядка занимала бы положение 3[111]. Затем, разделив не проходящую через ось 3 диагональ квадрата на три равные части, найти в соответствии с вышеизложенным правилом позиции осей 31 и 32. На рис. 101 изображено поэтапное получение винтовых осей 31 и 32, сопровождающих каждую из четырех исходных скрещивающихся поворотных осей 3-го порядка в пр. гр. - в F-решетке, по отношению к которому исходная ось 3-го порядка занимала бы положение 3[111]. Затем, разделив не проходящую через ось 3 диагональ квадрата на три равные части, найти в соответствии с вышеизложенным правилом позиции осей 31 и 32. На рис. 101 изображено поэтапное получение винтовых осей 31 и 32, сопровождающих каждую из четырех исходных скрещивающихся поворотных осей 3-го порядка в пр. гр.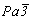 . Окончательный вариант графика пр. гр. . Окончательный вариант графика пр. гр. 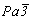 изображен на рис. 96, г. изображен на рис. 96, г.
Пространственная группа Р213 (Т4)
Построение графика пространственной группы Р213, являющейся подгруппой пр. гр. 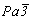 , не должно вызывать затруднений, ибо здесь могут быть использованы рекомендации, сформулированные при построении графика пр. гр. , не должно вызывать затруднений, ибо здесь могут быть использованы рекомендации, сформулированные при построении графика пр. гр. 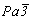 (см. с. 174). А так как исходной в данном случае служит ромбичеcкая осевая пр. гр. Р212121, то вычерчивание искомой группы удобно начать с построения графика именно этой пространственной группы (см. с. 131) с учетом параметров кубической элементарной ячейки (a = b = c). Начало координат, условно выбранное для этой группы в точке, равноудаленной от всех трех скрещивающихся осей 21 (в позиции центра инверсии в пр. гр. (см. с. 174). А так как исходной в данном случае служит ромбичеcкая осевая пр. гр. Р212121, то вычерчивание искомой группы удобно начать с построения графика именно этой пространственной группы (см. с. 131) с учетом параметров кубической элементарной ячейки (a = b = c). Начало координат, условно выбранное для этой группы в точке, равноудаленной от всех трех скрещивающихся осей 21 (в позиции центра инверсии в пр. гр. 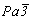 ), служит при ее кубизации местом ввода оси 3-го порядка, ибо только в этом случае осевой комплекс не будет ею размножен (рис. 102, а). Далее поступаем так же, как при выводе пр. гр. ), служит при ее кубизации местом ввода оси 3-го порядка, ибо только в этом случае осевой комплекс не будет ею размножен (рис. 102, а). Далее поступаем так же, как при выводе пр. гр. 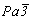 : размножаем введенную ось 3[111] координатными осями 21 (см. с. 175) и наносим на график соответствующие им оси 31 и 32 (рис. 102, б, в). Убеждаемся в том, что полученный осевой комплекс является подгруппой пр. гр. : размножаем введенную ось 3[111] координатными осями 21 (см. с. 175) и наносим на график соответствующие им оси 31 и 32 (рис. 102, б, в). Убеждаемся в том, что полученный осевой комплекс является подгруппой пр. гр. 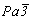 . .
Пространственная группа 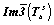
Исходной при построении графика пространственной группы 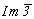 удобно считать группу ромбической голоэдрии Immm, построение которой естественно начать с графика пр. гр. Pmmm, предположив одинаковые параметры элементарной ячейки a, b и с (рис. 103, а). Затем, введя дополнительный трансляционный вектор удобно считать группу ромбической голоэдрии Immm, построение которой естественно начать с графика пр. гр. Pmmm, предположив одинаковые параметры элементарной ячейки a, b и с (рис. 103, а). Затем, введя дополнительный трансляционный вектор 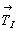 и получив при этом весь комплекс элементов симметрии, чередующихся с исходными Р-группы, можно перейти к пр. гр. Immm (рис. 103, б). После этого следует ввести кубизирующую ось 3-го порядка в точку с максимальной симметрией mmm (точку в начале координат), предварительно убедившись в том, что при этом и осевой и плоскостной комплексы исходной группы останутся неизменными. и получив при этом весь комплекс элементов симметрии, чередующихся с исходными Р-группы, можно перейти к пр. гр. Immm (рис. 103, б). После этого следует ввести кубизирующую ось 3-го порядка в точку с максимальной симметрией mmm (точку в начале координат), предварительно убедившись в том, что при этом и осевой и плоскостной комплексы исходной группы останутся неизменными.
Под действием элементов симметрии исходной группы (например, зеркальных плоскостей симметрии) введенная ось 3[111] будет размножена, т.е. получим три пересекающиеся в одной точке (с координатами 000) оси: 3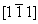 , 3 , 3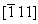 и 3 и 3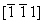 . Далее останется только нанести, воспользовавшись приведенным на с. 175 приемом, оси 31 и 32, всегда сопровождающие в кубической элементарной ячейке поворотные оси 3 (рис. 103, в). . Далее останется только нанести, воспользовавшись приведенным на с. 175 приемом, оси 31 и 32, всегда сопровождающие в кубической элементарной ячейке поворотные оси 3 (рис. 103, в).
Пространственные группы 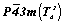 и и 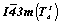
Исходной для построения графика пространственной группы 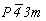 будет тетрагональная группа будет тетрагональная группа 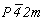 , поэтому и построение графика следует начинать именно с нее. Задание в качестве порождающих элементов симметрии координатной поворотной оси 2-го порядка (2x) и расположенной к ней под углом 45o диагональной зеркальной плоскости (md) обусловит появление инверсионной оси 4-го порядка ( , поэтому и построение графика следует начинать именно с нее. Задание в качестве порождающих элементов симметрии координатной поворотной оси 2-го порядка (2x) и расположенной к ней под углом 45o диагональной зеркальной плоскости (md) обусловит появление инверсионной оси 4-го порядка (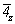 ) (рис. 104, а), взаимодействие которой с трансляциями решетки приведет к появлению еще одной неэквивалентной исходной оси ) (рис. 104, а), взаимодействие которой с трансляциями решетки приведет к появлению еще одной неэквивалентной исходной оси 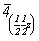 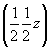 в центре ячейки (см. с. 54). Поворотные оси 2-го порядка, являющиеся подгруппой группы в центре ячейки (см. с. 54). Поворотные оси 2-го порядка, являющиеся подгруппой группы 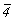 , а также размноженные осью , а также размноженные осью 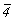 горизонтальные оси 2, взаимодействуя с этими же трансляциями по одинаковому закону, оказываются в позициях на серединах ребер элементарной ячейки. При этом все горизонтальные координатные оси 2 расположатся на двух уровнях (0 и 1/2) по оси Z элементарной ячейки. На графике эта естественная периодичность высот осей, как правило, не отмечается. Из иных высот элементов симметрии указываются только меньшие горизонтальные оси 2, взаимодействуя с этими же трансляциями по одинаковому закону, оказываются в позициях на серединах ребер элементарной ячейки. При этом все горизонтальные координатные оси 2 расположатся на двух уровнях (0 и 1/2) по оси Z элементарной ячейки. На графике эта естественная периодичность высот осей, как правило, не отмечается. Из иных высот элементов симметрии указываются только меньшие 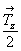 (например, "1/4" подразумевает присутствие оси на высоте не только "1/4", но и "3/4"). Взаимодействие исходной плоскости md с (например, "1/4" подразумевает присутствие оси на высоте не только "1/4", но и "3/4"). Взаимодействие исходной плоскости md с 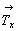 и и 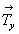 обусловит чередование m (b) (рис. 104, б). обусловит чередование m (b) (рис. 104, б).
В результате всех описанных выше операций симметрии получим график исходной тетрагональной пр. гр. 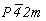 , кубизацию которой можно осуществить вводом оси 3-го порядка, однако при этом следует решить, какой из двух, казалось бы, конкурирующих позиций отдать предпочтение: осевому комплексу 222 в позиции , кубизацию которой можно осуществить вводом оси 3-го порядка, однако при этом следует решить, какой из двух, казалось бы, конкурирующих позиций отдать предпочтение: осевому комплексу 222 в позиции 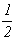 или особой точке инверсионной оси или особой точке инверсионной оси 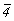 комплекса комплекса 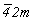 (в начале координат). Введя ось 3[111] в позицию I ( (в начале координат). Введя ось 3[111] в позицию I (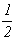 ) (рис. 104, б), увидим, что оси 2-го порядка, пересекающиеся в этой точке, окажутся взаимосвязанными введенной осью 3 (рис. 105, а). При этом единственная ось ) (рис. 104, б), увидим, что оси 2-го порядка, пересекающиеся в этой точке, окажутся взаимосвязанными введенной осью 3 (рис. 105, а). При этом единственная ось 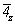 тетрагональной группы размножится поворотом на 120o (рис. 105, б), заняв позиции тетрагональной группы размножится поворотом на 120o (рис. 105, б), заняв позиции 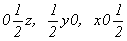 . Размножение каждых двух осей . Размножение каждых двух осей 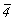 (например, (например, 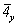 и и 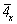 ) третьей - ) третьей - 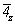 - приведет к тому, что все оси 2-го порядка повысятся до осей - приведет к тому, что все оси 2-го порядка повысятся до осей 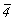 . Действительно, инверсионный поворот оси . Действительно, инверсионный поворот оси 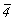 (в позиции (в позиции 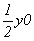 ) вокруг оси ) вокруг оси 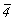 (в позиции (в позиции 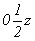 ) даст ось ) даст ось 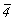 (в позиции x00), которая перекроет существующую в этой позиции ось 2(x00), и т.д. (рис. 105, в). В результате расположения инверсионных осей через 1/2 координатных трансляций вдвое сократятся параметры заданной первоначально элементарной ячейки. (в позиции x00), которая перекроет существующую в этой позиции ось 2(x00), и т.д. (рис. 105, в). В результате расположения инверсионных осей через 1/2 координатных трансляций вдвое сократятся параметры заданной первоначально элементарной ячейки.
Ввод кубизирующей оси 3[111] в позицию II с симметрией 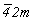 (000) (рис. 105, в) обеспечит круговую перестановку ( (000) (рис. 105, в) обеспечит круговую перестановку ( ) всех осей исходной пространственной группы ) всех осей исходной пространственной группы 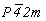 : :
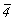 (00z) (00z)  --> --> 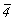 (00z) , (00z) , 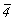 (x00) - в позиции 2(x00) , (x00) - в позиции 2(x00) , 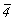 (0y0) - в позиции 2(0y0) , (0y0) - в позиции 2(0y0) ,
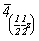 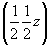  --> --> 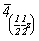 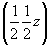 , , 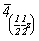 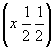 - в позиции 2 - в позиции 2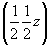 , , 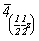 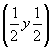 - в позиции 2 - в позиции 2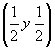 . .
Остальные оси 2-го порядка окажутся связанными кубизирующей осью 3:
2  --> 2 --> 2 , 2 , 2 , 2 , 2 ; ;
2  --> 2 --> 2 , 2 , 2 , 2 , 2 . .
В результате половина исходных осей 2-го порядка войдет в качестве подгрупп в инверсионные оси 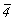 , не сократив при этом размеров исходной элементарной ячейки (см. рис. 104, в). , не сократив при этом размеров исходной элементарной ячейки (см. рис. 104, в).
Следует отметить, что при кубизации инверсионные оси размножаются вместе со своими особыми точками (рис. 106, а) и на графиках кубических пространственных групп изображаются не сами инверсионные оси, а их особые точки (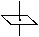 , см. с. 170), в отличие от тетрагональных групп, где инверсионные оси всегда вертикальны и имеют специальное обозначение: , см. с. 170), в отличие от тетрагональных групп, где инверсионные оси всегда вертикальны и имеют специальное обозначение:  . .
На рис. 106, а видно, что из инверсионной оси 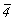 (00z) с особыми точками в позициях 000 и (00z) с особыми точками в позициях 000 и 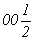 при повороте ( при повороте ( ) вокруг оси 3[111] получим оси ) вокруг оси 3[111] получим оси 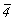 (x00) и (x00) и 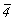 (0y0) с особыми точками, позиции которых легко находят также c помощью круговой перестановки: (0y0) с особыми точками, позиции которых легко находят также c помощью круговой перестановки:
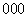  --> --> 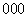 , , 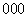 , , 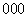 ; ;
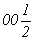  --> --> 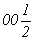 , , 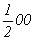 , , 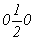
и ось 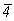 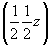  --> --> 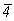 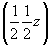 , , 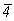 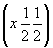 , , 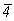 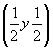 , ,
с особыми точками 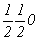  --> --> 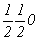 , , 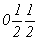 , ,  , ,
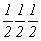  --> --> 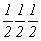 , , 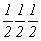 , , 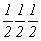 (рис. 106, б). (рис. 106, б).
На графиках (рис. 104, в и 106, д) нанесены найденные позиции особых точек всех инверсионных осей 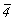 . .
Прием круговой перестановки удобен и для получения всех диагональных плоскостей, связанных осью 3-го порядка. Так, плоскость m(110)  m(110) , m(011) , m(101) , каждая из которых отдельно и все вместе показаны на соответствующем рисунке и графике (рис. 107). При размножении диагональных плоскостей скользящего отражения (в данном случае плоскостей, чередующихся с зеркальными плоскостями) изменение направлений трансляционных компонент меняет соответственно и их наименования. Однако нередко обозначение таких плоскостей буквами, соответствующими скольжению, затруднено. Поэтому в таких случаях удобно воспользоваться нейтральным обозначением: буквой g (нем. gladen - скольжение). В рассматриваемом случае g(110) m(110) , m(011) , m(101) , каждая из которых отдельно и все вместе показаны на соответствующем рисунке и графике (рис. 107). При размножении диагональных плоскостей скользящего отражения (в данном случае плоскостей, чередующихся с зеркальными плоскостями) изменение направлений трансляционных компонент меняет соответственно и их наименования. Однако нередко обозначение таких плоскостей буквами, соответствующими скольжению, затруднено. Поэтому в таких случаях удобно воспользоваться нейтральным обозначением: буквой g (нем. gladen - скольжение). В рассматриваемом случае g(110)  --> g(110) , g(011) , g(101) (рис. 108, а - в). --> g(110) , g(011) , g(101) (рис. 108, а - в).
Последний этап построения графика пространственной группы 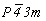 связан с размножением исходной оси 3-го порядка 3[111] комплексом полученных элементов симметрии, а также с локализацией связан с размножением исходной оси 3-го порядка 3[111] комплексом полученных элементов симметрии, а также с локализацией
сопровождающих поворотную ось 3 осей 31 и 32. Сведение воедино всех поэтапно полученных элементов симметрии даст окончательный график пространственной группы (см. рис. 104, г).
Далее естественно получить и график пространственной группы 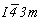 , для чего следует ввести вектор , для чего следует ввести вектор 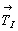 в построенный график пр. гр. в построенный график пр. гр. 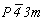 и рассмотреть взаимодействия этого вектора со всеми элементами симметрии группы. Вектор и рассмотреть взаимодействия этого вектора со всеми элементами симметрии группы. Вектор 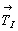 можно ввести уже на этапе вычерчивания графика исходной тетрагональной группы (что легче), т.е. получить сначала группу можно ввести уже на этапе вычерчивания графика исходной тетрагональной группы (что легче), т.е. получить сначала группу 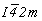 (см. рис. 104, д), а затем ее кубизировать. В обоих случаях построение графика будет включать рассмотрение взаимодействия осей (см. рис. 104, д), а затем ее кубизировать. В обоих случаях построение графика будет включать рассмотрение взаимодействия осей 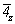 (со своими особыми точками в позициях 000 и (со своими особыми точками в позициях 000 и 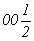 ) и центрирующего объем ячейки вектора, в результате чего возникнут оси того же наименования в центрах квадратов, построенных на горизонтальной составляющей вектора ) и центрирующего объем ячейки вектора, в результате чего возникнут оси того же наименования в центрах квадратов, построенных на горизонтальной составляющей вектора 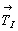 (в позициях (в позициях 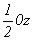 и и 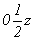 ). При этом изменятся высоты особых точек полученных осей за счет присутствия вертикальной составляющей вектора ). При этом изменятся высоты особых точек полученных осей за счет присутствия вертикальной составляющей вектора 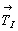 , переносящей особые точки на уровни 1/4 и 3/4 относительно , переносящей особые точки на уровни 1/4 и 3/4 относительно 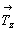 (см. рис. 104, д). (см. рис. 104, д).
Не следует забывать и о том, что центрирующий объем ячейки вектор 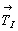 , располагаясь в диагональных плоскостях симметрии m(b), обусловит их тождественность с плоскостями n и с соответственно, т.е. будем иметь m , располагаясь в диагональных плоскостях симметрии m(b), обусловит их тождественность с плоскостями n и с соответственно, т.е. будем иметь m  n (b n (b  c). Однако на окончательном графике тетрагональной пространственной группы изображается лишь одна из каждой пары чередующихся плоскостей: m и с соответственно. Кроме того, вектор c). Однако на окончательном графике тетрагональной пространственной группы изображается лишь одна из каждой пары чередующихся плоскостей: m и с соответственно. Кроме того, вектор 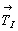 обусловит чередование вертикальных осей 2z = обусловит чередование вертикальных осей 2z = 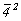 и горизонтальных осей 2x и 2y с винтовыми осями 2-го порядка (см. рис. 104, д). и горизонтальных осей 2x и 2y с винтовыми осями 2-го порядка (см. рис. 104, д).
Дальнейшее построение графика сводится к размножению новых осей 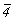 осью 3[111], введенной, как и в рассмотренной выше пр. гр. осью 3[111], введенной, как и в рассмотренной выше пр. гр. 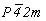 , в позицию (000) с симметрией , в позицию (000) с симметрией 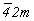 , способом круговой перестановки и нанесению полученных результатов на график: , способом круговой перестановки и нанесению полученных результатов на график:
инверсионная ось  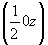  --> -->  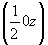 , ,  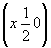 , ,  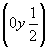
с особыми точками 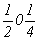  --> --> 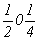 , , 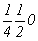 , , 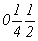 , ,
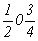  --> --> 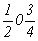 , , 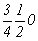 , , 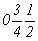 ; ;
инверсионная ось  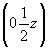  --> -->  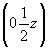 , ,  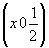 , ,  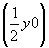
с особыми точками 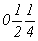  --> --> 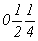 , , 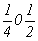 , ,  , ,
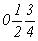  --> --> 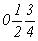 , , 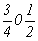 , , 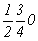
(см. рис. 104, е).
Полный график пространственной группы 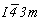 изображен на рис. 104, ж. изображен на рис. 104, ж.
Пространственная группа 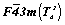
Для того чтобы получить график пространственной группы 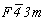 , логично обратиться к тетрагональной группе с F-решеткой - , логично обратиться к тетрагональной группе с F-решеткой - 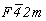 , в стандартной установке соответствующей пр. гр. , в стандартной установке соответствующей пр. гр. 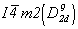 , график которой легко получить на основе пр. гр. , график которой легко получить на основе пр. гр. 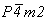 . Таким образом, выстраивается цепочка последовательно вычерчиваемых графиков пространственных групп: . Таким образом, выстраивается цепочка последовательно вычерчиваемых графиков пространственных групп:
 --> --> 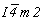 --> --> 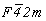 --> --> 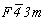 . .
Получение графика тетрагональной пр. гр. 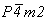 не вызывает затруднений, ибо взятые в качестве порождающих элементов симметрии зеркальная координатная плоскость m и расположенная к ней под углом 45o диагональная ось 2 зафиксируют положение зеркально-поворотной оси не вызывает затруднений, ибо взятые в качестве порождающих элементов симметрии зеркальная координатная плоскость m и расположенная к ней под углом 45o диагональная ось 2 зафиксируют положение зеркально-поворотной оси 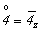 (рис. 109, а) и ее особой точки (в позиции 000). Введение в график этой пространственной группы центрирующего объем ячейки вектора (рис. 109, а) и ее особой точки (в позиции 000). Введение в график этой пространственной группы центрирующего объем ячейки вектора 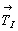 , обеспечит не только чередование исходных зеркальных плоскостей симметрии m с клиноплоскостями n (так же, как и чередование 2(21)), но и появление новых осей , обеспечит не только чередование исходных зеркальных плоскостей симметрии m с клиноплоскостями n (так же, как и чередование 2(21)), но и появление новых осей 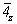 с соответствующими им особыми точками на высоте с соответствующими им особыми точками на высоте 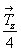 (рис. 109, б). (рис. 109, б).
Для кубизации - перехода к гранецентрированной кубической ячейке - необходимо пр. гр. 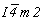 представить в нестандартном для нее F-аспекте: представить в нестандартном для нее F-аспекте: 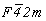 (рис 109, б). При этом координатные и диагональные особые направления поменяются местами. Затем следует ввести кубизирующую ось 3-го порядка в позицию с симметрией (рис 109, б). При этом координатные и диагональные особые направления поменяются местами. Затем следует ввести кубизирующую ось 3-го порядка в позицию с симметрией 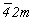 , т.е. в начало координат новой F-ячейки. В результате этого все горизонтальные поворотные оси 2-го порядка повысятся дo , т.е. в начало координат новой F-ячейки. В результате этого все горизонтальные поворотные оси 2-го порядка повысятся дo 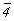 , а также появятся наклонные диагональные плоскости m и n (рис. 109, в): , а также появятся наклонные диагональные плоскости m и n (рис. 109, в):
ось  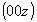  --> -->  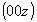 , ,  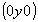 , ,  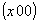
с особыми точками 000  --> 000, 000, 000, --> 000, 000, 000,
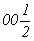  --> --> 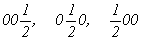 ; ;
ось  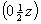  --> -->  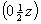 , ,  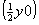 , ,  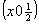
с особыми точками 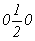  --> --> 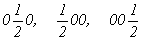 , ,
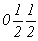  --> -->  ; ;
ось  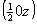  --> -->  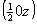 , ,  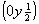 , ,  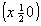
с особыми точками 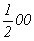  --> --> 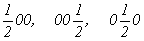 , ,
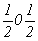  --> --> 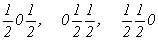 ; ;
ось  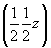  --> -->  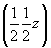 , ,  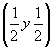 , ,  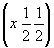
с особыми точками 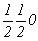  --> --> 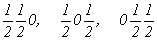 , ,
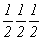  --> --> 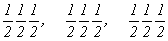 ; ;
ось  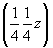  --> -->  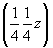 , ,  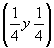 , ,  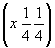
с особыми точками 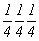  --> --> 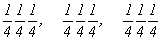 , ,
  --> --> 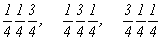 ; ;
ось  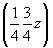  --> -->  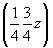 , ,  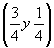 , ,  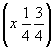
с особыми точками 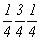  --> --> 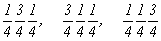 , ,
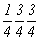  --> --> 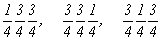 ; ;
ось  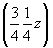  --> -->  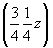 , ,   , ,  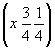
с особыми точками 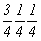  --> --> 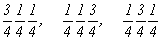 , ,
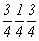  --> -->  ; ;
ось  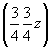  --> -->  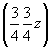 , ,  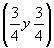 , ,  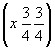
с особыми точками 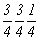  --> --> 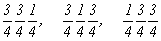 , ,
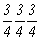  --> --> 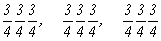 ; ;
плоскости m(110)  --> m(110) , m(101) , m(011) , --> m(110) , m(101) , m(011) ,
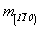  --> --> 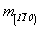 , , 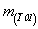 , , 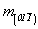 , ,
n(110)  --> n(110) , n(101) , n(011) , --> n(110) , n(101) , n(011) ,
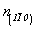  --> --> 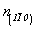 , , 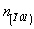 , , 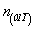 . .
Пространственная группа Р4132 (O7)
Вычерчивание графика пространственной группы Р4132 начинают с построения графика ее тетрагональной подгруппы Р41212. Посчитав порождающими координатную винтовую ось 21(x) и поворотную диагональную ось 2d, отстоящие одна от другой на 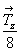 , получим в качестве результирующей ось 41(z) в центре одного из квадратов, построенных на трансляционном векторе оси 21(x). При этом ось 41 окажется в "левом" квадрате, ибо в центре "правого" квадрата она пересечется с исходной ось 2d, что приведет к появлению поворотной координатной оси 2x под углом 45o к 2d, т.е. к невозможному в Р-решетке чередованию координатных осей 21(2) (рис. 110, а). , получим в качестве результирующей ось 41(z) в центре одного из квадратов, построенных на трансляционном векторе оси 21(x). При этом ось 41 окажется в "левом" квадрате, ибо в центре "правого" квадрата она пересечется с исходной ось 2d, что приведет к появлению поворотной координатной оси 2x под углом 45o к 2d, т.е. к невозможному в Р-решетке чередованию координатных осей 21(2) (рис. 110, а).
Далее получаем весь комплекс осей тетрагональной группы:
- за счет взаимодействия 41(z) . 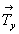 (или (или 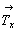 ) получим 41 в центре квадрата, построенного на этой трансляции; ) получим 41 в центре квадрата, построенного на этой трансляции;
- взаимодействие 21(z) (= 412) . 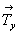 ( (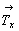 ) приведет к появлению оси 21 на серединах векторов ) приведет к появлению оси 21 на серединах векторов 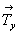 и и 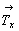 ; ;
- ось 21(x), размноженная осью 41(z) , после поворота на 90o окажется на высоте 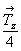 , так же как ось 2d (ее исходная высота , так же как ось 2d (ее исходная высота 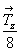 ) - на высоте ) - на высоте 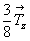 и т.д. (рис. 110, а). и т.д. (рис. 110, а).
Затем переходим к кубизации полученной тетрагональной группы Р41212 . Из двух конкурирующих, казалось бы, позиций (I и II), равноудаленных от всех трех скрещивающихся координатных осей 21 (как в пр. гр. Р213) и всех диагональных осей 2-го порядка, для ввода кубизирующей оси 3-го порядка оказывается пригодной лишь первая, так как только в этом случае при вращении исходных осей 21 и 41 вокруг введенной оси 3[111] не появится новых особых направлений: при этом лишь часть координатных горизонтальных осей 21 будет повышена до 41 (рис. 111, а). При введении же оси 3 в позицию II (см. рис. 110, а) все винтовые горизонтальные координатные оси 2-го порядка повысятся до 4-го порядка, что сократит вдвое параметры исходной элементарной ячейки (рис. 111, б) 1.
Далее, перерисовав график с новым началом координат на оси 3, размножаем сначала ось 3 винтовыми координатными осями 21 (см. с. 173), а затем диагональные оси 2 и 21 способом круговой перестановки и в заключение (рис. 110, б) наносим на график оси 31 и 32 (см. с. 176).
Пространственная группа 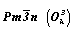
Основой для вычерчивания графика голоэдрической пространственной группы 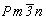 служит ее тетрагональная подгруппа служит ее тетрагональная подгруппа 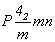 , в стандартном символе которой, приведенном в Интернациональных таблицах, , в стандартном символе которой, приведенном в Интернациональных таблицах, 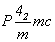 , предпочтение отдано не диагональной клиноплоскости n, а чередующейся с ней плоскости с (с вертикально расположенным трансляционным вектором). Возникновение винтовых осей 42 при взаимодействии вертикальных плоскостей - координатной mx и диагональной сd (с углом 45o между ними) - подтверждается и наличием горизонтальных поворотных осей 2x и 2d, также расположенных под углом 45o , но на высотах, различающихся на 1/4 вертикальной трансляции , предпочтение отдано не диагональной клиноплоскости n, а чередующейся с ней плоскости с (с вертикально расположенным трансляционным вектором). Возникновение винтовых осей 42 при взаимодействии вертикальных плоскостей - координатной mx и диагональной сd (с углом 45o между ними) - подтверждается и наличием горизонтальных поворотных осей 2x и 2d, также расположенных под углом 45o , но на высотах, различающихся на 1/4 вертикальной трансляции 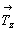 и полученных при взаимодействии вертикальных и горизонтальной плоскостей симметрии: mx . mz = 2x , cd . mz = 2d на и полученных при взаимодействии вертикальных и горизонтальной плоскостей симметрии: mx . mz = 2x , cd . mz = 2d на 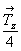 . Взаимодействие диагональных элементов симметрии (сd и 2d) с координатными трансляциями решетки приводит к чередованию cd (nd) и 2d (21(d)). Полный график пр. гр. . Взаимодействие диагональных элементов симметрии (сd и 2d) с координатными трансляциями решетки приводит к чередованию cd (nd) и 2d (21(d)). Полный график пр. гр. 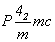 включает и центры инверсии (рис. 112, а). включает и центры инверсии (рис. 112, а).
Из трех позиций с максимальной величиной симметрии (равной 8) : mmm (000), 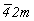 ( (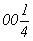 ) и mmm ( ) и mmm ( ) - для введения оси 3-го порядка, повышающей исходную группу ) - для введения оси 3-го порядка, повышающей исходную группу 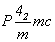 до до 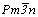 , пригодной оказывается последняя (рис. 112, а), ибо только в этом случае комплекс вертикальных осей останется без изменения, а половина горизонтальных осей 2 повысится до 42: 2 , пригодной оказывается последняя (рис. 112, а), ибо только в этом случае комплекс вертикальных осей останется без изменения, а половина горизонтальных осей 2 повысится до 42: 2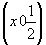 --> 42 --> 42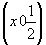 , 21 , 21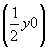 --> 42 --> 42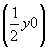 , не сократив при этом параметров исходной элементарной ячейки. При введении оси 3 в другие две указанные позиции все оси 2 повысятся до осей 4-го порядка, что вдвое сократит параметры заданной элементарной ячейки. , не сократив при этом параметров исходной элементарной ячейки. При введении оси 3 в другие две указанные позиции все оси 2 повысятся до осей 4-го порядка, что вдвое сократит параметры заданной элементарной ячейки.
Далее начало координат переносим в выбранную позицию mmm ( ) и наносим винтовые оси 42, размноженные осью 3-го порядка: ) и наносим винтовые оси 42, размноженные осью 3-го порядка:
ось 42  42 42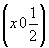 , 42 , 42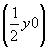 , ,
ось 42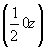  42 42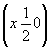 , 42 , 42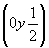 (рис. 112, б). (рис. 112, б).
Совпадающая с осью 42 "невидимая" в исходной пр. гр. 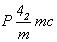 ось ось 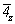 со своими особыми точками, отстоящими от уровня горизонтальной плоскости m (с расположенным в ней центром инверсии) на со своими особыми точками, отстоящими от уровня горизонтальной плоскости m (с расположенным в ней центром инверсии) на  также размножается осью 3. При этом убеждаемся, что оси 42 и также размножается осью 3. При этом убеждаемся, что оси 42 и 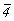 и в кубической группе по-прежнему совпадают: и в кубической группе по-прежнему совпадают:
ось     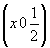 , ,  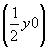
с особыми точками 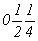  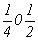 , , 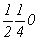 , ,
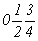  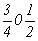 , , 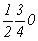 ; ;
ось  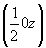   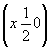 , ,  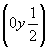 , ,
с особыми точками 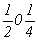  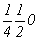 , , 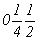 , ,
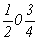  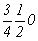 , , 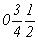 (рис. 112,б). (рис. 112,б).
Особое внимание следует уделить размножению осями 3 диагональных осей 2-го порядка способом круговой перестановки и их обозначению (см. условные обозначения на с. 169). При этом процесс размножения затрагивает как сами оси 2, так и точки их входа (на границах элементарной ячейки).
Например, из диагональной оси 21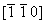 (рис. 113, а), выходящей в точке с координатами (рис. 113, а), выходящей в точке с координатами 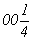 , вращением вокруг оси 3[111] с помощью круговой перестановки получим еще две: , вращением вокруг оси 3[111] с помощью круговой перестановки получим еще две:
ось 21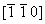  21 21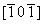 , 21 , 21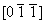
с точкой входа 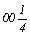  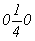 , , 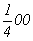 . .
При этом на график (рис. 113, а) наносятся подобно другим наклонным элементам симметрии (см. с. 143) лишь оси 2 или 21 с положительным индексом по оси Z (оси, выходящие с нулевого уровня вверх), т.е. ось 21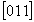 , а не 21 , а не 21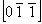 и ось 21 и ось 21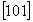 , а не 21 , а не 21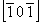 . Если в результате круговой пере-становки точка входа диагональной оси оказыва-ется не на нулевом уровне, то, прежде чем изобразить эту ось на графике, следует найти ее выход на нулевом уровне. . Если в результате круговой пере-становки точка входа диагональной оси оказыва-ется не на нулевом уровне, то, прежде чем изобразить эту ось на графике, следует найти ее выход на нулевом уровне.
Например, при размножении оси 2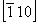  2 2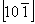 , 2 , 2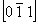 , ,
с точкой входа 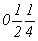  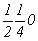 , , 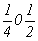
на график (рис. 113, б) ось 2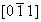 с точкой входа с точкой входа 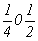 наносится в положении наносится в положении 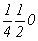 (точка входа на нулевом уровне), ось 2 (точка входа на нулевом уровне), ось 2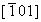 регистрируется своим выходом вверх, т.е. 2 регистрируется своим выходом вверх, т.е. 2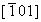 в точке в точке 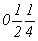 . По предложенной схеме наносим и остальные оси: . По предложенной схеме наносим и остальные оси:
ось 21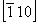  21 21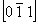 , 21 , 21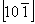
с точкой входа 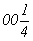  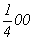 , , 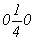 ; ;
ось 2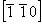  2 2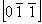 , 2 , 2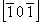 , ,
с точкой входа 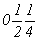  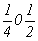 , , 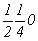 (см. рис. 112, в). (см. рис. 112, в).
Плоскостной комплекс пространственной группы 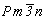 получаем также способом круговой перестановки индексов в символах как координатных, так и диагональных плоскостей. При этом координатные плоскости, перешедшие из тетрагональной группы, здесь оказываются эквивалентными (за счет присутствия равнонаклонной к ним оси 3): получаем также способом круговой перестановки индексов в символах как координатных, так и диагональных плоскостей. При этом координатные плоскости, перешедшие из тетрагональной группы, здесь оказываются эквивалентными (за счет присутствия равнонаклонной к ним оси 3):
mx(100)  my(010) , mz(001). my(010) , mz(001).
Диагональные же плоскости скользящего отражения меняют направления своих трансляционных компонент, а следовательно, и свои наименования и условные обозначения:
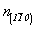  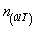 , , 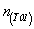 , ,
c(110)  g(011) , g(101) (см. рис. 112, в). g(011) , g(101) (см. рис. 112, в).
Полный график пространственной группы 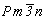 изображен на рис. 112, в. изображен на рис. 112, в.
Пространственная группа 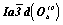
За основу при вычерчивании графика пространственной группы 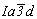 следует взять соответствующую тетрагональную подгруппу следует взять соответствующую тетрагональную подгруппу 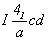 , на второй позиции символа которой координатные плоскости с чередуются за счет присутствия центрирующего объем элементарной ячейки вектора , на второй позиции символа которой координатные плоскости с чередуются за счет присутствия центрирующего объем элементарной ячейки вектора 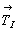 с плоскостями скользящего отражения b и a. Трансляционные компоненты этих плоскостей ( с плоскостями скользящего отражения b и a. Трансляционные компоненты этих плоскостей (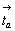 , ,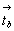 , ,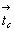 ) направлены вдоль всех трех координатных осей, что позволяет их объединить введенной осью 3[111] на одной (1-й) позиции кубического символа. Таким образом, вычерчивание графика искомой пространственной группы следует начинать с построения графика пр. гр. ) направлены вдоль всех трех координатных осей, что позволяет их объединить введенной осью 3[111] на одной (1-й) позиции кубического символа. Таким образом, вычерчивание графика искомой пространственной группы следует начинать с построения графика пр. гр. 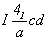 , приняв ее подрешеточный плоскостной комплекс, т.е. плоскости c, b, a, в качестве порождающих элементов симметрии. , приняв ее подрешеточный плоскостной комплекс, т.е. плоскости c, b, a, в качестве порождающих элементов симметрии.
Взаимодействие плоскости сy ( = my . 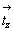 ) и клиноплоскости d (= md . ) и клиноплоскости d (= md . 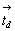 ), расположенных под углом 45o одна к другой (рис. 114, а), обусловит появление винтовой трехзаходной оси 43 в центре квадрата, построенного на горизонтальной составляющей вектора ), расположенных под углом 45o одна к другой (рис. 114, а), обусловит появление винтовой трехзаходной оси 43 в центре квадрата, построенного на горизонтальной составляющей вектора 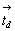 = = 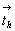 + + 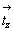 ( где ( где 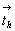 = = 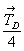 , , 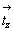 = = 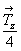 , , 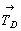 - диагональ грани кубической ячейки). Величину трансляционной компоненты этой оси составят два вертикальных вектора плоскостей с и d: - диагональ грани кубической ячейки). Величину трансляционной компоненты этой оси составят два вертикальных вектора плоскостей с и d: 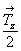 + + 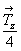 = = 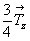 (ср. с взаимодействием my . d, см. с. 158). Проведение симметрических операций в обратном порядке - сначала d, а затем с - обусловит появление также винтовой оси, но уже 41, в центре квадрата, построенного на горизонтальной составляющей, но не исходного (ср. с взаимодействием my . d, см. с. 158). Проведение симметрических операций в обратном порядке - сначала d, а затем с - обусловит появление также винтовой оси, но уже 41, в центре квадрата, построенного на горизонтальной составляющей, но не исходного 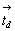 , а ему энантиоморфного вектора (см. с. 68), т.е. отраженного в плоскости my. Таким образом, достаточно задать только две плоскости с и d, чтобы получить чередование осей 41(43), т.е. I-решетку! К этому же типу решетки, как было показано на с. 154, приведет и взаимодействие винтовых осей 41 и 43 с перпендикулярной к ним плоскостью а. Причем помимо вектора , а ему энантиоморфного вектора (см. с. 68), т.е. отраженного в плоскости my. Таким образом, достаточно задать только две плоскости с и d, чтобы получить чередование осей 41(43), т.е. I-решетку! К этому же типу решетки, как было показано на с. 154, приведет и взаимодействие винтовых осей 41 и 43 с перпендикулярной к ним плоскостью а. Причем помимо вектора 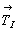 появятся также чередующиеся между собой инверсионные оси появятся также чередующиеся между собой инверсионные оси 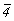 с особыми точками на высотах 1/8 и 3/8 (см. с. 154). с особыми точками на высотах 1/8 и 3/8 (см. с. 154).
Далее не составит труда размножить полученные элементы симметрии, рассмотрев их взаимодействие с трансляциями решетки и друг с другом (и действие друг на друга). При этом следует обратить внимание на то, что винтовые оси 41 и 43 оказываются в квадратах, оконтуренных стрелками клиноплоскостей d, направление которых (стрелок) не совпадает с направлением вращения самих осей (ср. с графиком пр. гр. I41md, где направления вращения осей и стрелок совпадают, см. рис. 92, в), а также на то, что наличие инверсионных осей  и высота их особых точек подтверждается взаимодействием координатных плоскостей симметрии и диагональных осей 2-го порядка (рис. 114, а). и высота их особых точек подтверждается взаимодействием координатных плоскостей симметрии и диагональных осей 2-го порядка (рис. 114, а).
Из четырех позиций без степеней свободы: двух позиций 2 с симметрией 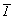 , 222 и , 222 и  приемлемой для ввода кубизирующей оси 3-го порядка будет позиция в центре инверсии, равноудаленном от координатных плоскостей симметрии (так же как в пр. гр. приемлемой для ввода кубизирующей оси 3-го порядка будет позиция в центре инверсии, равноудаленном от координатных плоскостей симметрии (так же как в пр. гр. 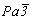 , см. с. 172), ибо только в этом случае они переходят друг в друга, не размножаясь. Вторая система центров инверсии, являющаяся результирующей при взаимодействии с , см. с. 172), ибо только в этом случае они переходят друг в друга, не размножаясь. Вторая система центров инверсии, являющаяся результирующей при взаимодействии с 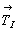 , автоматически окажется расположенной на введенной оси 3[111] , так как она совпадает по направлению с вектором , автоматически окажется расположенной на введенной оси 3[111] , так как она совпадает по направлению с вектором 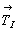 . .
Приведя высоты всех элементов симметрии к выбранному в центре инверсии началу координат, можно приступить к размножению всех элементов симметрии, руководствуясь приведенными выше рекомендациями (рис. 114, б). Полный график искомой пр. гр. 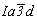 приведен на рис. 114, в. приведен на рис. 114, в.
Пространственная группа 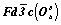
Схема вычерчивания графика данной пространственной группы - 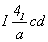 --> --> 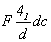 --> --> 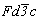 - та же, что и при построении графика пр. - та же, что и при построении графика пр.
гр. 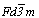 (см. с. 161). Исходной, как и при построении графика пр. гр. (см. с. 161). Исходной, как и при построении графика пр. гр. 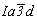 , будет та же пр. гр. , будет та же пр. гр. 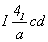 . И отличие заключается лишь в том, что исходная тетрагональная группа должна быть представлена в F-аспекте: . И отличие заключается лишь в том, что исходная тетрагональная группа должна быть представлена в F-аспекте: 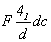 (рис. 115, а). При этом годными к введению кубизирующей оси 3-го порядка оказываются две позиции с симметрией 222 (000) и (рис. 115, а). При этом годными к введению кубизирующей оси 3-го порядка оказываются две позиции с симметрией 222 (000) и 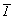 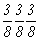 . Действительно, введя ось 3[111] в первую позицию (222), увидим, что на этой оси окажется и вторая позиция с симметрией . Действительно, введя ось 3[111] в первую позицию (222), увидим, что на этой оси окажется и вторая позиция с симметрией 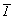 . Поэтому, поскольку оба начала координат в данной кубической группе будут равноценны, в справочной литературе часто приводят два графика этой пространственной группы (рис. 115, б, в). . Поэтому, поскольку оба начала координат в данной кубической группе будут равноценны, в справочной литературе часто приводят два графика этой пространственной группы (рис. 115, б, в).
Пространственная группа 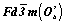
Исходной для вычерчивания графика кубической пространственной группы 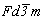 могла бы послужить тетрагональная могла бы послужить тетрагональная 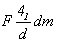 с тремя координатными клиноплоскостями d. Но поскольку ее стандартный аспект с тремя координатными клиноплоскостями d. Но поскольку ее стандартный аспект
соответствует пр. гр. 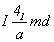 , график удобно начать с построения пр. гр. I41md. Таким образом, последовательность вычерчивания графика искомой , график удобно начать с построения пр. гр. I41md. Таким образом, последовательность вычерчивания графика искомой
пространственной группы будет следующая:
I41md --> 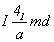 --> --> 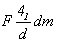 --> --> 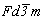 . .
Обратившись к готовому графику пр. гр. 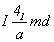 , построение которого приведено на с. 158, и перерисовав его в F-аспекте (рис. 116, а), выбираем позицию для ввода кубизирующей оси 3-го порядка. Для этого пригодными оказываются две взаимосвязанные позиции: точки с симметрией , построение которого приведено на с. 158, и перерисовав его в F-аспекте (рис. 116, а), выбираем позицию для ввода кубизирующей оси 3-го порядка. Для этого пригодными оказываются две взаимосвязанные позиции: точки с симметрией 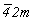 (000) и (000) и 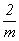 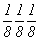 , ибо, введя ось 3[111] в одну из них (например, в особую точку инверсионной оси , ибо, введя ось 3[111] в одну из них (например, в особую точку инверсионной оси 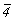 ), автоматически вводим ее и в центр инверсии ( ), автоматически вводим ее и в центр инверсии (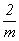 ). Отсюда и два варианта равноправных графиков пр. гр. ). Отсюда и два варианта равноправных графиков пр. гр. 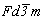 : с началом координат в точке с симметрией : с началом координат в точке с симметрией 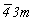 и отстоящей от нее на и отстоящей от нее на 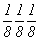 точке с симметрией точке с симметрией 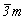 , хотя по традиции предпочтение отдается первой из них. После выбора одного из указанных исходных положений в качестве начала координат построение графика искомой группы не должно вызывать затруднений. Набравшись терпения, следует планомерно размножить все элементы симметрии исходной тетрагональной группы предварительно полученными осями 3-го порядка, используя рекомендации, сформулированные выше. Авторы предлагают читателю проделать это самостоятельно. Окончательные графики пр. гр. , хотя по традиции предпочтение отдается первой из них. После выбора одного из указанных исходных положений в качестве начала координат построение графика искомой группы не должно вызывать затруднений. Набравшись терпения, следует планомерно размножить все элементы симметрии исходной тетрагональной группы предварительно полученными осями 3-го порядка, используя рекомендации, сформулированные выше. Авторы предлагают читателю проделать это самостоятельно. Окончательные графики пр. гр. 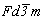 с началом координат в точках с симметрией с началом координат в точках с симметрией 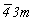 и и 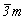 приведены на рис. 116, б и в соответственно. приведены на рис. 116, б и в соответственно.
Геологический факультет МГУ
|


