|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.12. Классный метод вывода пространственных групп гексагональной сингонии
Для сравнения приводим схему классного метода вывода пространственных групп гексагональной сингонии, предложенного Н.В.Беловым [5, 18], уже разобранную при выводе пространственных групп тетрагональной сингонии, также относящихся к средней категории.
Посчитав порождающими в голоэдрических группах гексагональной подсингонии три плоскости симметрии на различных позициях символа и учтя возможность их задания на каждой из позиций, следует рассмотреть их взаимодействия в единственно возможной для этой подсингонии примитивной решетке.
Количество вертикальных плоскостей 2-й и 3-й позиций символа вследствие косоугольности самой элементарной ячейки сократится за счет чередования m(b) и c(n). Взаимодействие указанных вертикальных плоскостей обеих позиций обусловит появление также вертикальной оси 6-го порядка, характер которой будет зависеть от наличия трансляционных компонент в этих плоскостях симметрии. Перпендикулярно осям 6-го порядка может располагаться лишь зеркальная плоскость mz, ибо горизонтальный трансляционный вектор заданной на первой позиции плоскости скользящего отражения неизбежно повторится поворотом вокруг главной оси через 60 и 120o , что приведет к появлению новых трансляционных векторов элементарной ячейки 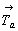 и и 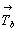 , а также вектора, направленного в центр ее базисной грани ( , а также вектора, направленного в центр ее базисной грани (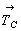 ), т.е. к сокращению координатных трансляций исходной ячейки, в которой заданная плоскость будет "работать" уже как зеркальная. Таким образом, количество групп гексагональной подсингонии с Р-решеткой сократится до четырех по сравнению с 16 пространственными Р-группами тетрагональной голоэдрии: ), т.е. к сокращению координатных трансляций исходной ячейки, в которой заданная плоскость будет "работать" уже как зеркальная. Таким образом, количество групп гексагональной подсингонии с Р-решеткой сократится до четырех по сравнению с 16 пространственными Р-группами тетрагональной голоэдрии:
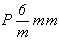 , , 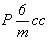 , , 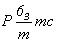 , , 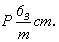
Пространственные группы, подчиненные гемиэдрическим классам 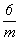 , 6mm, , 6mm, 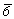 и и 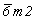 , легко получаются как подгруппы указанных голоэдрических групп: , легко получаются как подгруппы указанных голоэдрических групп:
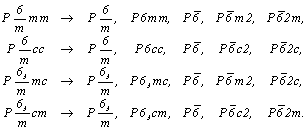
Однако для получения осевых подгрупп класса 622 такой подход c изъятием из голоэдрических групп "лишних" элементов симметрии - элементов симметрии 2-го рода - не годится, поскольку приведет лишь к нейтральным осевым группам Р622 и Р6322, так как энантиоморфные группы не входят в голоэдрические (центросимметричные!) в качестве подгрупп. Поэтому пространственные группы класса D6 получают добавлением к операциям каждой циклической группы класса С6 поворота вокруг оси 2 или 21, перпендикулярной к главному направлению, что приводит ко всем осевым пространственным группам:
Р622, Р6122, Р6222, Р6322, Р6422 и Р6522.
Циклические группы класса С6 легко записать, перечислив все разновидности осей 6-го порядка:
Р6, Р61 , Р62 , Р63 , Р64 , Р65 .
Переходя от собственно гексагональных к пространственным группам тригональной подсингонии, следует иметь в виду, что, во-первых, кроме Р-решетки здесь появляется еще и ромбоэдрическая (R) и, во-вторых, если в гексагональных пространственных группах координатные особые направления неизбежно сопровождаются апофемальными, то в тригональных особые направления могут занимать либо одну, либо другую позицию символа - координатную или апофемальную. При этом если симметрия Р-решетки допускает как одну, так и другую ориентацию особого направления, то расположение узлов R-решетки отвергает элементы симметрии апофемальной позиции. Кроме того, чередование в Р-решетке плоскостей m(b) и с(n) (рис. 121) также сокращает количество голоэдрических групп тригональной подсингонии до трех симморфных: 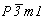 , , 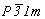 , , 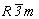 - и трех несимморфных: - и трех несимморфных: 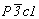 , , 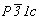 , , 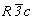 . .
Все остальные группы тригональной подсингонии выводятся из голоэдрических как их подгруппы 1 :
Геологический факультет МГУ
|


