|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IV.6. Взаимодействие поворотной оси симметрии и перпендикулярной к ней трансляции
Результат взаимодействия поворотной оси n-го порядка с перпендикулярной к ней трансляцией 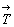  удобно получить, прибегнув к кристаллографическому доказательству [18]. Для этого каждую из взаимодействующих операций симметрии (поворот вокруг оси n и перенос в определенном перпендикулярном к ней направлении) следует заменить отражениями в двух плоскостях. Действительно, последовательные отражения в двух пересекающихся под углом удобно получить, прибегнув к кристаллографическому доказательству [18]. Для этого каждую из взаимодействующих операций симметрии (поворот вокруг оси n и перенос в определенном перпендикулярном к ней направлении) следует заменить отражениями в двух плоскостях. Действительно, последовательные отражения в двух пересекающихся под углом 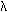 плоскостях симметрии равносильны повороту вокруг линии их пересечения на угол плоскостях симметрии равносильны повороту вокруг линии их пересечения на угол  = 2 = 2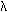 в направлении от плоскости 1-го отражения к плоскости 2-го [20] (см. с. 18). Отсюда поворот вокруг некоторой оси (с элементарным углом поворота a ) можно рассматривать как последовательные отражения в двух плоскостях, пересекающихся вдоль этой оси и расположенных под углом в направлении от плоскости 1-го отражения к плоскости 2-го [20] (см. с. 18). Отсюда поворот вокруг некоторой оси (с элементарным углом поворота a ) можно рассматривать как последовательные отражения в двух плоскостях, пересекающихся вдоль этой оси и расположенных под углом  /2 одна к другой (см. с. 18). Поступание (трансляцию), определяемое некоторым вектором /2 одна к другой (см. с. 18). Поступание (трансляцию), определяемое некоторым вектором 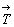 , можно заменить последовательными отражениями в двух параллельных друг другу плоскостях симметрии, перпендикулярных данному вектору и отстоящих одна от другой на половину его длины , можно заменить последовательными отражениями в двух параллельных друг другу плоскостях симметрии, перпендикулярных данному вектору и отстоящих одна от другой на половину его длины 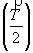 . При этом выбор положения первой плоскости произволен (см. с. 50). . При этом выбор положения первой плоскости произволен (см. с. 50).
Согласно сказанному поворот вокруг оси n, перпендикулярной плоскости чертежа и расположенной в точке О (рис. 29), на угол  (например, против часовой стрелки) заменим последовательными отражениями в перпендикулярных чертежу плоскостях симметрии ОО1 и ОА, образующих угол О1ОА = (например, против часовой стрелки) заменим последовательными отражениями в перпендикулярных чертежу плоскостях симметрии ОО1 и ОА, образующих угол О1ОА =  /2. При этом плоскость второго отражения ОА расположим перпендикулярно вектору /2. При этом плоскость второго отражения ОА расположим перпендикулярно вектору 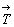 . .
В свою очередь, перенос вдоль вектора 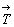 заменим последователь-ными отражениями в двух параллельных плоскостях, перпендикулярных этому вектору: ОА и СО1, при этом ОС = заменим последователь-ными отражениями в двух параллельных плоскостях, перпендикулярных этому вектору: ОА и СО1, при этом ОС = 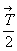 . .
Таким образом, действие оси симметрии и перпендикулярной к ней трансляции мы заменили последовательными отражениями в следующих плоскостях: ОО1 . [ОА . ОА] . CО1 = ОО1 . СО1. Вследствие ассоциативности группового умножения элементов группы ( (gi . gj) * gl = gi * (gj . gl) ) (см. с. 28) можно сначала дважды провести операции отражения в плоскости ОА, взаимно уничтожающие друг друга. Тогда последовательно проведенные две оставшиеся операции отражения в плоскостях ОО1 и СО1 можно заменить поворотом вокруг оси О1 (линии пересечения этих плоскостей). При этом вращение вокруг возникшей оси О1 будет иметь то же направление, что и вокруг исходной оси О. Обратим внимание на то, что при перемножении операций симметрии результат оказывается зависящим от их порядка и потому, когда мы вычеркиваем два отражения в совпадающих плоскостях, необходимо, чтобы эти два отражения стояли рядом в четверке проводимых симметрических операций.
Для того чтобы зафиксировать положение возникшей оси О1 относительно исходной оси О, необходимо определить направление и величину ее сдвига (ОО1), т.е. определить угол СОО1 и расстояние <ОО1> между осями. Из рис. 29 видно, что 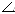 О1ОА = О1ОА = 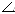 СО1О = СО1О =  / 2 . Из треугольника ОСО1 получаем / 2 . Из треугольника ОСО1 получаем
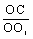 = sin = sin 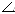 ОО1С, т.е. ОО1С, т.е. 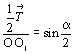 , откуда OO1 , откуда OO1 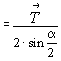 . (12) . (12)
Если рассматривать поворот вокруг исходной оси по часовой стрелке на тот же угол a , то путем подобных рассуждений придем к оси О2 по другую сторону от вектора 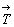 : ОО2 .[ОВ . ОВ] . СО2 = ОО2 . СО2. Если же сначала произвести перенос, а затем поворот, то получим оси О3 и О4. : ОО2 .[ОВ . ОВ] . СО2 = ОО2 . СО2. Если же сначала произвести перенос, а затем поворот, то получим оси О3 и О4.
Подставив в выражение (12) конкретные значения элементарных углов поворота осей различных порядков, получим:
- для оси 2-го порядка ( = 180o ) = 180o )  , т.е. возникшая ось 2 переместится на середину трансляционного вектора , т.е. возникшая ось 2 переместится на середину трансляционного вектора 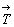 ; ;
- для оси 3-го порядка ( = 120o ) = 120o ) 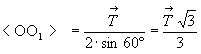 , т.е. возникшая ось 3 переместится в центр равностороннего треугольника, построенного на трансляционном векторе , т.е. возникшая ось 3 переместится в центр равностороннего треугольника, построенного на трансляционном векторе 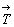 в сторону направления вращения вокруг исходной оси; в сторону направления вращения вокруг исходной оси;
- для оси 4-го порядка ( = 90o ) = 90o ) 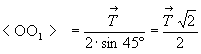 , т.е. возникшая ось 4 окажется в центре квадрата, построенного на векторе , т.е. возникшая ось 4 окажется в центре квадрата, построенного на векторе 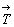 в сторону вращения вокруг исходной оси; в сторону вращения вокруг исходной оси;
- для оси 6-го порядка ( = 60o ) = 60o ) 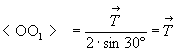 , т.е. возникшая ось 6 будет находиться в центре правильного шестиугольника, построенного также в направлении вращения оси на векторе , т.е. возникшая ось 6 будет находиться в центре правильного шестиугольника, построенного также в направлении вращения оси на векторе 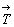 . .
Следует отметить, что если ось высшего порядка содержит в качестве подгруппы оси более низких порядков, то каждая из них взаимодействует с перпендику-лярной трансляцией по своему закону, т.е. попадает в центр правильного многоуголь-ника, соответствующего ее порядку. Например, ось 6-го порядка содержит в качестве состав-ляющих оси 3-го и 2-го порядков. При взаимодействии с координат-ными трансляциями все они "разбегаются" в разные позиции, соответствующие центрам пра-вильных шести-, трех- и двухугольников (рис. 30), что хорошо видно на рисунке Эшера с ящерицами (рис. 31).
Кроме кристаллографического доказательства взаимодействия поворотной оси n-го порядка с перпендикулярной к ней трансляцией 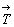 , можно привести и аналитическое [18], которое удобно рассмотреть на примере оси 4-го порядка: 4z . , можно привести и аналитическое [18], которое удобно рассмотреть на примере оси 4-го порядка: 4z . 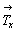 (рис. 32). Для этого в заданной прямоугольной системе координат XYZ, где с осью Z совмещена ось 4(00z), выбираем исходную точку 1 с координатами mnp. Поворот точки 1 по часовой стрелке вокруг вертикальной оси 4z на угол 90o приведет к точке 2 с координатами (рис. 32). Для этого в заданной прямоугольной системе координат XYZ, где с осью Z совмещена ось 4(00z), выбираем исходную точку 1 с координатами mnp. Поворот точки 1 по часовой стрелке вокруг вертикальной оси 4z на угол 90o приведет к точке 2 с координатами 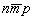 . Последующая симметрическая операция - трансляция . Последующая симметрическая операция - трансляция 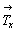 - перенесет точку 2 в положение 3 с координатами - перенесет точку 2 в положение 3 с координатами 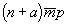 , где a - величина трансляционного вектора , где a - величина трансляционного вектора 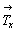 . .
В качестве результата взаимодействия двух операций симметрии 1-го рода (операций поворота и переноса) можно ожидать появление также операции 1-го рода, включающей поворот вокруг другой оси (4') с координатами MNZ, значения которых и предстоит определить.
Для нахождения положения оси 4' выразим координаты точки 1 (mnp) в новой координатной системе, выбранной относительно полученной оси 4' : (m- M)(n- N)p. Поворот вокруг оси 4' (MNZ) изменит координаты точки 1 по тому же закону, что и поворот вокруг исходной оси 4(00z), т.е. получим следующую координату точки 3 в новых осях: (n- N)(M- m)p. Далее пересчитаем координаты точки 3 к исходной координатной системе - (n- N+M)(M- m+N)p. Сравнив последние с ранее полученными 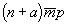 , составим систему уравнений относительно координат М и N: , составим систему уравнений относительно координат М и N:
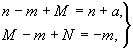
решение которой позволит определить координаты результирующей производной оси 4' : М = a/ 2 и N = - a/ 2 .
Итак, поворот на 90o по часовой стрелке вокруг исходной оси 4-го порядка (4(00z)) и последующая трансляция в перпендикулярном к оси направлении эквивалентны повороту на этот же угол и в том же направлении вокруг производной, неэквивалентной исходной оси 4' , расположенной в центре квадрата, построенного на этой трансляции (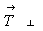 ) по ту ее сторону, в которую ведет поворот. На рис. 33 Эшера хорошо видна неэквивалент-ность исходной и производной осей 4-го порядка: в одной оси 4 сходятся плавники, в другой, порожденной - хвосты рыб. ) по ту ее сторону, в которую ведет поворот. На рис. 33 Эшера хорошо видна неэквивалент-ность исходной и производной осей 4-го порядка: в одной оси 4 сходятся плавники, в другой, порожденной - хвосты рыб.
При рассмотрении взаимодей-ствия осей 3 или 6 с перпенди-кулярной к ним трансляцией возникают затруднения, связанные с существованием третьего горизонтального координатного направления - оси U, а следовательно, и третьей соответствующей этой оси координаты, изъятие которой возможно лишь при условии обращения ее в нуль путем добавления определенной величины ко всем трем значениям координат по горизонтальным осям.
На рис. 34 показано взаимодействие оси 3 с перпендикулярной к ней трансляцией 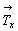 . Рассмотрим перемещение точки 1 с координатами mn0p относительно заданной кристаллографической системы координат (при этом исходная ось 3, совмещенная с координатной осью Z, имеет координаты 000z). Поворот по часовой стрелке на 120o вокруг оси 3 приведет точку 1 к точке 2 с координатами n0mp (круговая перестановка!, см. с. 243). Убрав координату по оси U, т.е. обратив ее в нуль добавлением (- m) ко всем трем координатам по горизонтальным осям, получим . Рассмотрим перемещение точки 1 с координатами mn0p относительно заданной кристаллографической системы координат (при этом исходная ось 3, совмещенная с координатной осью Z, имеет координаты 000z). Поворот по часовой стрелке на 120o вокруг оси 3 приведет точку 1 к точке 2 с координатами n0mp (круговая перестановка!, см. с. 243). Убрав координату по оси U, т.е. обратив ее в нуль добавлением (- m) ко всем трем координатам по горизонтальным осям, получим 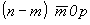 . Трансляция . Трансляция 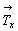 перенесет точку 2 в положение 3 с координатами перенесет точку 2 в положение 3 с координатами 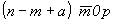 , где a - величина вектора , где a - величина вектора 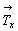 . Далее, выразив положение исходной точки 1 в новых координатных осях (m- M)(n- N)0p (где MN0Z - координаты результирующей оси 3' , связывающей точки 1 и 3) и повернув ее вокруг новой оси 3' , получим точку (n- N)0(m- M)p. После изъятия координаты по третьей горизонтальной оси U имеем координаты (n- N- m+M)(M- m)0p, пересчет которых к исходной координатной системе даст точку (n- N- m+M+M)(M- m+N)0p. Решив систему уравнений . Далее, выразив положение исходной точки 1 в новых координатных осях (m- M)(n- N)0p (где MN0Z - координаты результирующей оси 3' , связывающей точки 1 и 3) и повернув ее вокруг новой оси 3' , получим точку (n- N)0(m- M)p. После изъятия координаты по третьей горизонтальной оси U имеем координаты (n- N- m+M)(M- m)0p, пересчет которых к исходной координатной системе даст точку (n- N- m+M+M)(M- m+N)0p. Решив систему уравнений
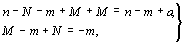
получим значения координат искомой результирующей оси 3' : M = a/3 и N = - a/3, т.е. значения координат центра треугольника, построенного на векторе 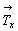 и расположенного от него в сторону рассматриваемого вращения. и расположенного от него в сторону рассматриваемого вращения.
Обобщая два рассмотренных выше примера (4' Т и 3' Т и 3' Т ), можно сделать вывод о том, что взаимодействие оси n-го порядка и перпендикулярной к ней трансляции приводит к появлению результирующей оси того же порядка и типа в центре n-угольника, построенного на трансляционном векторе по ту его сторону, в которую было направлено вращение вокруг исходной оси [19]. ), можно сделать вывод о том, что взаимодействие оси n-го порядка и перпендикулярной к ней трансляции приводит к появлению результирующей оси того же порядка и типа в центре n-угольника, построенного на трансляционном векторе по ту его сторону, в которую было направлено вращение вокруг исходной оси [19].
Таким образом, согласно вышесказанному в качестве результата взаимодействия оси 2-го порядка и 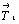 можно ожидать появление еще одной оси 2' на середине трансляционного вектора (в центре "двухугольника"); взаимодействие же оси 6 с можно ожидать появление еще одной оси 2' на середине трансляционного вектора (в центре "двухугольника"); взаимодействие же оси 6 с 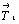 к принципиально новым положениям оси, кроме как размноженным этим вектором, не приведет. Предоставим читателю возможность доказать это самостоятельно. к принципиально новым положениям оси, кроме как размноженным этим вектором, не приведет. Предоставим читателю возможность доказать это самостоятельно.
Схема доказательства во всех случаях одинакова:
1) вначале осуществляется поворот исходной точки вокруг оси, проходящей через начало координат;
2) далее полученная после вращения точка переносится в направлении трансляционного вектора на его величину;
3) координаты исходной точки выражаются в новом координатном репере, выбранном относительно возникшей результирующей оси;
4) точка с полученными координатами размножается по тому же закону, что и точка, повернутая вокруг исходной оси;
5) после этого полученные координаты точки пересчитываются к исходной координатной системе;
6) составляется уравнение относительно координат результирующей оси;
7) решается система уравнений с определением координат результирующей оси.
Все рассуждения относительно взаимодействия поворотной оси и перпендикулярной к ней трансляции справедливы и для осей иного типа: зеркальных, инверсионных или винтовых.
Если трансляционный вектор располагается под углом к исходной вертикальной оси симметрии, отличающимся от 90o , то две составляющие его компоненты - вертикальная и горизонтальная - будут взаимодействовать с осью по разным законам: вертикальный (параллельный оси) вектор вольется в исходную ось, изменив ее характер, второй - перпендикулярный - перенесет возникшую производную ось в центр n-угольника, построенного на этом векторе. В случае взаимодействия вертикальной инверсионной оси с неперпендикулярной к ней трансляцией параллельная этой оси трансляционная компонента изменит высоту особой точки инверсионной оси, переместив ее на свою середину, горизонтальная составляющая по-прежнему перенесет производную инверсионную ось (с иной высотой особой точки!) в центр построенного на ней n-угольника.
Геологический факультет МГУ
|


