Современные модели образования нов и арахноидов можно разделить на два типа - общие геологические, основанные на морфологии этих структур, и геофизические, созданные на базе численного моделирования процессов их образования в зависимости от различных реологических свойств верхних оболочек Венеры. Происхождение нов (Стофан и др., 1992; Сквайрс и др., 1992; Джейнс и др., 1992; и др.) и арахноидов (Марков, Суханов, 1987; Пронин, Бороздин, 1988; Барсуков, Волков, 1989; Никишин и др., 1992; Никишин, 1992; Хэд и др., 1992; Аитолла, Костама, 2001; и др.) связывается с воздействием на верхние части литосферы поднимающихся и испытывающих гравитационную релаксацию мантийных диапиров.
Общие геологические модели
 |
|
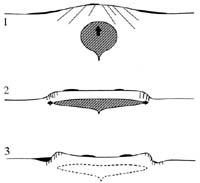
Рис. 12. Основные этапы формирования венцов (Сквайрс и др., 1992).
|
На основании данных КА "Венера 15/16" и "Магеллан" разными авторами (Сквайрс и др., 1992; Джейнс и др., 1992; Стофан и др., 1992, 1997; и др.) была предложена трехэтапная обобщенная модель формирования нов и венцов за счет подъема и релаксации мантийных диапиров. На настоящий момент эта модель является общепринятой (рис. 12):
-
Горячий мантийный диапир поднимается, стремясь достичь своего уровня нейтральной плавучести. Глубина его залегания зависит от температуры поднимающегося материала, его плотности по отношению к вмещающим образованиям и от динамической поддержки диапира. Поднимаясь и механически воздействуя на вышележащие образования, диапир образует над собой радиально-трещиноватый купол воздымания, или нову.
-
Мантийный диапир достигает основания литосферы, что приводит к его латеральному уплощению. Форма поднятия на поверхности трансформируется из куполообразной в платообразную, начинает формироваться венец.
-
Мантийный диапир, охлаждаясь, теряет термическую и динамическую поддержку, что приводит к топографической релаксации поднятия на поверхности, формируются периферийные вал и окружающая его депрессия. Их формирование сопровождается образованием концентрических структур сжатия и растяжения.
Вторая и третья стадии могут частично перекрываться во времени, все стадии сопровождаются вулканическими процессами. В этой модели новы считаются одной из стадий эволюции венцов.
Существует ряд альтернативных моделей образования венцов, предложенных, в основном, на основании данных КА "Венера 15/16" (рис. 3). Модели образования морфоструктур венцов вследствие оползания материала на флангах воздымающегося купола (Барсуков и др., 1984) или вследствие гравитационной модификации поднятия над горячей точкой или магматическим диапиром (Базилевский и др., 1986; Никишин, 1992), не противоречат современной общепринятой модели образования венцов, остальные (рис. 3) были опровергнуты наблюдениями природных структур.
Разница в тектоническом строении арахноидов и нов, а соответственно, и венцов, разными авторами объясняется величиной диапира и его близостью к поверхности (Хэд и др., 1992; Аитолла, Костама, 2001 и др.). Венцы, как структуры большего размера и более активного тектогенеза, образуются при воздействии на верхние части литосферы относительно больших диапиров при их относительно неглубоком залегании (Стофан и др., 1992, 1997; Сквайрс и др., 1992; Джейнс и др., 1992; и др.). Венцы на начальных этапах своего развития проходят стадию образования радиально-трещиноватого купола воздымания - новы, после чего, вследствие гравитационной релаксации постройки, образуется сам венец (Стофан и др., 1992, 1997; Сквайрс и др., 1992; Джейнс и др., 1992; и др.). Арахноиды же образуются вследствие эволюции небольших магматических диапиров при их достаточно глубоком залегании (Хэд и др., 1992; Аитолла, Костама, 2001). Некоторые исследователи (Марков, Суханов, 1987; Барсуков, Волков, 1989; МакКензи и др., 1992; и др.) связывают образование радиальных структур арахноидов, в отдельных случаях связывающих их между собой, с внедрением радиальных роев даек, распределение которых зависит от региональных полей напряжений (МакКензи и др., 1992).
Численные геофизические модели
Воздымание диапира. Для обобщенной модели образования и эволюции венцов, а соответственно, и нов проводилось численное геофизическое моделирование (Стофан и др., 1991; Джейнс и др., 1992; Кох, 1994; Кох, Манга, 1996). Для изучения подъема диапира в мантии и образования возвышенности на поверхности Стофан и др. (1991) использовали расслоенную вязкую модель (Биндшадлер, Парментье, 1990). Значения вязкостей модельной коры и мантии рассчитывались на основе экспериментально полученных данных по реологии диабаза (Шелтон, Туллис, 1981) и оливина (Гётцл, 1978). Диапир рассматривался как аномалия плотности, имеющая осесимметричную форму распределения Гаусса. Исследования показали, что при поднятии диапира с глубины 300 км до 100 км на поверхности образуется поднятие. В этой модели нижняя часть коры имеет меньшие значения вязкости чем верхняя, вследствие чего воздействие диапира частично распределяется в нижней части коры. При применении реологической модели верхних оболочек Венеры Маквела и др. (1993) и Филипса (1997), в которых предполагается менее пластичное состояние нижней части коры, поднятие на поверхности должно быть выражено лучше (Стофан и др., 1991). Формирование купола обуславливает одновременное образование зоны радиального и концентрического растяжения в центральной его части. При этом концентрическое растяжение принимает большие значения, чем радиальное, что должно приводить к образованию радиальных структур растяжения. Поднятие окружено областью, в которой радиальные напряжения принимают характер сжатия, предполагающего образование по периферии концентрических структур сжатия и сдвигов.
 |
|
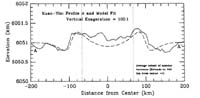
Рис. 13. Топографический профиль через венец Мах.
|
 |
|
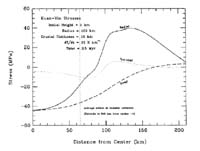
Рис. 14. Напряжения на поверхности для рис. 13.
|
Джейнс и др. (1992) рассматривали реологическую структуру литосферы как слой со свойствами упругости, характерными для базальта, перекрывающий мантию с постоянной вязкостью в соответствии с аналитической моделью Джейнса и Мелоша (1988). Диапир рассматривался как находящееся в мантии множество имеющих положительную плавучесть точек масс в сферической области. При подгонке под реальные топографические профили двух нов (рис. 13) результатов моделирования максимальное соответствие реальных и модельных топографических характеристик было получено при условии поднятия диапира диаметром 90 км, на конечных стадиях находящегося непосредственно под упругой литосферой. Распределение напряжений на поверхности, полученное Джейнсом и др. (1992) (рис. 14), качественно аналогично полученному ранее (Стофан и др., 1991).
Методика подгонки модельных условий к топографии реальных структур неоднозначна, так как модель имеет больше свободных параметров (например, мощность литосферы и коры, размер и глубина залегания диапира, разность плотности вещества диапира и мантии, термический градиент и т.д.) чем можно определить из наблюдений природных структур (например, высота и форма поднятия, распределение радиальных структур растяжения). Тем не менее, Джейнс и др. (1992), применяя эту методику, определили эффективную мощность упругой литосферы при образовании этих двух нов менее чем в 17 км, а положение диапира менее чем в 50 км от основания литосферы. При моделировании радиус диапира был ограничен в пределах от 60 до 110 км. Предполагалось, что воздействие региональных напряжений при этом имеет влияние на распределение деформационных структур, исходя из чего можно определить их характер (Кир, Мелош, 1993).
 |
|
Рис. 15. Топографический профиль через венец Гуань-Инь.
|
 |
|
Рис. 16. Напряжения на поверхности для рис. 15.
|
Уплощение диапира. Форма некоторых венцов платообразная, что объясняется уплощением тела диапира у основания литосферы (Сквайрс и др., 1992, Джейнс и др., 1992). Джейнс и др. (1992) при моделировании топографии одного из венцов (венец Селу) (рис. 15, 16), получили наилучшее соответствие природной и модельной топографической формы этого венца при мощности эластичной литосферы 4 км, разнице плотностей диапира и литосферы 40 кг м-3, радиусе диапира 224 км, вертикальной мощности уплощенного тела диапира 18 км. Поля напряжений, описанные этой моделью, только частично соответствуют распределению тектонических структур наблюдаемому в этом венце и других подобных структурах (Стофан и др., 1997).
Модель Кох (1994) рассматривает движение диапира через мантию с постоянной вязкостью. При его воздействии на основание литосферы также образуется поднятие и радиальная трещиноватость, аналогично описанному выше механизму (Стофан и др., 1991; Джейнс и др., 1992), а сам диапир уплощается в дискообразное тело, трансформируя поднятие в платообразную постройку. При этом ее размеры приблизительно соответствуют размерам диапира. Модель предполагает наличие на краях поднятия обстановки радиального растяжения и вертикального сжатия, что больше соответствует распределению природных тектонических структур (Стофан и др., 1997).
Гравитационная релаксация постройки и тела диапира. Постепенно термическая поддержка диапира уменьшается, само его тело охлаждается и относительно возвышенная постройка становится гравитационно нескомпенсированной, что приводит к ее релаксации. Исследования Стофан и др. (1991) показали, что при гравитационной релаксации платообразного поднятия образуются постройки, схожие с некоторыми венцами - они обладают центральной депрессией и кольцевым валом, окруженным депрессией. Распределение напряжений при этом процессе описано Сквайрсом (1992). Джейнс и Сквайрс (1995) показали, что при гравитационной релаксации образуются преимущественно концентрические структуры растяжения на внешних склонах кольцевого вала венца. Было также подсчитано, что топография венца должна быть лучше выражена и тектонические структуры сильнее развиты при большей мощности коры или повышенном термическом градиенте.
Оценки времени образования новы и ее эволюции в венец. Стофан и др. (1991) основываясь на законе Стокса, показали, что для диапира диаметром 100 км с плотностью на 10 % меньшей, чем плотность мантии, обладающей вязкостью 1021 Па*с, его подъем на величину своего радиуса займет 10 млн. лет. Такому диапиру, находящемуся на глубине 500 км, понадобится 25 млн. лет для достижения приповерхностных областей. Кох (1994) вычислила, что при всех тех же условиях, но вязкости диапира такой же, как у мантии, процесс подъема диапира займет 10 млн. лет, а его уплощение - от 50 до 200 млн. лет. Эти оценки корректны только при условии неизменной вязкости диапира при его уплощении. При этом время остывания диапира при контакте с литосферой, подсчитанное по одномерным моделям (Стофан и др., 1991; Джейнс, Сквайрс, 1995), составляет от 50 до 85 млн. лет. Время гравитационной релаксации модельной постройки при принятых авторами условиях значительно короче, нежели время остывания диапира - от 25000 лет до 1 млн. лет в зависимости от модельной реологической структуры верхних оболочек Венеры. Общее время формирования венца контролируется разными составляющими - временем поднятия диапира, временем его уплощения и временем его остывания. Суммарное время эволюции венца Стофан и др. (1997) оценивают в промежутке от 100 до 250 млн. лет.
Эти численные геофизические модели описывают образование венцов, а следовательно, на начальных стадиях их эволюции, формирование нов (Сквайрс и др., 1992; Джейнс и др., 1992; Стофан и др., 1992, 1997 и др.).
Численные геофизические модели процессов образования арахноидов не предлагались.
|


