|
Автор: Геря Тарас Викторович
диссертация на соискание ученой степени доктора геолого-минералогических наук
Московский Государственный Университет им. М.В. Ломоносова
|
Содержание |
I.5. "Диапир". Численное геодинамическое моделирование.
Уравнения.
При создании системы Диапир мы воспользовались дифференциальными уравнениями, справедливыми для течений несжимаемой вязкой теплопроводящей сплошной среды в поле силы тяжести:
уравнения движения Навье-Стокса:
|
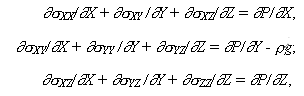
|
(I.5.1)
(I.5.2)
(I.5.3)
|
где
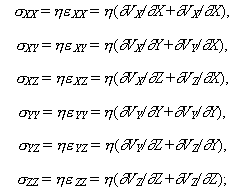
уравнение непрерывности:
|
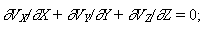
|
(I.5.4)
|
уравнение теплопереноса:
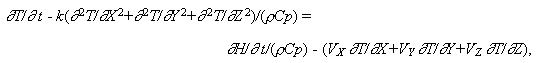 |
(I.5.5)
|
где X и Z - горизонтальные координаты, м; Y - вертикальная координата, м; VX и VZ - горизонтальные скорости, м/с; VY - вертикальная скорость, м/с; 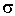 - тензоры вязких напряжений, Па; - тензоры вязких напряжений, Па; 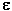 - тензоры скоростей деформаций, 1/с; P - давление, Па; T - температура, К; - тензоры скоростей деформаций, 1/с; P - давление, Па; T - температура, К; 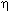 - вязкость, Па.с; - вязкость, Па.с; 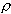 - плотность, кг/м3; g - ускорение силы тяжести, м/с2; t - время, с; k - коэффициент теплопроводности, Вт/(м.К); Cp - изобарная теплоемкость, Дж/(кг.К); дH/дt - теплогенерация, Вт/м3. Теплогенерация за счет вязкого трения, дHo/дt, определяется выражением - плотность, кг/м3; g - ускорение силы тяжести, м/с2; t - время, с; k - коэффициент теплопроводности, Вт/(м.К); Cp - изобарная теплоемкость, Дж/(кг.К); дH/дt - теплогенерация, Вт/м3. Теплогенерация за счет вязкого трения, дHo/дt, определяется выражением
|
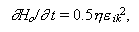
|
(I.5.6)
|
где
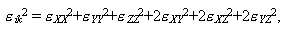
Вязкость 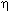 определяется через реологическое уравнение. В данной работе использовалось два типа реологических уравнений определяется через реологическое уравнение. В данной работе использовалось два типа реологических уравнений
|
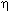 = =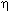 o o
|
(I.5.7)
|
и
|
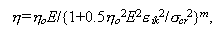
|
(I.5.8)
|
где
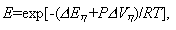
m=(n-1)/(2n),
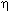 o - константа вязкости, Па.с; o - константа вязкости, Па.с; 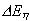 - энергия активации, кал; - энергия активации, кал; 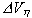 - объем активации, кал/бар; n - константа степенного реологического закона; - объем активации, кал/бар; n - константа степенного реологического закона; 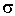 cr - критическое напряжение, Па. Формула (I.5.7) относится к ньютоновской среде, вязкость которой не зависит от внешних параметров. Уравнение (I.5.8) относится к среде с РТ-зависимой реологией. В соответствии с этим уравнением реология является ньютоновской (не зависит от стресса) при напряжениях существенно меньше cr - критическое напряжение, Па. Формула (I.5.7) относится к ньютоновской среде, вязкость которой не зависит от внешних параметров. Уравнение (I.5.8) относится к среде с РТ-зависимой реологией. В соответствии с этим уравнением реология является ньютоновской (не зависит от стресса) при напряжениях существенно меньше 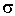 cr и становится степенной (с показателем степени n) при напряжениях намного превышающих cr и становится степенной (с показателем степени n) при напряжениях намного превышающих 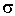 cr (рис. I.11). Уравнение (I.5.8) моделирует реологические свойства мантийного субстрата, который при низких напряжениях характеризуется диффузионной ползучестью а при высоких - дислокационной (Теркот, Шуберт, 1985, стр.542). cr (рис. I.11). Уравнение (I.5.8) моделирует реологические свойства мантийного субстрата, который при низких напряжениях характеризуется диффузионной ползучестью а при высоких - дислокационной (Теркот, Шуберт, 1985, стр.542).
Уравнений (I.5.1)-(I.5.8) записаны для случая трехмерных X-Y-Z течений. Для моделирования двумерных X-Y течений из системы уравнений исключается (I.5.3) а в остальных уравнениях опускаются члены, содержащие Z и VZ.
При моделировании термальной конвекции расчет плотностей пород при заданных Т и Р проводился в соответствии с формулой
|
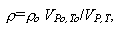
|
(I.5.9)
|
где
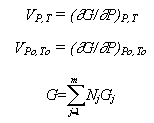
и где 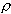 o - плотность породы (кг/м3) при стандартных Po=1 бар и To=298.15 К; VPo,To и VP,T - суммарный объем минералов (кал/бар), слагающих 1 кг породы при стандартных и заданных значениях Т и Р, соответственно; G - суммарный потенциал Гиббса 1 кг породы как функция Т и Р, соответственно; m - число минералов в породе; Nj - число молей j-го минерала в 1 кг породы; Gj - мольный потенциал Гиббса j-го минерала (кал/моль), как функция Т и Р, рассчитанный по формулам, приведенным в разделах I.3 и I.4 настоящей диссертации. o - плотность породы (кг/м3) при стандартных Po=1 бар и To=298.15 К; VPo,To и VP,T - суммарный объем минералов (кал/бар), слагающих 1 кг породы при стандартных и заданных значениях Т и Р, соответственно; G - суммарный потенциал Гиббса 1 кг породы как функция Т и Р, соответственно; m - число минералов в породе; Nj - число молей j-го минерала в 1 кг породы; Gj - мольный потенциал Гиббса j-го минерала (кал/моль), как функция Т и Р, рассчитанный по формулам, приведенным в разделах I.3 и I.4 настоящей диссертации.
Методика численного эксперимента.
Для решения перечисленных уравнений был использован метод конечных разностей на регулярной, прямоугольной, неподвижной (эйлеровой) сетке. Давления расчитывались для центров ячеек а температуры и скорости для узлов сетки. Геометрия счетной области задавалась маркерами, содержащими информацию о физических свойствах пород. Применялась циклическая процедура расчетов с оптимизированным шагом по времени:
а) расчет значений 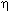 , ,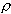 , k и Cp в узлах сетки для текущего момента времени t путем взвешенного осреднения свойств маркеров, находящихся вблизи соответствующих узлов; , k и Cp в узлах сетки для текущего момента времени t путем взвешенного осреднения свойств маркеров, находящихся вблизи соответствующих узлов;
б) определение значений скоростей в узлах сетки и P в центрах ячеек для текущего момента времени t путем итерационного решения уравнений движения и непрерывности с относительной точностью не хуже 10-3; для итерационного расчета давлений использовано уравнение искусственной сжимаемости
|
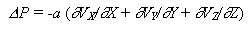
|
(I.5.10)
|
для X-Y-Z течений и
|
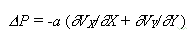
|
(I.5.11)
|
для X-Y течений,
где  P - итерационная поправка к давлению; a - эмпиричиский коэффициент с величиной порядка P - итерационная поправка к давлению; a - эмпиричиский коэффициент с величиной порядка 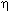 . .
в) определение шага по времени  t через заданные пределы изменения скоростей, температур и позиций маркеров за один шаг по времени; t через заданные пределы изменения скоростей, температур и позиций маркеров за один шаг по времени;
г) определение поля температур для нового момента времени t+ t на основе известных скоростей и температур для текущего момента времени t путем итерационного решения уравнений теплопереноса с относительной точностью не хуже 10-6; при решении использовалась неявная формулировка левой части уравнения теплопереноса и разности против потока в его правой части; t на основе известных скоростей и температур для текущего момента времени t путем итерационного решения уравнений теплопереноса с относительной точностью не хуже 10-6; при решении использовалась неявная формулировка левой части уравнения теплопереноса и разности против потока в его правой части;
д) перемещение маркеров по полю скоростей методом Рунге-Кутта с четвертым порядком точности по координате;
е) переход к новому моменту времени t+ t . t .
Решение всех уравнений базировалось на комбинации метода простой итерации и метода Зейделя с контролем сходимости и относительной точности решения.
Тестирование численных решений.
Тестирование корректности методики численного эксперимента произведено путем сопоставления численных решений с аналитическими для случая двумерных X-Y течений. Затем на основе результатов двумерных численных расчетов была протестирована программа, моделирующая трехмерные X-Y-Z течения. Основной задачей тестовых расчетов была проверка пригодности созданного программного комплекса "Диапир" для моделирования конвективных течений и гравитационного перераспределения пород в земной коре и мантии. Это предполагает корректное численное решение уравнений движения, непрерывности и теплопереноса для сред со сложной реологией в условиях неоднородного распределения плотностей и вязкостей а также значительного градиента температур
Первая серия тестов была проделана для случая неустойчивости Релея-Тейлора в двухслойном разрезе в поле силы тяжести. Геометрия моделируемого разреза показана на рис. I.12. Два слоя равной мощности (H) различались значениями вязкости (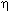 ) и плотности ( ) и плотности (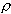 ), причем нижний слой задавался как менее плотный ( ), причем нижний слой задавался как менее плотный (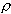 1> 1>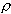 2). На верхней и нижней границах разреза было принято условие прилипания, а на боковых - условие симметрии. На границе слоев задавалось начальное возмущение синусоидальной формы и малой амплитуды (A). Длина волны возмущения ( 2). На верхней и нижней границах разреза было принято условие прилипания, а на боковых - условие симметрии. На границе слоев задавалось начальное возмущение синусоидальной формы и малой амплитуды (A). Длина волны возмущения (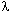 ) отвечала максимальной скорости роста его амплитуды (A) при заданных мощностях (H), вязкостях ( ) отвечала максимальной скорости роста его амплитуды (A) при заданных мощностях (H), вязкостях (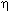 1, 1, 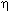 2) и плотностях ( 2) и плотностях (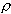 1, 1,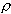 2) слоев ("характеристическая длина волны", Рамберг, 1985). Численно исследовались начальная скорость роста диапира и зависимость его высоты от времени. 2) слоев ("характеристическая длина волны", Рамберг, 1985). Численно исследовались начальная скорость роста диапира и зависимость его высоты от времени.
Сопоставление численных и аналитических (Рамберг, 1985) решений показано на рис.I.13. Как видно из рис.I.13а начальные скорости роста диапира численно определяются правильно, погрешность не превышает +5% и почти не зависит от контраста вязкостей слоев. Это говорит в пользу корректности расчета поля скоростей и давлений и определения эффективных значений физических свойств среды в узлах сетки через свойства маркеров. На рис.I.13б видно совпадение численных и аналитических решений для высоты диапира на начальной стадии его роста для широкого диапазона отношений вязкостей слоев (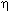 1/ 1/ 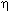 2=0.001-500). Это говорит о правильности численной процедуры изменения геометрии разреза во времени и о корректном лимитировании временного шага. Расхождение численных и аналитических решений на поздних стадиях роста диапира связано в первую очередь с искажением правильности его синусоидальной формы (рис.I.14). Это согласуется с выводом Рамберга (1985) о применимости аналитических решений только для начальных стадий роста диапиров. 2=0.001-500). Это говорит о правильности численной процедуры изменения геометрии разреза во времени и о корректном лимитировании временного шага. Расхождение численных и аналитических решений на поздних стадиях роста диапира связано в первую очередь с искажением правильности его синусоидальной формы (рис.I.14). Это согласуется с выводом Рамберга (1985) о применимости аналитических решений только для начальных стадий роста диапиров.
Вторая серия тестов была проведена для проверки численного решения уравнений теплопереноса. Расчеты проводились для вертикального течения вязкой теплопроводящей среды в канале. Вязкость среды была принята постоянной. В качестве граничных условий задавались вертикальная скорость (VYo) в центре канала на его входе и фиксированные значения температур на неподвижных (условие прилипания) боковых стенках. В качестве начального условия для температур было задано дT/дX=0 и дT/дY=const. Горизонтальный стационарный профиль вертикальных скоростей, VY(X), в таком канале определяется уравнени
|
VY(X) = -4VYo/L2(X2 - LX),
|
(I.5.12)
|
где L - ширина канала, VYo - заданная вертикальная скорость течения в центре канала. Горизонтальные температурные профили через канал для различных моментов времени могут быть получены путем аналитического решения неоднородного уравнения теплопроводности (Тихонов, Самарский, 1972, стр. 214). Для заданных начальных и граничных условий это решение имеет вид
|
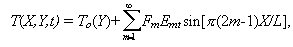
|
(I.5.13)
|
где
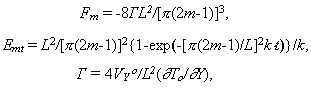
где T(X,Y,t) - температура в канале как функция координат и времени; To(Y) - заданная температура на боковых стенках канала как функция вертикальной координаты; дTo/дY - заданный постоянный градиент температур вдоль боковых стенок канала. Уравнение (I.5.13) не учитывает теплогенерацию за счет вязкого трения, поскольку в соответствии с принятыми начальными и граничными условиями она была незначительной.
На рис.I.15а приведено сопоставление аналитического и численного решений для горизонтального распределения скоростей и температур в канале. На рис.I.15б сравниваются численное и аналитическое решения для зависимости температуры в центре канала от времени. Из диаграмм рис.I.15 видно, что для всех моментов времени численные и аналитические решения для скоростей и тнмператур совпадают. Это свидетельствуют о корректности процедуры численного решения уравнений движения и теплопереноса.
Третья серия тестов была проведена с целью проверки численного решения уравнений движения для среды со степенной реологией в условиях градиента температур. Расчеты проводились для вертикального течения вязкой теплопроводящей среды в канале. В качестве граничных условий задавались вертикальная скорость (VYo) в центре канала на его входе, условие прилипания на неподвижных боковых стенках и фиксированное горизонтальное распределение температур (рис.I.16а), отвечавшее уравнению
|
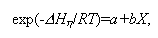
|
(I.5.14)
|
где
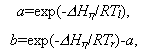
где Tl и Tr - значения температур на левой и правой стенках канала, соответственно. Для вертикального распределения температур было принято условие дT/дY=0. Вязкость задавалась уравнением (I.5.8) с n=3. При этом исследовались два крайних случая (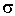 cr>> cr>>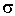 XY) и ( XY) и (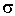 cr<< cr<<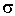 XY), которым с учетом (I.5.8) отвечают два упрощенных реологических уравнения XY), которым с учетом (I.5.8) отвечают два упрощенных реологических уравнения
|
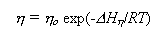
|
(I.5.15)
|
и
|

|
(I.5.16)
|
соответственно. Аналитические решения для горизонтального профиля вертикальных скоростей в канале для этих двух случаев будут иметь вид, соответственно
|
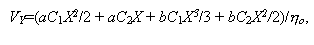
|
(I.5.17)
|
и
|
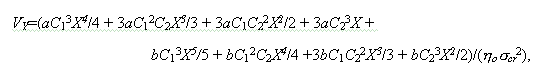
|
(I.5.18)
|
где C1 и C2 - коэффициенты, заданные таким образом, чтобы вертикальная скорость на стенках канала была равна нулю а в центре канала имела значение VYo.
На рис.I.16б приведено сопоставление аналитических и численных решений для горизонтального распределения скоростей в канале. Видно, что для обоих рассмотренных случаев численные и аналитические решения совпадают. Это свидетельствуют о корректности процедуры численного решения уравнений движения для среды со сложной реологией вида (I.5.8) при наличии градиента температур.
В целом результаты теста показали, что методика численного эксперимента является корректной а разработанный программный комплекс "Диапир" может быть успешно использован для моделирования конвективных течений и гравитационного перераспределения пород в земной коре и мантии.
Моделирование Р-Т трендов.
Р-Т тренд непосредственно фиксирует перемещение (физическую траекторию) породы в земной коре в ходе процессов регионального метаморфизма. Именно поэтому Р-Т тренды являются важным инструментом познания многих геодинамических процессов. За последние 25 лет Р-Т тренды были получены для огромного числа самых разнообразных метаморфических комплексов (см. обзор Spear, 1993). Одномерное геодинамической моделирование Р-Т трендов регионального метаморфизма в рамках коллизионно-эрозионной модели (England & Tompson, 1984) позволило понять многие общие закономерности Р-Т эволюции метаморфических пород, однако в силу значительной упрощенности не могло учесть всю специфику геодинамической истории реальных комплексов. Очевидно, что дальнейший прогресс в этом направлении может быть связан с исследованием более сложных двух- и трехмерных численных геодинамических моделей. Это особенно важно для познания закономерностей пространственного распределения пород, испытавших различную Р-Т эволюцию в ходе единого геодинамического процесса. Наличие таких пород подтверждается детальными петрологическими исследованиями некоторых метаморфических комплексов (например, Perchuk et al., 1989, 1996) (см. также Главу III).
Система "Диапир" позволяет производить моделирование Р-Т трендов путем интерполяционного расчета температур и давлений для заданных маркеров в заданные моменты времени (Gerya et. al., 1999). Это позволяет исследовать как характер трендов, так и их распределение в модельном разрезе. Сопоставление модельных Р-Т трендов с результатами геотермобарометрии для конкретных комплексов создает возможность дополнительного контроля корректности численных моделей.
Согласование модельных Р-Т трендов с эмпирическими путем подбора эффективных вязкостей пород (Gerya et. al., 1999) позволяет оценить длительность процессов гравитационного перераспределения для конкретных комплексов. В отличие от достаточно хорошо известных плотностей, теплоемкостей и теплопроводностей различных горных пород их вязкости изучены недостаточно и варьируют в очень широких пределах. С этой точки зрения согласование Р-Т трендов является перспективной методикой уточнения реологии горных пород в различных геодинамических процессах. Использование такого согласования при оценке эффективных вязкостей и скоростей подъема гранулитов проиллюстрировано в главе IV.
| Полные данные о работе |
Геологический факультет МГУ |
|


