|
Автор: Геря Тарас Викторович
диссертация на соискание ученой степени доктора геолого-минералогических наук
Московский Государственный Университет им. М.В. Ломоносова
|
Содержание |
I.3. "ГеоПас". База данных. Уравнения потенциала Гиббса для минералов и сжатых газов.
Потенциал Гиббса является базовой функцией для определения термодинамических свойств веществ при заданных Т и Р и его функциональная форма играет значительную роль при моделировании фазовых равновесий в широком интервале температур и давлений. Термодинамические базы данных, использующиеся в петрологии, традиционно (например, Карпов и др., 1976; Berman, 1988; Holland & Powell, 1990, 1998) используют формулировку потенциала Гиббса через температурные и барические зависимости объемов и теплоемкостей фаз в виде
 G(P,T) = G(P,T) =  Ho - T.So + Ho - T.So +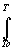 [Cpo(T)]dT - T. [Cpo(T)]dT - T. 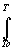 [Cpo(T)/T]dT + [Cpo(T)/T]dT + 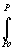 [V(P,T)]dP, [V(P,T)]dP,
где G(P,T) - мольная энергия Гиббса при заданных Р и Т;  Ho и So - соответственно энтальпия образования и энтропия вещества при стандартных температуре То и давлении Ро; Cpo(T) - зависимость теплоемкости вещества от температуры при стандартном давлении Ро; V(P,T) - зависимость объема вещества от температуры и давления. Вид функций Cpo(T) и V(P,T)) подбирается эмпирически и обычно задается в виде степенных полиномов, позволяющих для многих минералов с достаточно высокой точностью воспроизвести экспериментальные данные по фазовым равновесиям и/или термохимическим определениям, однако вызывает заметные трудности при экстраполяции термодинамических свойств веществ до высоких температур и давлений (например, Richet et al., 1992; Saxena et al., 1993). Трудности создания и оптимизации взаимосогласованных баз термодинамических данных для петрологии часто связаны с проблемой выбора тех или иных полиномиальных выражений для описания теплоемкости, объема, термической расширяемости и сжимаемости минералов и флюидов. Во многих случаях, в особенности для флюидов, это предполагает использование большого числа эмпирических коэффициентов. При этом часто для описания одних и тех же термодинамических свойств в разных интервалах температуры и давления используются различные уравнения (например, Belonozshko et al., 1992; Holland & Powell, 1998). Ho и So - соответственно энтальпия образования и энтропия вещества при стандартных температуре То и давлении Ро; Cpo(T) - зависимость теплоемкости вещества от температуры при стандартном давлении Ро; V(P,T) - зависимость объема вещества от температуры и давления. Вид функций Cpo(T) и V(P,T)) подбирается эмпирически и обычно задается в виде степенных полиномов, позволяющих для многих минералов с достаточно высокой точностью воспроизвести экспериментальные данные по фазовым равновесиям и/или термохимическим определениям, однако вызывает заметные трудности при экстраполяции термодинамических свойств веществ до высоких температур и давлений (например, Richet et al., 1992; Saxena et al., 1993). Трудности создания и оптимизации взаимосогласованных баз термодинамических данных для петрологии часто связаны с проблемой выбора тех или иных полиномиальных выражений для описания теплоемкости, объема, термической расширяемости и сжимаемости минералов и флюидов. Во многих случаях, в особенности для флюидов, это предполагает использование большого числа эмпирических коэффициентов. При этом часто для описания одних и тех же термодинамических свойств в разных интервалах температуры и давления используются различные уравнения (например, Belonozshko et al., 1992; Holland & Powell, 1998).
Если в качестве базовой функции используется потенциал Гельмгольца минералов (например, Kieffer, 1985; Поляков и Кусков, 1994) и флюидов (например, Stewart & Jacobson, 1989; Saul & Wagner, 1989; Hill, 1990), расчет потенциала Гиббса через известное соотношение G = F - V.дF/дV требует промежуточных итераций и создает определенные трудности при решении петрологических задач.
Формы выражений для потенциала Гиббса минералов и флюидов обычно сильно различаются, что является следствием существенно разных подходов применяемых при их выводе. Тем не менее, в теории Ландау (Ландау и Лифшиц, 1995) доказана аналогия описания термодинамических свойств кристаллических фаз в области 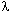 -перехода и флюидов в области критической точки. Потенциал Гиббса таких фаз может быть рассмотрен как функция температуры, давления и параметра порядка -перехода и флюидов в области критической точки. Потенциал Гиббса таких фаз может быть рассмотрен как функция температуры, давления и параметра порядка 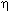 . При этом равновесное значение параметра порядка отвечает минимуму Энергии Гиббса при заданных Р и Т . При этом равновесное значение параметра порядка отвечает минимуму Энергии Гиббса при заданных Р и Т
|
G(T,P,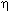 ) = min. ) = min.
|
(I.3.1)
|
Концепция Томпсона (Thompson, 1969) также предполагает аналогию внутрифазных равновесий во флюидном и кристаллическом состояниях. Однако, в то время как для кристаллических фаз теория Ландау и подход Томпсона активно используются (например, Holland & Powell, 1996, 1998; Dove, 1997), они не слишком широко применяются при описании термодинамических свойств однокомпонентных флюидов. Все же следует отметить, что концепция внутрифазных реакций ассоциирования молекул хорошо разработана для флюидов с водородным типом межмолекулярных связей (например, Luck, 1980; Gupta et al., 1992). Кроме того, потенциальная применимость концепции внутренних цепных реакций кластеризации показана для любых надкритических газов (Барелко и др., 1995). Развивая эти подходы, ассоциация молекул однокомпонентного флюида (включая переход газ-жидкость) может рассматриваться в рамках подходов Ландау и Томпсона как специфический тип процесса упорядочения. Наши исследования (Gerya & Perchuk, 1997a; Gerya et al., 1998) показали, что на этой основе могут быть получены достаточно компактные выражения, описывающие потенциала Гиббса минералов и флюидов в широком интервале Р-Т параметров. При этом вибрационная часть потенциала Гиббса выводится на основе статистической суммы для T-P распределения (Богуславский, 1961; Кубо, 1967), а конфигурационная выражается с использованием концепции внутрифазового равновесия (Thompson, 1969). Ниже приводится обобщенный вывод этих выражений и показывается их применимость для описания и экстраполяции термодинамических свойств минералов и флюидов.
Энергия Гиббса фазы в состоянии термодинамического равновесия
Вибрационная часть потенциала Гиббса
Рассмотрим сначала вещество в конденсированном состоянии, твердом или жидком, при относительно низкой температуре, когда его атомы сближены и в основном колеблются вблизи положений равновесия. Система из N атомов будет иметь 3N степеней свободы и с точки зрения статистической механики может рассматриваться как система 3N независимых квантовых осцилляторов (например, Ландау и Лифшиц, 1995). Для данной системы традиционно рассматривается канонический (T-V) ансамбль (например, Кубо, 1967), и каноническая статистическая сумма используется для вывода выражений для потенциала Гельмгольца. Энергия Гиббса различных фаз при этом выражается с использованием вычисленных канонических сумм, например, в форме G = F + PV (Кубо, 1967). В этом случае давление вычисляется через известное термодинамическое соотношение P = -дF/дV, что даже для простых кристаллических фаз предполагает использование итерационной процедуры для расчета потенциала Гиббса при заданных Р и Т. Поскольку для петрологических задач предпочтительна прямая формулировка потенциала Гиббса как функции Р и Т, ниже мы попытаемся решить эту задачу.
Потенциал Гиббса системы квантовых осцилляторов при постоянных Т и Р может быть выражен на основе T-P распределения (Богуславский, 1961; Кубо, 1967)
|
где Y=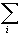 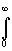 exp{-[Ei(V)+PV]/ kBT} dV. exp{-[Ei(V)+PV]/ kBT} dV.
|
(I.3.3)
|
Y - статистическая сумма, kB - константа Больцмана, V - объем системы, и Ei(V) - энергия системы в i-том квантовом состоянии как функция объема. Теоретические выражения для Ei(V) отсутствуют и взамен используются различные полуэмпирические формулировки. Если в i-том квантовом состоянии при заданном давлении P только один объем системы имеет ненулевую вероятность, тогда
|
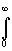 exp{-[Ei(V)+PV]/kBT}dV = exp[-Hi(P)/kBT], exp{-[Ei(V)+PV]/kBT}dV = exp[-Hi(P)/kBT],
|
(I.3.4)
|
где Hi(P) = Ei(P)+PVi(P) и Ei(P)= Ei[Vi(P)]. Hi(P), Ei(P), и Vi(P) - энтальпия (или, точнее, ее микроскопический аналог), энергия и объем системы, соответственно, в i-том квантовом состоянии как функции Р. Введем эффективные объем Vi(P) и соответствующие ему Hi(P) и Ei(P), делающие уравнение (I.3.4) справедливым для случая, когда в i-том квантовом состоянии возможны малые флуктуации объема системы V относительно Vi(P). Тогда уравнение (I.3.3) может быть упрощено до вида
|
Y= 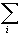 exp[-Hi(P)/kBT]. exp[-Hi(P)/kBT].
|
(I.3.5)
|
Предположение о малости флуктуаций объема в конденсированном состоянии оправдано, поскольку распределение плотности вероятности по объему в этом состоянии имеет очень узкий максимум (Hill, 1956).
Нормализуя функцию распределения относительно состояния нулевых колебаний, получаем
|
G = G0(P) - kBTln(Y0),
|
(I.3.6)
|
где Y0 = 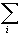 exp[- exp[- Hi(P)/ kBT], G0 = H0(P) - TS0, Hi(P)/ kBT], G0 = H0(P) - TS0,
 Hi(P)= Hi(P) - H0(P) = Ei(P) + P Hi(P)= Hi(P) - H0(P) = Ei(P) + P Vi(P) , Vi(P) ,
H0(P) = E0(P) + PV0(P),  Ei(P)= Ei(P) - E0(P), Ei(P)= Ei(P) - E0(P),  Vi(P) = Vi(P) - V0(P). Vi(P) = Vi(P) - V0(P).
Y0 - статистическая сумма, нормализованная относительно состояния нулевых колебаний. G0(P), H0(P), E0(P), и V0(P) - соответственно, энергия Гиббса, энтальпия, энергия и объем системы в состоянии нулевых колебаний как функции Р. S0 - энтропия системы в состоянии нулевых колебаний (для упорядоченных кристаллических фаз в соответствии с законом Нернста S0=0).  Hi(P), Hi(P),  Ei(P) и Ei(P) и  Vi(P) - соответственно, энтальпийный, энергетический и объемный эффекты перехода системы из состояния нулевых колебаний в i-тое квантовое состояние как функции Р. Учитывая 3N независимых осцилляторов получим: Vi(P) - соответственно, энтальпийный, энергетический и объемный эффекты перехода системы из состояния нулевых колебаний в i-тое квантовое состояние как функции Р. Учитывая 3N независимых осцилляторов получим:
|
Y0 =  Y0i , Y0i ,
|
(I.3.7)
|
где Y0i =  exp[- exp[- Hij(P)/kBT], Hij(P)/kBT],  Hij(P) = Hij(P) =  Eij(P) + P Eij(P) + P Vij(P). Vij(P).
Y0i - статистическая сумма для i-того осциллятора нормализованная относительно состояния нулевых колебаний, M - число энергетических уровней для i-того осциллятора,  Hij(P) , Hij(P) ,  Eij(P) и Eij(P) и  Vij(P) - соответственно, энтальпийный, энергетический и объемный эффекты связанные с переходом i-того осциллятора из состояния нулевых колебаний на j-тый энергетический уровень как функции Р. Для вычисления Y0i, примем, что каждый осциллятор имеет бесконечное число энергетических уровней (например, Ландау и Лифшиц, 1995) и что Vij(P) - соответственно, энтальпийный, энергетический и объемный эффекты связанные с переходом i-того осциллятора из состояния нулевых колебаний на j-тый энергетический уровень как функции Р. Для вычисления Y0i, примем, что каждый осциллятор имеет бесконечное число энергетических уровней (например, Ландау и Лифшиц, 1995) и что  Hij(P), Hij(P),  Eij(P) и Eij(P) и  Vij(P) пропорциональны j. Тогда Vij(P) пропорциональны j. Тогда
|
 Hij(P) = j. Hij(P) = j. Hi0(P) Hi0(P)
|
(I.3.8)
|
и
|
Y0i = 1/{1 - exp[- Hi0(P) /kBT]}, Hi0(P) /kBT]},
|
(I.3.9)
|
где  Hi0(P) = Hi0(P) =  Ei0(P) + Ei0(P) +  Vi0(P). Vi0(P).
 Hi0(P), Hi0(P),  Ei0(P), and Ei0(P), and  Vi0(P) - соответственно, энтальпийный, энергетический и объемный эффекты связанные с переходом i-того осциллятора между соседними энергетическими уровнями как функции Р. В соответствии с (I.3.8) и (I.3.9) увеличение объема системы при повышении температуры в условиях постоянства внешнего давления пропорционально увеличению числа фононов. Это изменение объема компенсирует увеличение теплового давления, которое также пропорционально возрастанию количества фононов. Таким образом, формулы (I.3.8) и (I.3.9) являются физически оправданными. Преобразуя (I.3.6) с учетом (I.3.9), запишем Vi0(P) - соответственно, энтальпийный, энергетический и объемный эффекты связанные с переходом i-того осциллятора между соседними энергетическими уровнями как функции Р. В соответствии с (I.3.8) и (I.3.9) увеличение объема системы при повышении температуры в условиях постоянства внешнего давления пропорционально увеличению числа фононов. Это изменение объема компенсирует увеличение теплового давления, которое также пропорционально возрастанию количества фононов. Таким образом, формулы (I.3.8) и (I.3.9) являются физически оправданными. Преобразуя (I.3.6) с учетом (I.3.9), запишем
|
G = H0(P) - TS0 + kBT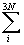 ln{1-exp[- ln{1-exp[- Hi0(P)/kBT]}. Hi0(P)/kBT]}.
|
(I.3.10)
|
Если N =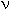 NA (где NA - число Авогадро и NA (где NA - число Авогадро и 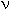 - число атомов в элементарной ячейке вещества) и значения - число атомов в элементарной ячейке вещества) и значения  Hi0 для больших групп осцилляторов одинаковы во всем диапазоне давлений, уравнение (I.3.10) может быть переписано в виде Hi0 для больших групп осцилляторов одинаковы во всем диапазоне давлений, уравнение (I.3.10) может быть переписано в виде
|
Gs = Hs - TSso +RT 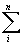 ci ln{1-exp[- ci ln{1-exp[- Hsi/RT]}, Hsi/RT]},
|
(I.3.11)
|
где Hs и Sso - соответственно, мольная энтальпия и энтропия в состоянии нулевых колебаний (Sso полагается независимым от P), n - число групп осцилляторов, характеризующихся различными  Hi0, ci - статистический вес i-той группы осцилляторов равный числу осцилляторов в i-той группе деленному на NA, Hi0, ci - статистический вес i-той группы осцилляторов равный числу осцилляторов в i-той группе деленному на NA,  Hsi - энтальпийный эффект перехода между соседними энергетическими уровнями для i-той группы осцилляторов в расчете на NA осцилляторов (т.е. Hsi - энтальпийный эффект перехода между соседними энергетическими уровнями для i-той группы осцилляторов в расчете на NA осцилляторов (т.е.  Hsi=NA Hsi=NA Hi0). Форма уравнения (I.3.11) напоминает стандартное выражение для потенциала Гельмгольца системы независимых осцилляторов (например, Ландау и Лифшиц, 1995, Кубо, 1967, Toda et al. 1992), однако главное отличие состоит в том, что статистическая сумма выражены через энтальпийные (а не энергетические) эффекты переходов осцилляторов. Hi0). Форма уравнения (I.3.11) напоминает стандартное выражение для потенциала Гельмгольца системы независимых осцилляторов (например, Ландау и Лифшиц, 1995, Кубо, 1967, Toda et al. 1992), однако главное отличие состоит в том, что статистическая сумма выражены через энтальпийные (а не энергетические) эффекты переходов осцилляторов.
Зависимость Hs и  Hs от давления может быть записана в виде Hs от давления может быть записана в виде
|
Hs = Hso + 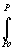 VsdP VsdP
|
(I.3.12)
|
и
где Po - стандартное давление, Hso - мольная энтальпия при 0, K и Po,  Hsio - величина Hsio - величина  Hsi при o, Vs - мольный объем при 0, K как функция давления, Hsi при o, Vs - мольный объем при 0, K как функция давления,  Vsi - объемный эффект, связанный с переходом между соседними энергетическими уровнями для i-той группы осцилляторов как функция давления (также в расчете на NA осцилляторов). Таким образом, уравнения (I.3.11) - (I.3.13) прямо выражают потенциал Гиббса системы независимых осцилляторов как функцию Р и Т. Vsi - объемный эффект, связанный с переходом между соседними энергетическими уровнями для i-той группы осцилляторов как функция давления (также в расчете на NA осцилляторов). Таким образом, уравнения (I.3.11) - (I.3.13) прямо выражают потенциал Гиббса системы независимых осцилляторов как функцию Р и Т.
Для состояния нулевых колебаний можно предположить что зависимость объема системы Vs от P отвечает уравнению Мурнагана, которое часто используется для описания изотермических зависимостей объемов конденсированных (особенно, кристаллических) фаз от давления. Тогда
|
Vs = Vso (Po +  )1/5 / (P + )1/5 / (P +  )1/5, )1/5,
|
(I.3.14)
|
где Vso - мольный объем при 0 K и Po,  - параметр обобщенно характеризующий силы межатомного притяжения во всем интервале давлений. Показатель степени 1/5 принят в соответствии с предположением, что потенциальная энергия сил отталкивания атомов пропорциональна 4-той степени их эффективного объема. В общем случае формы выражений - параметр обобщенно характеризующий силы межатомного притяжения во всем интервале давлений. Показатель степени 1/5 принят в соответствии с предположением, что потенциальная энергия сил отталкивания атомов пропорциональна 4-той степени их эффективного объема. В общем случае формы выражений  Vsi и Vs различаются. Однако, учитывая, что Vsi и Vs различаются. Однако, учитывая, что  Vsi <<Vs, выразим Vsi <<Vs, выразим  Vsi в форме аналогичной (I.3.14) Vsi в форме аналогичной (I.3.14)
где  Vsio - величина Vsio - величина  Vsi при Po. В соответствии с (I.3.12)-(I.3.13), Hs и Vsi при Po. В соответствии с (I.3.12)-(I.3.13), Hs и  Hsi выражаются как Hsi выражаются как
|
Hs = Hso + Vso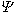 , ,
|
(I.3.16)
|
и
где 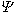 = 5/4 (Po + = 5/4 (Po + )1/5 [(P + )1/5 [(P +  )4/5 - (Po + )4/5 - (Po + )4/5]. )4/5].
Стандартизуя уравнение (I.3.11) относительно To и Po, и используя (I.3.16)-(I.3.17), получим
|
Gs=HToPo-TSToPo+Vso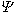 + c + c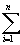 [RT ln(1-ei)- [RT ln(1-ei)- Hsio(1-T/To)eoi/(1-eoi)-RT ln(1-eoi)], Hsio(1-T/To)eoi/(1-eoi)-RT ln(1-eoi)],
|
(I.3.18)
|
где SToPo = -(дGs/дT)ToPo = Sso + 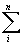 ci[ ci[ Hsio/To eoi/(1-eoi) - R ln(1-eoi)], Hsio/To eoi/(1-eoi) - R ln(1-eoi)],
HToPo = Hso + 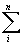 ci ci  Hsio eoi/(1-eoi), GToPo = HToPo - ToSToPo = Hso - ToSso + RTo Hsio eoi/(1-eoi), GToPo = HToPo - ToSToPo = Hso - ToSso + RTo 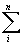 ci ln(1-eoi), ci ln(1-eoi),
и
ei = exp(- Hs/RT) и eoi = exp(- Hs/RT) и eoi = exp(- Hsio/RTo). Hsio/RTo).
GToPo, HToPo и SToPo - соответственно мольная энергия Гиббса, энтальпия и энтропия вещества при стандартных To и Po. Если To=0 K, то все члены уравнения, содержащие To равны нулю. Поскольку вибрационные спектры реальных веществ сложны, общее число параметров ci,  Hsio и Hsio и  Vsio в уравнении (I.3.18) должно быть большим. Поэтому, для петрологических целей можно использовать эмпирическую параметризацию уравнения (I.3.18) при n<5. В этом случае эмпирические величины ci, Vsio в уравнении (I.3.18) должно быть большим. Поэтому, для петрологических целей можно использовать эмпирическую параметризацию уравнения (I.3.18) при n<5. В этом случае эмпирические величины ci,  Hsio и Hsio и  Vsio можно рассматривать как обобщенные характеристики n групп осцилляторов, значительно различающихся по энергиям переходов. Очевидно, что уравнение (I.3.18) может быть прямо использовано для описания и расчета потенциала Гиббса и других термодинамических свойств однокомпонентных минералов, не демонстрирующих явлений разупорядочения при повышении температуры. Vsio можно рассматривать как обобщенные характеристики n групп осцилляторов, значительно различающихся по энергиям переходов. Очевидно, что уравнение (I.3.18) может быть прямо использовано для описания и расчета потенциала Гиббса и других термодинамических свойств однокомпонентных минералов, не демонстрирующих явлений разупорядочения при повышении температуры.
Конфигурационная часть потенциала Гиббса
Если с повышением температуры в конденсированном веществе протекают процессы разупорядочения, ведущие к 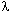 -переходу (включая изменение агрегатного состояния флюида) тогда уравнение (I.3.18) должно быть дополнено зависимостью от параметра порядка -переходу (включая изменение агрегатного состояния флюида) тогда уравнение (I.3.18) должно быть дополнено зависимостью от параметра порядка 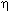 . Теоретические подходы к описанию переходов порядок-беспорядок хорошо развиты для кристаллических веществ (например, Ландау и Лифшиц, 1995; Пригожин и Дефэй, 1966; Feynman, 1972; Thompson, 1969) и по аналогии могут быть использованы для описания переходов жидкость-газ во флюидах. . Теоретические подходы к описанию переходов порядок-беспорядок хорошо развиты для кристаллических веществ (например, Ландау и Лифшиц, 1995; Пригожин и Дефэй, 1966; Feynman, 1972; Thompson, 1969) и по аналогии могут быть использованы для описания переходов жидкость-газ во флюидах.
В соответствии с концепцией внутрифазового равновесия (например, Thompson, 1969), процесс перехода порядок-беспорядок может рассматриваться как внутренняя реакция
|
aA + bB + ... + dD = 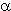 , ,
|
(I.3.19)
|
где A,B,...,D - разупорядоченные частицы, 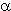 = AaBb...Dd - упорядоченная частица, a,b,..,d - стехиометрические коэффициенты. Схема реакции упорядочения (I.3.19) может быть различной и зависит от природы конкретного вещества. Выбор схемы упорядочения крайне важен, поскольку она заметно влияет на конфигурационную часть потенциала Гиббса. Условие термодинамического равновесия для реакции (I.3.19) имеет вид = AaBb...Dd - упорядоченная частица, a,b,..,d - стехиометрические коэффициенты. Схема реакции упорядочения (I.3.19) может быть различной и зависит от природы конкретного вещества. Выбор схемы упорядочения крайне важен, поскольку она заметно влияет на конфигурационную часть потенциала Гиббса. Условие термодинамического равновесия для реакции (I.3.19) имеет вид
|
 Gord = RTln(Kord) + Gord = RTln(Kord) +  Goord + Goord +  Geord = 0, Geord = 0,
|
(I.3.20)
|
где Kord = Xa/(XAa.XBb.....XDd) и XA+XB+..+XD+Xa = 1. XA, XB+..+XD - мольные доли (термодинамические вероятности) разупорядоченных частиц A,B,...,D, соответственно, Xa - мольная доля (термодинамическая вероятность) упорядоченной частицы a.  Goord и Goord и  Geord - изменение стандартной и избыточной энергии Гиббса в реакции (I.3.19), соответственно. Дополнительная энергия Гиббса относительно упорядоченного состояния (Xa = 1) будет Geord - изменение стандартной и избыточной энергии Гиббса в реакции (I.3.19), соответственно. Дополнительная энергия Гиббса относительно упорядоченного состояния (Xa = 1) будет
|
Ga = {RT[XAln(XA) + XBln(XB) +...+ XDln(XD) + Xaln(Xa)] -
 Goord(1 - Xa)/Z + Goord(1 - Xa)/Z +  Geord}/[1 + Xa(Z - 1)], Geord}/[1 + Xa(Z - 1)],
|
(I.3.21)
|
где нормировочный коэффициент Z=a+b+...+d, и Geord - интегральная избыточная энергия Гиббса смешения упорядоченных и разупорядоченных частиц.
В изобарно-изотермических условиях, равновесие в гомогенной фазе определяется условием минимума энергии Гиббса
|
Gs+a = Gs + caGa = min
|
(I.3.22)
|
где Gs+a - мольная энергия Гиббса вещества с 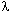 -переходом, ca - число степеней свободы, соответствующих реакции (I.3.19). Параметр порядка -переходом, ca - число степеней свободы, соответствующих реакции (I.3.19). Параметр порядка 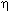 , в соответствии с принятым здесь формализмом равен Xa. Он количественно характеризует процесс упорядочения и стремится к максимуму (Xamax < 1) в упорядоченной фазе с понижением температуры, тогда как с повышением температуры он стремиться к минимуму (Xamin > 0) в разупорядоченной фазе. , в соответствии с принятым здесь формализмом равен Xa. Он количественно характеризует процесс упорядочения и стремится к максимуму (Xamax < 1) в упорядоченной фазе с понижением температуры, тогда как с повышением температуры он стремиться к минимуму (Xamin > 0) в разупорядоченной фазе.
Используя формализм Маргулеса для описания избыточной энергии Гиббса, Geord в уравнении (I.3.21) может быть записано как
|
Geord = 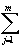 WGj(1 - Xa)(Xa) j, WGj(1 - Xa)(Xa) j,
|
(I.3.23)
|
где WGj- параметры Маргулеса. Число членов ряда m не лимитировано, однако известно, что случаи с m>2 для реальных веществ довольно редки (Chatterjee, 1991).
Если 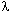 -переход ведет к заметному изменению тепловых колебаний атомов, это изменение необходимо учесть в описании энергетических эффектов осцилляторов. Следовательно, Gs в уравнении (I.3.22) будет также зависеть от Xa. Предположим, что с определенного энергетического уровня m, зависящего от Xa, энтальпийный эффект перехода -переход ведет к заметному изменению тепловых колебаний атомов, это изменение необходимо учесть в описании энергетических эффектов осцилляторов. Следовательно, Gs в уравнении (I.3.22) будет также зависеть от Xa. Предположим, что с определенного энергетического уровня m, зависящего от Xa, энтальпийный эффект перехода Hsi изменяется. Тогда, статистическая сумма Y0i в уравнении (I.3.7) вычисляется как Hsi изменяется. Тогда, статистическая сумма Y0i в уравнении (I.3.7) вычисляется как
где  Hi Hi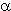 - энтальпийные эффекты энергетических переходов ( - энтальпийные эффекты энергетических переходов ( Hi0), начиная с нулевого уровня до уровня (m-1) в упорядоченной фазе, Hi0), начиная с нулевого уровня до уровня (m-1) в упорядоченной фазе,  Hi Hi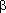 - энтальпийные эффекты энергетических переходов, начиная с уровня m в разупорядоченной фазе, - энтальпийные эффекты энергетических переходов, начиная с уровня m в разупорядоченной фазе,  Hi Hi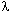 - энтальпийный эффект перехода с нулевого уровня на уровень m как функция Xa, представленная в виде степенного ряда: - энтальпийный эффект перехода с нулевого уровня на уровень m как функция Xa, представленная в виде степенного ряда:
где  Hi Hi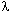 j - параметры разложения. Тогда, уравнение (I.3.18) принимает форму j - параметры разложения. Тогда, уравнение (I.3.18) принимает форму
где e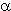 i=exp(- i=exp(- Hsi Hsi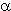 /RT), e /RT), e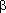 i=exp(- i=exp(- Hsi Hsi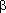 /RT), e /RT), e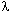 i=exp(- i=exp(- Hsi Hsi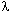 /RT), eoi=exp(- /RT), eoi=exp(- Hsi Hsi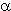 o/RTo), o/RTo),
 Hsi Hsi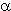 = = Hsi Hsi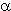 o + o +  Vsi Vsi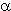 o o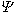 , ,  Hsi Hsi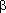 = = Hsi Hsi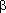 o + o +  Vsi Vsi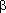 o o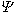 , and , and  Hsi Hsi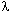 = = 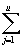 ( ( Hsi Hsi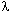 jo + jo +  Vsi Vsi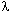 jo jo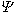 ) (Xa)j-1. ) (Xa)j-1.
 Hsi Hsi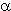 , ,  Hsi Hsi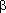 и и  Hsi Hsi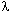 - величины - величины  Hia, Hia,  Hi Hi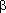 и и  Hi Hi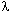 в расчете на NA осцилляторов. в расчете на NA осцилляторов.
Чтобы учесть особенности процессов упорядочения в различных агрегатных состояниях, формулировка потенциала Гиббса для минералов и флюидов будет рассмотрена ниже раздельно.
Уравнение для минералов.
Увеличение энтропии системы при разупорядочении кристаллических веществ главным образом связано с увеличением эффективного числа частиц и учтено введением нормировочного коэффициента Z в уравнении (I.3.21). Это позволяет предположить  Goord в уравнении (I.3.21) и WGj в уравнении (I.3.23) не зависящими от T. Кроме того, изменение объема системы в реакции (I.3.19) для кристаллических веществ является малым и может быть выражено в форме схожей с уравнением (I.3.14). Goord в уравнении (I.3.21) и WGj в уравнении (I.3.23) не зависящими от T. Кроме того, изменение объема системы в реакции (I.3.19) для кристаллических веществ является малым и может быть выражено в форме схожей с уравнением (I.3.14).
Тогда
и
|
WGj = WHj + WVj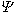 , ,
|
(I.3.28)
|
где  Hoord и Hoord и  Voord - соответственно, энтальпийный и объемный эффекты реакции упорядочения при 0 K и Po, WH и WV - соответственно, энтальпийный и объемный параметры Маргулеса при 0 K и Po. Voord - соответственно, энтальпийный и объемный эффекты реакции упорядочения при 0 K и Po, WH и WV - соответственно, энтальпийный и объемный параметры Маргулеса при 0 K и Po.
Используя уравнения (I.3.16)-(I.3.28), мольная энергия Гиббса минерала с 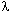 -переходом, стандартизованная на упорядоченную фазу (X -переходом, стандартизованная на упорядоченную фазу (X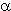 = 1) запишется как = 1) запишется как
где Gs задается либо уравнением (I.3.18) (когда изменения в тепловых колебаниях полагаются незначительными), либо уравнением (I.3.26) (когда изменения в тепловых колебаниях должны быть учтены).
Уравнение для флюидов.
В отличие от твердых веществ, переход жидкость-газ ведет к значительному увеличению объема системы и, следовательно, объемный эффект реакции (I.3.19) не может считаться малым. Кроме того, увеличение энтропии системы в этом переходе связано не только с увеличением эффективного числа частиц, но и с изменением поступательных и вращательных степеней свободы молекул. Это означает, что  Goord в уравнении (I.3.21) и WGj в уравнении (I.3.23) будет сильно зависеть как от температуры, так и от давления. Чтобы получить конкретные выражения для этих зависимостей необходимо проанализировать особенности процесса упорядочения во флюидном состоянии. Goord в уравнении (I.3.21) и WGj в уравнении (I.3.23) будет сильно зависеть как от температуры, так и от давления. Чтобы получить конкретные выражения для этих зависимостей необходимо проанализировать особенности процесса упорядочения во флюидном состоянии.
Любой однокомпонентный флюид существует в двух агрегатных состояниях (газ и жидкость), различающихся в степени ассоциированности (т.е., упорядоченности) молекул, ниже критической точки и становится гомогенным выше этой точки. Мы рассматриваем ассоциацию молекул флюида как специфический тип процесса упорядочения. Чтобы определить параметр упорядочения, предположим, что молекулы флюида могут существовать в двух состояниях ("жидкоподобном" и "газоподобном") при любых P и T, и что эти два состояния различаются энергиями взаимодействия молекул с окружением и, следовательно, мольными парциальными энергиями Гиббса. Переход из одного состояния в другое, связанный с процессом ассоциирования молекул, может быть выражен следующей реакцией упорядочения
где Gas - молекула в "газоподобном" (свободном, разупорядоченном) состоянии, Liq - молекула в "жидкоподобном" (ассоциированном, упорядоченном) состоянии. Далее мы будем называть эти молекулы газоподобными и жидкоподобными, соответственно. Вдоль линии кипения жидкости будут сосуществовать две равновесные фазы, различающиеся пропорциями (мольными долями, термодинамическими вероятностями) данных молекул (рис. I.5). В этом случае равновесие (I.3.30) будет иметь место как внутри каждой из фаз так и между ними. В отличие от минералов, мыполагаем, что стехиометрия реакции упорядочения (I.3.30) не зависит от природы перехода газ-жидкость и одинакова для всех флюидов. В соответствии с этим в уравнении (I.3.21) Z=1 для всех флюидов.
Для гомогенного флюида условие равновесия для реакции (I.3.30), в соответствии с уравнением (I.3.20) будет следующим
|
RTln(XLiq/XGas) +  Goord + Goord +  Geord = 0, Geord = 0,
|
](I.3.31)
|
где  Goord и Goord и  Geord - соответственно, изменение стандартной и избыточной мольной энергии Гиббса в реакции (I.3.30), XLiq и XGas - соответственно, мольные доли (термодинамические вероятности) жидкоподобных и газоподобных молекул (XGas=1-XLiq). В соответствии с уравнениями (I.3.21) и (I.3.22), интегральная мольная энергия Гиббса флюида (Gs+a), стандартизованная на жидкоподобное (упорядоченное) состояние запишется как Geord - соответственно, изменение стандартной и избыточной мольной энергии Гиббса в реакции (I.3.30), XLiq и XGas - соответственно, мольные доли (термодинамические вероятности) жидкоподобных и газоподобных молекул (XGas=1-XLiq). В соответствии с уравнениями (I.3.21) и (I.3.22), интегральная мольная энергия Гиббса флюида (Gs+a), стандартизованная на жидкоподобное (упорядоченное) состояние запишется как
|
Gs+a = Gs + RT[XGasln(XGas) + XLiqln(XLiq)] + Ge - XGas Goord = min, Goord = min,
|
(I.3.32)
|
где Gs - стандартная мольная энергия Гиббса конденсированного вещества, сложенного жидкоподобными молекулами, заданная уравнением (I.3.18) либо (I.3.26); Ge - избыточная мольная энергия смешения жидкоподобных и газоподобных молекул. Следовательно, в соответствии с нашей моделью параметр порядка определен как 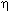 = X = X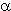 = XLiq. = XLiq.
Два последних члена в уравнении 32 могут быть записаны в виде
|
Ge - XGas Goord = GP + GT, Goord = GP + GT,
|
(I.3.33)
|
где GP = 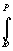 (- (- VoordXGas - Ve)dP, and GT = -XGas( VoordXGas - Ve)dP, and GT = -XGas( Hoord - T Hoord - T Soord)+He - TSe + Soord)+He - TSe +
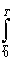 (- (- CPo(T)ordXGas + CPe(T))dT - T CPo(T)ordXGas + CPe(T))dT - T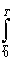 [(- [(- Cpoord(T)XGas + CPe(T))/T]dT. Cpoord(T)XGas + CPe(T))/T]dT.
 Voord и Ve - соответственно, стандартный объемный эффект реакции (I.3.30) и избыточный объем смешения как функции P и T; Voord и Ve - соответственно, стандартный объемный эффект реакции (I.3.30) и избыточный объем смешения как функции P и T;  Hoord и Hoord и  Soord- соответственно, стандартные энтальпийный и энтропийный эффекты реакции (I.3.30) при Po и To; He и Se - соответственно, вклады в избыточную энтальпию и энтропию, не связанные с Ve at Po and To; Soord- соответственно, стандартные энтальпийный и энтропийный эффекты реакции (I.3.30) при Po и To; He и Se - соответственно, вклады в избыточную энтальпию и энтропию, не связанные с Ve at Po and To;  Cpoord(T) и CPe(T) - соответственно, стандартный теплоемкостный эффект реакции (I.3.30) и избыточная теплоемкость как функции температуры при Po. Cpoord(T) и CPe(T) - соответственно, стандартный теплоемкостный эффект реакции (I.3.30) и избыточная теплоемкость как функции температуры при Po.
Для определения вида GP в уравнении (I.3.33), предположим, что объем фазы состоящей только из газоподобных молекул может быть представлен в виде суммы собственного объема молекул Vs и свободного объема Vf (Пригожин и Дефэй, 1966). Тогда
|
VoGas = Vs + Vf = Vs + RT/P.
|
(I.3.34)
|
Объем моля вещества состоящего из жидкоподобных молекул положим равным собственному объему молекул
Тогда, стандартный объемный эффект реакции (I.3.30)
 Voord = VoLiq- VoGas = -RT/P. Voord = VoLiq- VoGas = -RT/P.
С учетом уравнений (I.3.34) и (I.3.35) общий объем V вещества, состоящего из жидкоподобных и газоподобных молекул будет
|
V = XGasVoGas + XLiqVoLiq - Ve = Vs - XGas Voord - Ve = Vs + XGasRT/P - Ve. Voord - Ve = Vs + XGasRT/P - Ve.
|
(I.3.36)
|
Отрицательный избыточный объем (-Ve) соответствует уменьшению свободного объема Vf, обусловленному притяжением между любыми молекулами. Тогда, с учетом уравнения Ван-Дер-Ваальса можно записать
P = RT/(V - 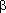 ) - ) -  a, a,
где 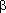 - поправка на собственный объем молекул (т.е., - поправка на собственный объем молекул (т.е., 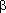 = Vs) и = Vs) и  a = const/V2 - поправка на притяжение между молекулами. Отсюда, уравнение (I.3.36) может быть переписано в виде a = const/V2 - поправка на притяжение между молекулами. Отсюда, уравнение (I.3.36) может быть переписано в виде
|
V = Vs + XGasRT/P - Ve = Vs + XGasRT/P/(P +  a). a).
|
(I.3.37)
|
Очевидно, сто  a зависит от среднего расстояния между молекулами во флюиде. Учитывая объемный эффект реакции (I.3.30), это расстояние будет функцией XLiq. При снижении внешнего давления объем системы стремится к объему идеального газа (RT/P) а XLiq и a зависит от среднего расстояния между молекулами во флюиде. Учитывая объемный эффект реакции (I.3.30), это расстояние будет функцией XLiq. При снижении внешнего давления объем системы стремится к объему идеального газа (RT/P) а XLiq и  a стремятся к нулю. При увеличении давления XLiq и fa также повышаются. Следовательно, a стремятся к нулю. При увеличении давления XLiq и fa также повышаются. Следовательно,  a может быть представлена как функция XLiq в виде ряда a может быть представлена как функция XLiq в виде ряда
где a1 , a1 , a2 , ..., и a2 , ..., и  an - коэффициенты, не зависящие от XLiq. Очевидно, при стремлении XLiq к 1, an - коэффициенты, не зависящие от XLiq. Очевидно, при стремлении XLiq к 1,  a должно стремиться к a должно стремиться к  [см. уравнение (I.3.14)], поскольку обе поправки характеризуют те же самые силы притяжения между молекулами. Тогда в соответствии с уравнением (I.3.38) можно записать [см. уравнение (I.3.14)], поскольку обе поправки характеризуют те же самые силы притяжения между молекулами. Тогда в соответствии с уравнением (I.3.38) можно записать
Для перехода из жидкоподобного состояния в газоподобное, когда расстояния между молекулами значительно увеличиваются, уравнения (I.3.37)-(I.3.38) обеспечивают дополнительную коррекцию на изменение эффективных сил притяжения между молекулами. Принимая  a=0 за стандартное условие для газоподобных молекул при интегрировании уравнения (I.3.36) в соответствии с (I.3.34), получим следующее выражение для GP a=0 за стандартное условие для газоподобных молекул при интегрировании уравнения (I.3.36) в соответствии с (I.3.34), получим следующее выражение для GP
|
GP = XGasRTln[(P + a)/Po] a)/Po]
|
(I.3.40)
|
Используя ряд Маргулеса (23) для выражения интегральной избыточной энергии Гиббса смешения жидкоподобных и газоподобных молекул во флюиде и полагая  Cpoord(T) и CPe(T) постоянными, GT в уравнении (I.3.33) может быть определено как Cpoord(T) и CPe(T) постоянными, GT в уравнении (I.3.33) может быть определено как
где WGj = WHj - TWSj + WCpj[T-To-Tln(T/To)]. Cpoord - стандартный теплоемкостный эффект реакции (I.3.30) при Po и To, W - параметры Маргулеса.
С использованием уравнений (I.3.32)-(I.3.41) мольная энергия Гиббса флюида, стандартизованная относительно упорядоченного состояния (X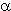 = XLiq = 1) будет = XLiq = 1) будет
где Gs задается уравнением (I.3.18), когда изменения тепловых колебаний включены в конфигурационную часть потенциала Гиббса, либо уравнением (I.3.26), когда эти изменения рассматриваются отдельно. Хорошо видно, что форма уравнения (I.3.42) очень похожа на уравнение (I.3.29), выведенное для минералов. Это сходство прямо следует из использованной термодинамической аналогии описания процессов упорядочения в кристаллических веществах и флюидах.
Тестирование уравнений
Расчетная процедура
При тестировании уравнений ставилась задача описания термодинамических свойств веществ в экспериментально изученном интервале Р-Т параметров с точностью близкой к экспериментальной и достаточной для использования уравнений состояния во взаимосогласованной базе термодинамических данных по фазовым равновесиям. Для потенциала Гиббса она соответствует среднеквадратичной погрешности описания <+20.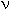 кал/моль (где кал/моль (где 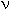 - число атомов в молекуле вещества). В качестве стандартных были приняты To=298.15 K и Po=1 бар. - число атомов в молекуле вещества). В качестве стандартных были приняты To=298.15 K и Po=1 бар.
Выведенные уравнения были протестированы на основе экспериментальных данных для системы CaO-FeO-MgO-Al2O3-SiO2-Na2O-K2O и табулированных термодинамических свойств однокомпонентных газов. Для расчета взаимосогласованных термодинамических параметров уравнений на основе данных по термофизическим свойствам веществ и фазовым переходам была создана авторская программа, базирующаяся на нелинейном методе наименьших квадратов. При этом использовались циклическая итерационная расчетная процедура и нормализация ошибки описания измеренных параметров на экспериментальные погрешности. Нелинейная внутренняя процедура была также использована для минимизации потенциала Гиббса и расчета равновесных значения параметра упорядочения при заданных Р и Т. Для расчета термодинамических свойств (H, S, V, Cp и т.д.) веществ на основе уравнения для потенциала Гиббса использовались известные термодинамические соотношения в сочетании с численным дифференцированием. В качестве стандартных были приняты To=298.15 K и Po=1 бар.
Более детальное изложение метода взаимосогласования и подробная характеристика качества описания различных групп экспериментальных данных приведены в специальных статьях (Gerya & Perchuk, 1997a; Gerya et al., 1998).
Тестирование уравнений для минералов
Анализ применимости выведенных уравнений для кристаллических веществ был проведен для системы CaO-FeO-MgO-Al2O3-SiO2-Na2O-K2O. Тестирование показало, что для T>To требуемая точность описания достигается при n=2,  Vi = Vi = Vso в (I.3.18). Таким образом, уравнения состояния для упорядоченных кристаллических веществ содержат не более 9 уточняемых параметров. Vso в (I.3.18). Таким образом, уравнения состояния для упорядоченных кристаллических веществ содержат не более 9 уточняемых параметров.
Запишем окончательную форму уравнения для расчета потенциала Гиббса кристаллических веществ принятую в базе данных "ГеоПас"
|
Gs=HToPo-TSToPo+Vso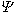 + +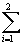 ci[RT ln(1-ei)- ci[RT ln(1-ei)- Hsio(1-T/To)eoi/(1-eoi)-RT ln(1-eoi)], Hsio(1-T/To)eoi/(1-eoi)-RT ln(1-eoi)],
|
(I.3.43)
|
где
ei = exp[-( Hsio+ Hsio+ Vso Vso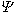 )/RT], eoi = exp(- )/RT], eoi = exp(- Hsio/RTo), Hsio/RTo),
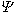 =5/4(Po+ =5/4(Po+ )1/5[(P+ )1/5[(P+ )4/5-(Po+ )4/5-(Po+ )4/5]. )4/5].
Расчетные значения параметров уравнения (I.3.43) для индивидуальных веществ системы CaO-FeO-MgO-Al2O3-SiO2-Na2O-K2O приведены в таблице I.4. Для некоторых веществ (например, Fa) характерен низкотемпературный 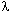 -переход, который не влияет на минеральные равновесия при T>To и учитен в интегральной форме в параметрах HToPo и SToPo. Высокотемпературный -переход, который не влияет на минеральные равновесия при T>To и учитен в интегральной форме в параметрах HToPo и SToPo. Высокотемпературный 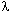 -переход характерен только для кварца, поэтому для описания его термодинамических свойств использовано уравнение (I.3.29) -переход характерен только для кварца, поэтому для описания его термодинамических свойств использовано уравнение (I.3.29)
Термодинамические свойства кварца наилучшим образом описываются с учетом реакции упорядочения (I.3.19) вида
|
3SiO2(Qtz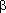 ) = Si3O6(Qtz ) = Si3O6(Qtz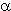 ). ).
|
(I.3.44)
|
(Castex, Madon, 1995; Spearing et al., 1992). Поскольку тепловые колебания атомов в 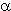 -кварце значительно отличаются от таковых в -кварце значительно отличаются от таковых в 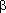 -кварце (например, Ghose, 1985), то уравнение (I.3.26) было использовано для Gs в уравнении (I.3.29). С учетом n=2, u=2 в уравнении (I.3.26) и m=1, c -кварце (например, Ghose, 1985), то уравнение (I.3.26) было использовано для Gs в уравнении (I.3.29). С учетом n=2, u=2 в уравнении (I.3.26) и m=1, c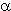 =1 в уравнении (I.3.29) уравнение для потенциала Гиббса кварца имеет вид =1 в уравнении (I.3.29) уравнение для потенциала Гиббса кварца имеет вид
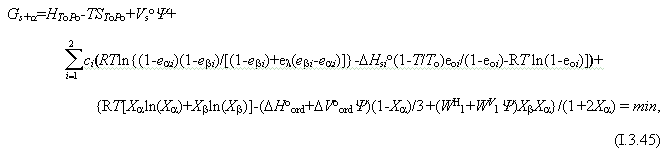
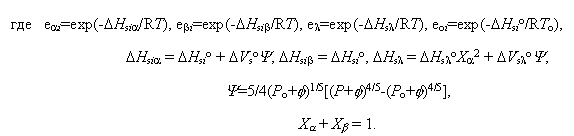
X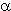 и X и X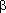 - мольные доли упорядоченного и разупорядоченного кварца, соответственно. Уравнение (I.3.45) учитывает значительное снижение коэффициента термического расширения b-кварца по сравнению с a-кварцем. По сравнению с (I.3.43) уравнение (I.3.45) содержит шесть дополнительных уточняемых параметров, связанных с существованием в кварце - мольные доли упорядоченного и разупорядоченного кварца, соответственно. Уравнение (I.3.45) учитывает значительное снижение коэффициента термического расширения b-кварца по сравнению с a-кварцем. По сравнению с (I.3.43) уравнение (I.3.45) содержит шесть дополнительных уточняемых параметров, связанных с существованием в кварце 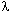 -перехода. Расчетные значения параметров уравнения (I.3.45) для кварца приведены в таблице I.4. -перехода. Расчетные значения параметров уравнения (I.3.45) для кварца приведены в таблице I.4.
Тестирование уравнений для флюидов
Уравнение состояния для флюидов было протестировано на основе табличных данных по термодинамическим свойствам H2O, CO2, CH4 и Ar. Полагая, что изменение тепловых колебаний учтено в конфигурационной части потенциала Гиббса, для описания Gs в уравнении (I.3.42) мы воспользовались формулой (I.3.18).
Требуемая точность описания была достигнута при n=2 в уравнении (I.3.18) и m=1, q=2 в уравнении (I.3.42). Соответствующее уравнение потенциала Гиббса флюидов имеет вид
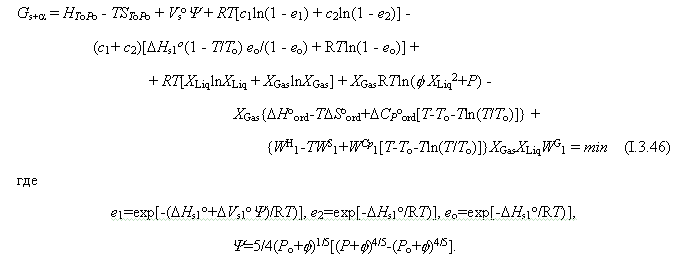
Расчетные значения параметров уравнения (I.3.46) для H2O, CO2, CH4 и Ar приведены в таблице I.5. Для вычисления RTlnf любого из газов при заданных Р и Т можно воспользоваться формулой
|
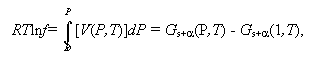
|
(I.3.47)
|
где Gs+a(P,T) и Gs+a(1,T) - равновесные значения Gs+a = min в (I.3.46) при заданной температуре Т и давлениях Р и 1 бар, соответственно.
Обсуждение выведенных уравнений.
Главное свойство выведенных уравнений для потенциала Гиббса веществ, где имеют место явления разупорядочения, состоит в необходимости расчета равновесного значения параметра порядка. Графический вариант такой процедуры для равновесия (I.3.30) в жидкости, в точке фазового превращения и в газе показан на рис.I.6. При температуре 250oС минимуму энергии Гиббса, Ga соответствует мольная доля жидкой воды 0.68, а в точке двухфазного равновесия при 300oС имеется два равноправных минимума энергии Гиббса, Ga = -890 кал/моль. В каждой из сосуществующих фаз мольная доля жидкоподобных молекул различна: в жидкой фазе XLiq = 0.62, а в равновесной с ней газовой фазе XLiq = 0.05. В поле газовой фазы, отвечающей минимуму энергии Гиббса при температуре 350оС фазы, XLiq почти такое же, 0.04. Такая процедура позволяет посредством минимизации энергии Гиббса вычислять равновесные значения XLiq при заданных Р-Т параметрах.
На рис. I.7 показано расчетное изменение параметров упорядочения для кварца (рис. I.7а) и водного флюида (рис. I.7б) с температурой при различных давлениях (в том числе вдоль линий фазовых переходов Qtz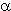 -Qtz -Qtz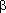 и H2OLiq-H2Ogas). Видно, что вдоль линий фазовых переходов и H2OLiq-H2Ogas). Видно, что вдоль линий фазовых переходов
сосуществуют две равновесные фазы, различающиеся между собой соотношением упорядоченных и разупорядоченных частиц. Равновесие (I.3.30) при этом устанавливается как между фазами, так и внутри каждой из них. Видно также, что область распада для кварца расширяется с давлением (гипотетическая критическая точка соответствует T = 553oC, P = -0.88 kbar). Ниже этой точки по давлению может существовать гипотетическая гомогенная фаза кремнезема, параметр Xa в которой будет меняться постепенно по мере повышения температуры (рис. I.7а). Аналогичные соотношения характерны для гомогенного водного флюида, существующего выше критической точки (рис. I.7б). Хорошо видно, что в области существования гомогенной фазы переход между упорядоченным и разупорядоченным состояниями совершается постепенно. В этой области изобарные теплоемкости вещества имеют плавный максимум в области максимального изменения параметра упорядочения и, следовательно, структурного состояния вещества с температурой (рис. I.8). Рисунок I.9 показывает особенности изменения объемов кварца (рис. I.9а) и воды (рис. I.9б) с повышением температуры в связи с явлениями разупорядочения. В целом рисунки 1.7-1.9 демонстрируют явное термодинамическое сходство явлений упорядочения в кристаллическом и флюидном состояниях, подтверждая корректность избранного подхода.
Важный вопрос касается физического смысла параметра порядка X. Как для флюидов так и для кварца этот параметр не может быть напрямую определен из каких либо физических измерений и выглядит абсолютно абстрактным. Однако для флюидов можно установить связь параметра порядка с числом молекулярных кластеров, возникающих при ассоциировании молекул (Барелко и др., 1994). Можно показать, что уравнения (I.3.42) и (I.3.46) справедливы и при рассмотрении процесса ассоциирования молекул флюида в форме реакции кластеризации (Барелко и др., 1994)
A + An = An+1,
где A -мономер, An и An+1 - кластеры размерности n и n+1, соответственно. Соответствующую константу реакции полагаем не зависящей от n. В этом случае XGas может быть интерпретировано как мольная доля мономеров а XLiq - как суммарная мольная доля кластеров размерностью n > 2. Концепция существования двух различных состояний молекул гомогенного флюида согласуется с исследованиями структуры воды (Gorbaty & Demianets, 1983) показавшими, что близкритические флуктуации сохраняются и при повышенных P-T параметрах (выше критической точки до давления 1 кбар и температуры 500oC). Таким образом, в надкритической области в гомогенном флюиде существуют жидкоподобные и газоподобные пространственные флуктуации.
Другие примеры соответствия между параметром порядка и физическими измерениями показаны на рис.I.10. Диаграмма I.10а показывает отрицательную линейную корреляцию расчетных значений параметра Xa с суммой среднеквадратичных отклонений (MSD) атомов кислорода в структуре кварца, определенных для области 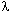 - перехода (Kihara, 1990). Высокий коэффициент корреляции (r = 0.9868) показывает, что расчетное уменьшение Xa с повышением температуры отражает реальный физический механизм разупорядочения. На рисунке I.10б мольная жидкоподобных молекул XLiq сопоставлена с мольной долей водородных связей XH (Gorbaty & Kalinichev, 1995), рассчитанной по данным физических измерений (хорошо известно, что ассоциирование молекул в водном флюиде определяется в основном водородными связями). Рисунок I.10в представляет сравнение XLiq с мольным процентом мономеров NM (Luck 1980). Высокие коэффициенты корреляции XLiq с XH (r = 0.942) и NM (r = 0.997) показывают, что XLiq количественно характеризует степень ассоциированности молекул водного флюида. Таким образом, можно заключить, что наш довольно абстрактный параметр порядка отражает физические процессы, протекающие как в минералах, так и во флюидах. - перехода (Kihara, 1990). Высокий коэффициент корреляции (r = 0.9868) показывает, что расчетное уменьшение Xa с повышением температуры отражает реальный физический механизм разупорядочения. На рисунке I.10б мольная жидкоподобных молекул XLiq сопоставлена с мольной долей водородных связей XH (Gorbaty & Kalinichev, 1995), рассчитанной по данным физических измерений (хорошо известно, что ассоциирование молекул в водном флюиде определяется в основном водородными связями). Рисунок I.10в представляет сравнение XLiq с мольным процентом мономеров NM (Luck 1980). Высокие коэффициенты корреляции XLiq с XH (r = 0.942) и NM (r = 0.997) показывают, что XLiq количественно характеризует степень ассоциированности молекул водного флюида. Таким образом, можно заключить, что наш довольно абстрактный параметр порядка отражает физические процессы, протекающие как в минералах, так и во флюидах.
Необходимо отметить, что предложенные уравнения содержат небольшое число (14-15) уточняемых параметров при описании таких сложных в термодинамическом отношении фаз как кварц и флюиды. Для сравнения, уравнения потенциала Гельмгольца, позволяющие описывать термодинамические свойства флюидов с достаточно высокой точностью в широком интервале Р-Т параметров обычно содержат 30-80 эмпирических коэффициентов (например, Stewart & Jacobson, 1989; Сычев и др., 1979; Алтунин, 1975; Saul & Wagner, 1989; Hill, 1990). Уравнение потенциала Гиббса для кварца (Dorogokupets, 1995), позволяющее корректно описывать его термодинамические свойства в области l-перехода содержит 26 параметров. В случае простых фаз уравнение (I.3.43) с 9 уточняемыми параметрами позволяет корректно описывать термодинамические свойства веществ в широком интервале P-T параметров. Тестирование на независимых данных (Gerya & Perchuk, 1997a; Gerya et al., 1998) показало, что выведенные уравнения для минералов и флюидов демонстрируют хорошие экстраполяционные свойства как по температуре, так и по давлению. Последнее обстоятельство особенно важно с учетом необходимости расчетов изменения плотностных свойств пород и минералов в области повышенных Р-Т параметров при численном геодинамическом моделировании.
Можно заключить, что полученные уравнения позволяют корректно описывать и экстраполировать термодинамические свойства кристаллических веществ и флюидов в широком интервале температур и давлений, что в полной мере соответствует целям создания базы термодинамических данных "ГеоПас".
| Полные данные о работе |
Геологический факультет МГУ |
|


