1.1.1. Элементы симметрии кристаллов
Изучение кристаллов начинается с рассмотрения их внешней формы. Внешняя форма хорошо сформированных кристаллических многогранников может быть описана с помощью элементов симметрии.
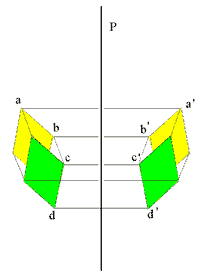 |
| Рис. 2. Отражение элементов кристалла в плоскости симметрии. |
Симметричным считается объект, который может быть совмещен сам с собой определенными преобразованиями: поворотами или (и) отражениями в зеркальной плоскости.
Элементы симметрии - это вспомогательные геометрические образы (плоскости, прямые линии, точки), с помощью которых обнаруживается симметрия фигур.
Рассмотрим элементы симметрии.
Плоскость симметрии - это воображаемая плоскость, которая делит фигуру на две равные части так, что одна из частей является зеркальным отражением другой. Плоскость симметрии обозначается буквой Р (рис.2). Если плоскостей симметрии в данном кристалле несколько, то перед обозначением плоскости ставится их число. Например 3Р ( три плоскости симметрии имеет спичечная коробка)(рис.4). В кристаллах может быть одна, две, три, четыре, пять, шесть, семь и девять плоскостей симметрии. Теоретически можно доказать, что восьми и более девяти плоскостей симметрии в кристаллах быть не может Многие кристаллы вообще не имеют ни одной плоскости симметрии.
Ось симметрии - воображаемая прямая линия , при повороте вокруг которой всегда на один и тот же угол происходит совмещение равных частей фигуры. Наименьший угол поворота вокруг оси, приводящий к такому совмещению, называется элементарным углом поворота оси симметрии a. Его величина определяет порядок оси симметрии n, который равен числу самосовмещений при полном повороте фигуры на 360o (n = 360/a).
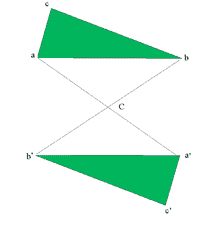 |
| Рис. 3. Отражение элементов кристалла в центре симметрии. |
Оси симметрии обозначаются буквой L с цифровым индексом, указывающим на порядок оси - Ln. Доказано, что в кристаллах возможны только оси второго, третьего, четвертого и шестого порядков.
Они обозначаются L2, L3 , L4 , L6. Осей пятого и порядка выше шестого в кристаллах не бывает. Оси третьего L3, четвертого L4 и шестого L6 порядка принято считать осями высшего порядка.
Центр симметрии (центр инверсии) - это такая точка внутри фигуры при проведении через которую любая прямая встретит на равном от нее расстоянии одинаковые и обратно расположенные части фигуры. Центр симметрии обозначается буквой С (рис.3). Если каждая грань кристалла имеет себе равную и параллельную или обратно параллельную, то данный кристалл обладает центром симметрии. Некоторые кристаллы могут не иметь центра симметрии (рис.5).
Перечень всех элементов симметрии кристалла, записанный в виде их символов, называется формулой симметрии или видом симметрии.
Cтрогий математический анализ (Гессель, 1830, Гадолин, 1867) показал, что существует всего 32 вида симметрии. Это все возможные для кристаллов комбинации элементов симметрии.
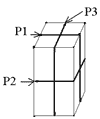 |
| Рис. 4. Три плоскости симметрии в одном кристалле |
32 вида симметрии объединяются в сингонии. Всего различают семь сингоний.
Название "сингония" происходит от греческого " син" - "сходно" и "гон" -"угол". Сингонию кристалла определяют по обязательным и сходным для каждой сингонии элементам симметрии, а также, основываясь на наличии или отсутсвии единичных направлений.
Единичное направление (Е) - это единственное, неповторяющееся какими-либо операциями симметрии данной группы направление в кристаллическом многограннике.
7 сингоний объединены в три категории.
- Низшая категория объединяет триклинную ,моноклинную и ромбическую сингонии. Кристаллы этих сингоний не имеют осей симметрии выше второго порядка.
- Средняя категория объединяет тригональную, тетрагональную и гексагональную сингонии. Кристаллы этих сингоний имеют только одну ось симметрии высшего порядка (L3, L4, L6), которые совпадают с единственным единичным направлением.
- Высшая категория - кубическая сингония - объединяет кристаллы, которые обязательно имеют 4L3. Единичных направлений нет. Все направления симметрично-равные.
Таблица 1. Названия и формулы 32 видов симметрии.
Оглавление| Назад| Следующая страница
Геологический факультет МГУ
 |
III Всероссийская научная школа "Математические исследования в кристаллографии, минералогии и петрографии" |
|
 |
Завершилась III Всероссийская научная школа "Математические исследования в кристаллографии, минералогии и петрографии" |
|
 |
Четвериков Сергей Дмитриевич |
|
 |
Фазовые отношения во фторсодержащей гранитной и нефелин-сиенитовой системах и распределение элементов между фазами: ЛИТЕРАТУРА |
|
|
|
|
|
|


