|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IX.6.2. Вывод шубниковских групп симметрии класса С2v
Проиллюстрируем принцип вывода шубниковских групп симметрии на примере групп, подчиненных точечной группе mm2 (С2v).
1. Выпишем 10 примитивных классических (полярных) федоровских групп симметрии: Pmm2, Pnn2, Pcc2, Pba2, Pmn21 , Pmc21 , Pma2, Pnc2, Pna21 , Pca21 (табл. 7).
2. Добавив к каждой из них операцию антитождества (1' ), получим 10 нейтральных (серых) групп антисимметрии: Pmm2 .1', Pmn21 . 1', .... и т.д.
3. Рассмотрим группы ромбической сингонии с цветными Р-решетками: P's = P'a = P'b = P'c , P'A = P'B = P'C , P'I . Поскольку в группах класса С2v горизонтальные и вертикальные направления топологически различны, то цветная центрировка вертикальных ребер или граней элементарной ячейки отличается от центрировки горизонтальных: P'a= P'b  P'c , P'A = P'B P'c , P'A = P'B  P'C . Легко выписать по 10 соответствующих шубниковских групп антисимметрии с решетками Р'c , P'C и P'I , в которых цветные трансляции одинаково расположены по отношению к исходным плоскостям 1-й и 2-й позиций символа ( табл. 7). P'C . Легко выписать по 10 соответствующих шубниковских групп антисимметрии с решетками Р'c , P'C и P'I , в которых цветные трансляции одинаково расположены по отношению к исходным плоскостям 1-й и 2-й позиций символа ( табл. 7).
Не следует забывать, однако, что присутствие дополнительных цветных векторов (в данном случае 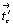 , , 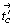 , , 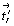 ) автоматически приводит к возникновению новых цветных элементов симметрии. В группах с решеткой Р'с возникшие цветные элементы симметрии совпадают (оказываются тождественно равными) с исходными классическими: mx. ) автоматически приводит к возникновению новых цветных элементов симметрии. В группах с решеткой Р'с возникшие цветные элементы симметрии совпадают (оказываются тождественно равными) с исходными классическими: mx. 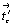 --> c'x , т.е. m --> c'x , т.е. m  c', так же как n c', так же как n  b'(a'), c b'(a'), c  m', b m', b  n', a n', a  n'. В группах с решетками P'C и P'I цветная трансляция n'. В группах с решетками P'C и P'I цветная трансляция 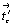 , косо расположенная к исходным элементам симметрии, обусловливает их чередование с элементами антисимметрии, что видно из развернутых записей групп: P'C nc2 = P'C n(c')c(n')2(2') и P'I ma2 = P'I m(n')a(c')2(2') (см. цветную вставку, рис. 164). , косо расположенная к исходным элементам симметрии, обусловливает их чередование с элементами антисимметрии, что видно из развернутых записей групп: P'C nc2 = P'C n(c')c(n')2(2') и P'I ma2 = P'I m(n')a(c')2(2') (см. цветную вставку, рис. 164).
При выводе Р-групп с цветной центрировкой горизонтальных ребер (a или b) или вертикальных граней (А или В) следует рассмотреть два варианта.
1-й вариант. Если плоскости 1-й и 2-й позиций символа одинаковы, т.е. без скольжения или с одинаковым скольжением (P'amm2, P'acc2, P'ann2, P'aba2), то безразлично в какой из них лежит центрирующий цветной вектор 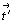 , т.е. P'a = P'b (рис. 165, а). Однако при этом сами плоскости становятся топологически различными по отношению к вектору , т.е. P'a = P'b (рис. 165, а). Однако при этом сами плоскости становятся топологически различными по отношению к вектору 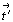 (вектор (вектор 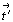 лежит в одной плоскости, но перпендикулярен другой). Цветная трансляция, параллельная исходным плоскостям классической симметрии, обусловливает их тождественность с возникающими плоскостями антисимметрии: m лежит в одной плоскости, но перпендикулярен другой). Цветная трансляция, параллельная исходным плоскостям классической симметрии, обусловливает их тождественность с возникающими плоскостями антисимметрии: m  b', n b', n  c', b(a) c', b(a)  m', c m', c  n', тогда как перпендикулярная - их чередование: m(m'), n(n'), c(c'), b(b'). В развернутом виде символы данных групп будут следующими: n', тогда как перпендикулярная - их чередование: m(m'), n(n'), c(c'), b(b'). В развернутом виде символы данных групп будут следующими:
P'amm2 (= P'bmm2) = P'am(m') m  a' 2(2'), a' 2(2'),
P'ann2 (= P'bnn2) = P'an(n') n  c' 2(2'), c' 2(2'),
P'acc2 (= P'bcc2) = P'ac(c') c  n' 2(2'), n' 2(2'),
P'aba2 (= P'bba2) = P'ab(b') a  m' 2(2') (см. рис. 164). m' 2(2') (см. рис. 164).
2-й вариант. Если плоскости 1-й и 2-й позиций символа разные, то небезразлично, вдоль какого из ребер элементарной ячейки направлена цветная трансляция 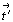 , т.е. в данном случае P'a , т.е. в данном случае P'a  P'b (см. рис. 165, б), ибо P'b (см. рис. 165, б), ибо 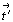 параллельна одной плоскости и перпендикулярна другой. В результате двух вариантов <Щзацвечивания> решеток появятся два типа групп антисимметрии. Например, P'amc21 (= P'bcm21) параллельна одной плоскости и перпендикулярна другой. В результате двух вариантов <Щзацвечивания> решеток появятся два типа групп антисимметрии. Например, P'amc21 (= P'bcm21)  P'bmc21 (= P'acm21) (см. рис. 164). Всего групп антисимметрии с центрированным ребром (групп P's) окажется 26: 10 с цветной решеткой Pc' и 16 с решеткой P'a (P'b). P'bmc21 (= P'acm21) (см. рис. 164). Всего групп антисимметрии с центрированным ребром (групп P's) окажется 26: 10 с цветной решеткой Pc' и 16 с решеткой P'a (P'b).
Аналогичные рассуждения приведут к 10 группам с цветной базоцентрированной ячейкой P'C и к 16 (4+6 . 2) бокоцентрированным группам с решеткой P'A , для которых небезразлично, какой из граней ячейки параллельна центрирующая трансляция 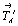 : :
4 - P'A mm2, P'A nn2, P'A cc2, P'A ba2,
12 - P'A mn21 (=P'Bnm21), P'A mc21 (=P'Bcm21), .... и т.д.,
P'A nm21 (=P'B mn21), P'A cm21(= P'B mc21) (см. табл. 7).
Не следует забывать и о результатах взаимодействий цветной трансляции 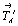 с порождающими элементами симметрии, т.е. о существовании в этих группах тождественно равных исходным или чередующихся с ними элементах антисимметрии (см. цветную вставку, рис. 166). с порождающими элементами симметрии, т.е. о существовании в этих группах тождественно равных исходным или чередующихся с ними элементах антисимметрии (см. цветную вставку, рис. 166).
Для того чтобы вывести группы антисимметрии ромбической гемиэдрии с классической P-решеткой, необходимо рассмотреть возможности <Щзацвечивания> подрешеточных элементов симметрии. При этом каждой из четырех групп с одинаковыми порождающими плоскостями симметрии (см. табл. 7) будут соответствовать 2 группы: с одной или двумя плоскостями антисимметрии, например Pb'a2'(=Pba' 2') и Pb'a' 2 (рис. 166), а каждой из оставшихся шести групп с различными порождающими элементами симметрии (см. табл. 7) - по 3 группы антисимметрии, например Pna21 --> Pn'a21', Pna' 21', Pn'a' 21 (см. цветную вставку, рис. 167).
В результате проведенного <Щзацвечивания> получили 26 групп антисимметрии с P-решеткой, изоморфных точечной группе Рmm2, т.е. всего 108 шубниковских групп: 10 классических (полярных), 10 нейтральных (серых), 62 группы с цветной решеткой, 26 с простой решеткой, но с цветными элементами симметрии.
Переходя к семейству групп с решетками C, A и B, следует иметь в виду, что если для групп классов D2 и D2h безразлично, какая пара граней зацентрирована, то для групп класса C2v различают базо- (C) и бокоцентрированные (A,B) решетки, обслуживающие 7 федоровских групп: Cmm2, Cmc21 , Ccc2 и Amm2, Ama2, Abm2, Aba2 (табл. 8). Добавив операцию антитождества (1'), соответственно получим 7 нейтральных (серых) групп антисимметрии: Cmm2 . 1', Cmc21 . 1',... и т.д.(табл. 8).
Перечислив все решетки с цветной центрировкой для базоцентрированной ячейки - C'a,b , C'c,I , C'A,B , следует обратить внимание на то, что цветная центрировка одного типа приводит за счет взаимодействия с классическим вектором 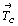 к автоматической центрировке другого типа. Отсюда для групп класса C2v каждая из перечисленных цветных решеток будет обслуживать лишь по 3 группы антисимметрии (табл. 8): к автоматической центрировке другого типа. Отсюда для групп класса C2v каждая из перечисленных цветных решеток будет обслуживать лишь по 3 группы антисимметрии (табл. 8):
С'c,I mm2, C'c,I mc21(= C'c,I cm21), C'c,I cc2;
C'a,bmm2, C'a,bmc21 (= C'a,bmc21), C'a,bcc2;
C'A,B mm2, C'A,B mc21 (= C'A,B cm21), C'A,B cc2.
В каждой из перечисленных групп с цветной решеткой C' в результате взаимодействия цветной трансляции с классическими элементами симметрии возникнут элементы антисимметрии. Например: C'a,b mc21 = C'a,b m  b' (b b' (b  m')c m')c  n'(n n'(n  c' ) 21 (21' ) (см. цветную вставку, рис. 168). c' ) 21 (21' ) (см. цветную вставку, рис. 168).
Каждая из бокоцентрированных решеток - A'b,c , A'a,I и A'B,C - даст по 4 группы антисимметрии (табл. 8). Например (рис. 168):
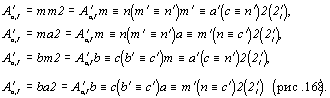
Трем федоровским группам с I-решеткой - Imm2, Ima2 и Iba2 - соответствуют 3 нейтральные группы.
Поскольку цветная центрировка какого-либо ребра влечет за собой центрировку перпендикулярной этому ребру грани (вектор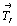 ), то нет необходимости отдельно рассматривать центрировку граней ячейки. Три возможных варианта - I'b,B , I'a,A и I'c,C - реализуются лишь в двух семействах гемиморфных групп антисимметрии, подчиненных классу C2v: ), то нет необходимости отдельно рассматривать центрировку граней ячейки. Три возможных варианта - I'b,B , I'a,A и I'c,C - реализуются лишь в двух семействах гемиморфных групп антисимметрии, подчиненных классу C2v:
I семейство - I'c,C mm2, I'c,C ma2(=I'c,C bm2), I'c,C ba2;
II семейство - I'a,A mm2, I'a,Ama2, I'a,A bm2, I'a,A ba2.
Разное количество групп в этих семействах связано с различным расположением порождающих разнородных плоскостей симметрии по отношению к цветным векторам: 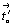 и и 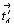 . .
Наиболее прост вывод групп антисимметрии с F-решеткой, поскольку двум федоровским группам - Fmm2 и Fdd2 - соответствуют две серые и такое же количество групп с единственной цветной решеткой - F'smm2 и F'sdd2. Действительно, взаимодействие чередующихся и тождественных между собой элементов симметрии (m  n(c n(c  b)) с цветными трансляциями F-группы приведет на обеих позициях символа к m b)) с цветными трансляциями F-группы приведет на обеих позициях символа к m  n n  c' c'  b'(c b'(c  b b  n' n'  m') (см. цветную вставку, рис. 169). В результате для класса C2v получены 12 полярных непримитивных групп, 12 нейтральных и 30 групп антисимметрии с цветными решетками. Остальные 30 групп, не содержащих антипереносов (цветных трансляций), легко вывести, <Щзацвечивая> порождающие элементы симметрии (см. табл. 8). m') (см. цветную вставку, рис. 169). В результате для класса C2v получены 12 полярных непримитивных групп, 12 нейтральных и 30 групп антисимметрии с цветными решетками. Остальные 30 групп, не содержащих антипереносов (цветных трансляций), легко вывести, <Щзацвечивая> порождающие элементы симметрии (см. табл. 8).
Геологический факультет МГУ
|


