|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2. Вывод и графическое представление трехмерных (пространственных) групп симметрии
Принцип вывода пространственных групп симметрии аналогичен тому, который использовался при выводе одномерных и двухмерных групп симметрии: приняв за исходные 32 точечные группы симметрии в рамках той или иной решетки Браве, выписываем для каждой из них все возможные сочетания порождающих макро- и микроэлементов симметрии. Этот принцип предложен Н.В. Беловым и в отечественной кристаллографической литературе получил название "классного", так как имелось в виду преподавание курса, посвященного пространственным группам, в высшей школе (в классе) для студентов, не имеющих фундаментальной математической подготовки [5, 18, 29].
VII.2.1. Вывод пространственных групп триклинной сингонии
Наиболее просто выписываются пространственные группы триклинной сингонии с единственно возможной примитивной решеткой Браве и единственным помимо осей 1-го порядка элементом макросимметрии, не имеющим пространственных разновидностей, - центром инверсии: Р1 (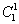 ) 1 и Р ) 1 и Р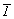 ( (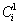 ) (обозначение центра инверсии см. на с. 5). ) (обозначение центра инверсии см. на с. 5).
Геологический факультет МГУ
|


