|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.1. Пространственные решетки.Типы решеток Браве
Если в трехмерном пространстве выбрать какую-либо точку (не обязательно материальную) и посчитать ее одним из узлов решетки, то в остальных ее узлах окажутся все точки этого пространства, идентичные (физически и геометрически) исходной. Прикладывая решетку к другой заинтересовавшей нас точке при сохранении параллельности решетки самой себе, в ее узлах вновь получим все эквивалентные точки. В результате убеждаемся, что решетка не нечто материальное (не конкретная укладка атомов в неподвижных узлах решетчатого каркаса), а математический образ - схема, с помощью которой мы описываем периодичность кристаллического вещества, не зависящая от того, какая точка трехмерного пространства (узора) принята за исходный узел. Иными словами, решетку удобно считать своеобразным элементом симметрии, размножающим точки пространства совершенно аналогично тому, как их размножают другие элементы симметрии - плоскости, оси и т.д. В этом смысле решетка - это выразитель кристаллического состояния вещества, ибо любое кристаллическое вещество, даже лишенное каких-либо иных элементов симметрии, всегда обладает этим основным элементом симметрии - решеткой, или решетчатым строением.
Как каждый единственный в своем роде элемент симметрии допускает только те элементы симметрии, которые переводят его в самого себя, так и решетка допускает присутствие только тех элементов симметрии исходной фигуры, которыми обладает она сама как геометрический образ. Поэтому, помимо размножения исходной фигуры присущими решетке трансляциями, она может передавать созданному бесконечному узору в соответствии с принципом Кюри (см. с. 65) симметрию исходной фигуры. Таким образом, для того чтобы весь узор приобрел симметрию исходной фигуры, в группу симметрии решетки должны входить в качестве подгруппы все элементы симметрии этой фигуры.
С другой стороны, как и всякая параллелепипедальная система, трехмерная решетка обладает рядом собственных симметрийных особенностей. Она всегда центросимметрична, при этом центры инверсии находятся как в узлах решетки - в вершинах параллелепипедов, так и на серединах расстояний между ними. Оси высших порядков неизбежно сопровождаются пересекающимися вдоль них плоскостями симметрии. Сами же оси симметрии ограничены только кристаллографическими порядками, т.е. n = 1, 2, 3, 4, 6 (см. с. 78). Последнее условие однозначно выбирает из бесконечного числа точечных групп, описывающих симметрию конечных исходных фигур, лишь 32 кристаллографические точечные группы.
Рассмотрим, какие по симметрии решетки способны передать бесконечной постройке симметрию любой из 32 точечных групп. Поскольку самая асимметричная фигура (с осью симметрии 1) не предъявляет каких-либо требований к симметрии решетки, может быть задействована решетка любой симметрии. Поэтому минимально возможной точечной группой симметрии рассматриваемой триклинной решетки будет 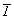 . Такая же решетка годится и для фигуры с собственной симметрией . Такая же решетка годится и для фигуры с собственной симметрией  . .
Фигуры с единственной осью симметрии 2-го порядка потребуют решетку с моноклинной симметрией  как результат взаимодействия данной оси с обязательным для пространственной решетки центром инверсии ( как результат взаимодействия данной оси с обязательным для пространственной решетки центром инверсии ( ). Естественно, что эта же решетка будет годна и для фигур с симметрией m и ). Естественно, что эта же решетка будет годна и для фигур с симметрией m и 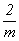 . .
Любая фигура, описываемая точечной группой ромбической сингонии - 222, mm2, mmm, передает свою симметрию бесконечной постройке с помощью решетки mmm (222 . 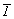 = mm2 . = mm2 . 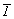 = = 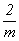 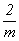 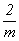 ). ).
Нетрудно убедиться, что любая из точечных групп тетрагональной сингонии (4, 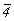 , , 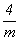 , 4mm, 422, , 4mm, 422, 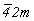 , , 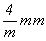 ) может быть передана бесконечному узору единственной решеткой, описываемой тетрагональной голоэдрической группой ) может быть передана бесконечному узору единственной решеткой, описываемой тетрагональной голоэдрической группой 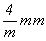 , ибо взаимодействие даже одной исходной оси 4 с обязательными для трехмерной решетки центром инверсии и плоскостями, пересекающимися вдоль этой оси, однозначно приведет к указанной группе. , ибо взаимодействие даже одной исходной оси 4 с обязательными для трехмерной решетки центром инверсии и плоскостями, пересекающимися вдоль этой оси, однозначно приведет к указанной группе.
Симметрия всех 12 групп гексагональной сингонии (3, 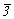 , 32, 3m, , 32, 3m, 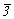 m, 6, m, 6, 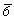 , , 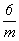 , 622, 6mm, , 622, 6mm, 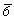 m2, m2, 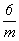 mm) может быть передана бесконечному узору решеткой гексагональной голоэдрии mm) может быть передана бесконечному узору решеткой гексагональной голоэдрии 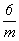 mm. Однако принцип минимума возможной симметрии позволяет для пяти групп с осями 3-го порядка - групп тригональной подсингонии (см. с. 41) - использовать решетку пониженной симметрии - гексагональной гемиэдрии: mm. Однако принцип минимума возможной симметрии позволяет для пяти групп с осями 3-го порядка - групп тригональной подсингонии (см. с. 41) - использовать решетку пониженной симметрии - гексагональной гемиэдрии: 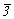 m (= тригональной голоэдрии). m (= тригональной голоэдрии).
Группы кубической сингонии (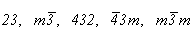 ) обслуживает решетка с симметрией m ) обслуживает решетка с симметрией m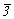 m. m.
В результате убеждаемся, что во всех случаях точечные группы симметрии решетки как геометрического образа отвечают старшему - голоэдрическому - классу каждой сингонии. Это накладывает соответствующие ограничения на выбор минимального по объему параллелепипеда повторяемости, с помощью которого можно охарактеризовать данную трехмерную постройку.
Трехмерная решетка может быть представлена тремя некомпланарными трансляционными векторами, а значит построенный на этих векторах параллелепипед - параллелепипед повторяемости - будет ячейкой решетки. Для того чтобы параллелепипед мог служить характеристической ячейкой какой-либо решетки, т.е. отражал бы ее главные симметрийные особенности, необходимо, чтобы его ребра (трансляционные векторы) совпали с особыми направлениями максимальной симметрии, т.е. с направлениями кристаллографических координатных осей (см. с. 41). Ячейку, выбранную таким образом, называют ячейкой Браве или элементарной ячейкой. Тип и симметрия ячейки отражаются в ее названии, которое она передает и соответствующей ей пространственной решетке. Поскольку форму ячейки Браве определяет координатный репер, семь разных по симметрии решеток (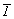 , ,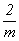 , mmm, , mmm, 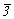 m, m, 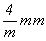 , , 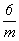 mm, m mm, m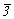 m) могут быть представлены шестью типами параллелепипедов (ибо гексагональные решетки обслуживаются одним и тем же координатным репером, а значит, и одинаковыми по форме ячейками Браве - параллелепипедами со 120-градусным ромбом в основании). m) могут быть представлены шестью типами параллелепипедов (ибо гексагональные решетки обслуживаются одним и тем же координатным репером, а значит, и одинаковыми по форме ячейками Браве - параллелепипедами со 120-градусным ромбом в основании).
Каждая ячейка Браве - параллелепипед повторяемости - характеризуется своими параметрами - константами решетки: тремя координатными векторами 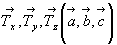 либо соответствующими им шестью скалярными величинами | либо соответствующими им шестью скалярными величинами | 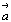 | , | | , | 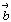 | , | | , | 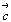 | и углами | и углами  = b^c, = b^c,  = a^c, = a^c,  = a^b. = a^b.
Иногда в качестве параллелепипеда повторяемости используют так называемую основную ячейку, построенную на трех последовательных минимальных трансляциях решетки: amin 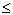 bmin bmin 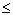 cmin. Однако собственная симметрия такого параллелепипеда не всегда полностью отражает главную особенность решетки - ее симметрию. Поэтому основная ячейка не всегда является ячейкой Браве. cmin. Однако собственная симметрия такого параллелепипеда не всегда полностью отражает главную особенность решетки - ее симметрию. Поэтому основная ячейка не всегда является ячейкой Браве.
Если ребра ячейки соответствуют трем последовательным минимальным трансляциям, т.е. узлы решетки располагаются только в вершинах параллелепипеда, то такая "пустая" ячейка ( и решетка) Браве называется примитивной и обозначается буквой Р.
Если же координатные трансляции ячейки Браве не соответствуют трем последовательным минимальным трансляциям, т.е. в ячейке есть более короткие (не координатные!) векторы 1, то в ней кроме вершинных окажутся дополнительные узлы. Указанная ячейка (а следовательно, и решетка) будет непримитивной.
Обратим внимание на то, что в вершинных узлах ячеек Браве как точках пересечения векторов максимальной симметрии будут сосредоточены все элементы симметрии соответствующей голоэдрической точечной группы. А так как дополнительные узлы связаны трансляциями с вершинными узлами и, следовательно, идентичны им, они могут располагаться лишь в таких позициях, в которых голоэдрический комплекс решетки представлен либо полностью, либо своей максимальной подгруппой, содержащей главную (или одну из главных) ось симметрии. Такие позиции находятся лишь в центрах граней или объема ячейки. Поэтому ячейки с дополнительными узлами принято называть центрированными. При этом наличие дополнительных узлов не нарушает симметрию решетки и не уменьшает ее объем.
Если в ячейке центрирована только одна пара противоположных граней (например, ее базис), то ячейку (и соответственно решетку) называют базоцентрированной и обозначают либо буквой С (центрированы грани (001) и (00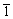 ) либо А (узлы на гранях (100) и ( ) либо А (узлы на гранях (100) и (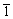 00)), либо В (узлы на гранях (010) и (0 00)), либо В (узлы на гранях (010) и (0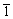 0). А- и В-ячейки можно назвать бокоцентрированными. 0). А- и В-ячейки можно назвать бокоцентрированными.
Одновременная центрировка двух пар граней (например, А и В) приводит к возникновению трансляции АВ, которая автоматически обеспечивает центрировку и грани С (рис. 59, а). Такие ячейки, в которых центрированы все грани, называются гранецентрированными и обозначаются буквой F. Ячейку с дополнительным узлом в центре ее объема называют объемноцентрированной и обозначают буквой I. Одновременная центрировка базиса ячейки и объема (рис. 59, б) или всех граней ячейки и объема приведет к появлению укороченных векторов (напри-мер, вектор IC), по которым можно выбрать примитивный параллелепипед меньшего объема.
Остановимся подробнее на некоторых моментах вывода решеток Браве, рассмотрев все возможные позиции для дополнительных узлов в элементарных ячейках всех сингоний (систем).
В решетке триклинной сингонии (a  b b  c, c,      ) (точечная группа симметрии ) (точечная группа симметрии 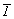 ) отсутствие особых направлений никаких ограничений на выбор ячейки Браве не накладывает, поэтому выбор характеристического параллелепипеда произволен. И любая триклинная ячейка может быть представлена одним из косоугольных параллелепипедов минимального объема без дополни-тельных узлов 2. Отсюда в списке возможных типов решеток триклинной сингонии будет лишь примитивная - Р (рис. 60). ) отсутствие особых направлений никаких ограничений на выбор ячейки Браве не накладывает, поэтому выбор характеристического параллелепипеда произволен. И любая триклинная ячейка может быть представлена одним из косоугольных параллелепипедов минимального объема без дополни-тельных узлов 2. Отсюда в списке возможных типов решеток триклинной сингонии будет лишь примитивная - Р (рис. 60).
В решетке моноклинной сингонии (a  b b  c , c ,  = =  = 90o , = 90o ,   90o 90o  120o ) (точечная группа симметрии 120o ) (точечная группа симметрии 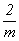 ) присутствие единст-венного особого направления, однозначно используемого в качестве одного из ребер элементарной ячейки, заставляет два других ребра выбирать по узловым рядам, хотя и не являющимся особыми направлениями, но лежащим в перпендикулярной особому направлению плоскости. Это определяет косоугольность лишь одной пары граней ячейки Браве. Поэтому для дополнительных узлов пригодны лишь позиции в центрах прямоугольных граней и в центре ячейки. Центрировка косоугольной грани не приведет к новой решетке (рис. 61, а), ибо в этой плоскости особые направления отсутствуют и ребра ячейки поэтому могут быть выбраны по любым узловым рядам. Центрировка одной из прямоугольных граней, т.е. появление дополнительного трансляционного вектора, приведет к оригинальной В- или А-решетке. К этим же решеткам приведет и центрировка объема ячейки. Отметим, что равенство объемов бокоцентрированной и объемноцентрированной ячеек Браве ни одной из них преимущества не дает, тогда как F-центрировка приводит к предпочтительности выбора ячейки меньшего размера - I или B(A) (рис. 61, а). ) присутствие единст-венного особого направления, однозначно используемого в качестве одного из ребер элементарной ячейки, заставляет два других ребра выбирать по узловым рядам, хотя и не являющимся особыми направлениями, но лежащим в перпендикулярной особому направлению плоскости. Это определяет косоугольность лишь одной пары граней ячейки Браве. Поэтому для дополнительных узлов пригодны лишь позиции в центрах прямоугольных граней и в центре ячейки. Центрировка косоугольной грани не приведет к новой решетке (рис. 61, а), ибо в этой плоскости особые направления отсутствуют и ребра ячейки поэтому могут быть выбраны по любым узловым рядам. Центрировка одной из прямоугольных граней, т.е. появление дополнительного трансляционного вектора, приведет к оригинальной В- или А-решетке. К этим же решеткам приведет и центрировка объема ячейки. Отметим, что равенство объемов бокоцентрированной и объемноцентрированной ячеек Браве ни одной из них преимущества не дает, тогда как F-центрировка приводит к предпочтительности выбора ячейки меньшего размера - I или B(A) (рис. 61, а).
Напомним, что помимо рассмотренной выше рациональной установки моноклинной ячейки, при которой по единственному особому направлению выбирается ось Z (угол моноклинности  - X^Y), нередко используется и классическая (минералогическая) установка с особым направлением вдоль оси Y и углом моноклинности - X^Y), нередко используется и классическая (минералогическая) установка с особым направлением вдоль оси Y и углом моноклинности  (X^Z), что меняет обозначение моноклинной ячейки: В(А)рац = С(А)мин (см. с. 40). (X^Z), что меняет обозначение моноклинной ячейки: В(А)рац = С(А)мин (см. с. 40).
В решетке ромбической сингонии (a  b b  c , c ,  = =  = = = 90o ) (точечная группа симметрии mmm) обязательное присутствие трех взаимно перпендикулярных неэквивалентных особых направлений диктует ортогональную координатную систему и, следовательно, обусловливает прямоугольную форму параллелепипеда Браве. Введение любого дополнительного узла в позицию с симметрией mmm (симметрия вершинного узла), т.е. в центры граней или объема, приведет к появлению дополнительных трансляций, не совпадающих с особыми направлениями, а следовательно, к непримитивным ячейкам Браве: С(А,В) - базо(боко)центрированной, F - гранецентрированной или I - объемноцентрированной (рис. 61, б). = 90o ) (точечная группа симметрии mmm) обязательное присутствие трех взаимно перпендикулярных неэквивалентных особых направлений диктует ортогональную координатную систему и, следовательно, обусловливает прямоугольную форму параллелепипеда Браве. Введение любого дополнительного узла в позицию с симметрией mmm (симметрия вершинного узла), т.е. в центры граней или объема, приведет к появлению дополнительных трансляций, не совпадающих с особыми направлениями, а следовательно, к непримитивным ячейкам Браве: С(А,В) - базо(боко)центрированной, F - гранецентрированной или I - объемноцентрированной (рис. 61, б).
В решетке тетрагональной сингонии (a = b  c , c ,  = =  = =  = 90o ) (точечная гр. сим. = 90o ) (точечная гр. сим. 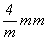 ) присутствие единственной оси 4-го порядка, вдоль которой выбирают координатную ось Z, делает эквивалентными два других перпендикулярных к ней особых направления X и Y, что и обусловливает форму ячейки в виде тетрагональной призмы. Выбор ребер a и b элементарной ячейки в первую очередь лимитируется минимальными трансляциями в плоскости, перпендикулярной оси 4-го порядка (оси Z). Это делает некорректным выбор базо- и гранецентрированных тетрагональных ячеек, которые являются лишь иными аспектами соответственно Р- и I-ячеек меньшего размера, т.е. С = Р, F = I. В итоге оригинальными окажутся лишь два типа тетрагональных решеток Браве: Р и I (рис. 61, в). ) присутствие единственной оси 4-го порядка, вдоль которой выбирают координатную ось Z, делает эквивалентными два других перпендикулярных к ней особых направления X и Y, что и обусловливает форму ячейки в виде тетрагональной призмы. Выбор ребер a и b элементарной ячейки в первую очередь лимитируется минимальными трансляциями в плоскости, перпендикулярной оси 4-го порядка (оси Z). Это делает некорректным выбор базо- и гранецентрированных тетрагональных ячеек, которые являются лишь иными аспектами соответственно Р- и I-ячеек меньшего размера, т.е. С = Р, F = I. В итоге оригинальными окажутся лишь два типа тетрагональных решеток Браве: Р и I (рис. 61, в).
В гексагональной сингонии (a = b  c , c ,  = =  = 90o , = 90o ,  = 120o ) одна и та же координатная система обслуживает две разные по симметрии решетки: = 120o ) одна и та же координатная система обслуживает две разные по симметрии решетки: 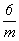 mm и mm и 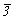 m - с одинаковой формой ячеек Браве. Ячейка собственно гексагональной подсингонии m - с одинаковой формой ячеек Браве. Ячейка собственно гексагональной подсингонии 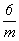 mm не допускает никакой центрировки, так как в ней отсутствуют позиции с симметрией вершинного узла. И указанная решетка может быть представлена лишь примитивным параллелепипедом Браве: Р (рис. 62, а). mm не допускает никакой центрировки, так как в ней отсутствуют позиции с симметрией вершинного узла. И указанная решетка может быть представлена лишь примитивным параллелепипедом Браве: Р (рис. 62, а).
Следует иметь в виду, что в старых изданиях учебников и Интернациональных таблиц [71] можно встретить иные обозначения типов гексагональных решеток. Поскольку гексагональной элементарной ячейкой считался не параллелепипед, построенный на трех координатных трансляциях, а гексагональная призма, в центре базисной грани которой оказывался узел решетки (рис. 62, б), то такая "базоцентрированная" ячейка обозначалась буквой С. Иногда в гексагональной решетке в качестве параллелепипеда повторяемости выбиралась также базоцентрированная, но ортогональная ячейка (a  b b  c , c ,  = =  = =  =90o , где b = a =90o , где b = a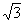 ) (рис. 62, в), которая обозначалась также буквой С. Однако все указанные решетки характеризуются одним и тем же примитивным параллелепипедом - ячейкой Браве - с параметрами a = b ) (рис. 62, в), которая обозначалась также буквой С. Однако все указанные решетки характеризуются одним и тем же примитивным параллелепипедом - ячейкой Браве - с параметрами a = b  c , c ,  = = = 90o , = 90o ,  =120o (рис. 62, а). Современное обозначение такой ячейки (и соответственно решетки) - Р. Кроме рассмотренных установок (и обозначений - С) нередко употреблялась дважды базоцентрированная ячейка Н (рис. 62, г), ребра которой расположены под углом 30o к координатным осям стандартной Р-ячейки, т.е. направлены по ее длинным диагоналям. Обращение к Н-ячейке снимает противоречие между классической кристаллографией, опирающейся на минералогию, требующую, чтобы в гексагональной сингонии за оси X и Y принимались направления, перпендикулярные к плоскости симметрии, и современным подходом к написанию символов гексагональных групп, при котором координатные оси выбираются по кратчайшим трансляциям и могут не совпадать с нормалями к плоскостям симметрии. В этом случае координатная позиция в символе группы оказывается пустой и заполняется единицей - символом оси 1-го порядка. Выбор укрупненной Н-ячейки формально удовлетворяет требованиям минералогов, переводя особое направление (нормаль к плоскости симметрии) на нужную - 2-ю - позицию символа. Например, Р31m = H3m1, P =120o (рис. 62, а). Современное обозначение такой ячейки (и соответственно решетки) - Р. Кроме рассмотренных установок (и обозначений - С) нередко употреблялась дважды базоцентрированная ячейка Н (рис. 62, г), ребра которой расположены под углом 30o к координатным осям стандартной Р-ячейки, т.е. направлены по ее длинным диагоналям. Обращение к Н-ячейке снимает противоречие между классической кристаллографией, опирающейся на минералогию, требующую, чтобы в гексагональной сингонии за оси X и Y принимались направления, перпендикулярные к плоскости симметрии, и современным подходом к написанию символов гексагональных групп, при котором координатные оси выбираются по кратчайшим трансляциям и могут не совпадать с нормалями к плоскостям симметрии. В этом случае координатная позиция в символе группы оказывается пустой и заполняется единицей - символом оси 1-го порядка. Выбор укрупненной Н-ячейки формально удовлетворяет требованиям минералогов, переводя особое направление (нормаль к плоскости симметрии) на нужную - 2-ю - позицию символа. Например, Р31m = H3m1, P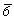 2m = H 2m = H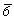 m2. m2.
Ячейка Браве тригональной подсингонии (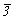 m) не может быть примитивной, так как в ней обязательно должны присутствовать дополнительные узлы, снижающие симметрию решетки от m) не может быть примитивной, так как в ней обязательно должны присутствовать дополнительные узлы, снижающие симметрию решетки от 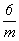 mm до mm до 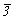 m . Такие узлы могут находиться лишь в позициях на осях 3-го порядка, проходящих через центры тригональных призм ячейки, т.е. в позициях с симметрией 3m (рис. 63, б). Это приводит к появлению новых векторов, не сокращающих координатные трансляции ячейки Браве. Таким образом, дополнительные узлы могут иметь лишь координаты m . Такие узлы могут находиться лишь в позициях на осях 3-го порядка, проходящих через центры тригональных призм ячейки, т.е. в позициях с симметрией 3m (рис. 63, б). Это приводит к появлению новых векторов, не сокращающих координатные трансляции ячейки Браве. Таким образом, дополнительные узлы могут иметь лишь координаты 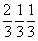 и и 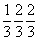 или или 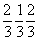 и и 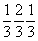 , т.е. располагаться на одной из длинных диагоналей ячейки в точках ее пересечения с осями 3-го порядка, делящих эту диагональ на три равные части. Появление в указанных позициях центров инверсии (их симметрия повысится до , т.е. располагаться на одной из длинных диагоналей ячейки в точках ее пересечения с осями 3-го порядка, делящих эту диагональ на три равные части. Появление в указанных позициях центров инверсии (их симметрия повысится до 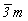 ) не нарушит симметрию решетки и не сократит ее координатные трансляции. Такую элементарную ячейку - ячейку Браве - и представляемую ею решетку называют дважды объемноцентрированной или, в соответствии с формой примитивного параллелепипеда повторяемости (но не ячейки Браве!) - ромбоэдра, ромбоэдрической - R (рис. 63, в). ) не нарушит симметрию решетки и не сократит ее координатные трансляции. Такую элементарную ячейку - ячейку Браве - и представляемую ею решетку называют дважды объемноцентрированной или, в соответствии с формой примитивного параллелепипеда повторяемости (но не ячейки Браве!) - ромбоэдра, ромбоэдрической - R (рис. 63, в).
В ячейке кубической сингонии (a = b = c ,  = =  = = =90o ) (точечная группа симметрии m =90o ) (точечная группа симметрии m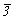 m) для дополнительных узлов кроме позиции с симметрией m m) для дополнительных узлов кроме позиции с симметрией m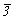 m в центре объема ячейки Браве, порождающей объемноцентрированную I-ячейку, легко выделяются позиции в центрах всех граней с симметрией максимальной подгруппы m в центре объема ячейки Браве, порождающей объемноцентрированную I-ячейку, легко выделяются позиции в центрах всех граней с симметрией максимальной подгруппы 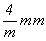 . Эти позиции связаны между собой четверкой осей 3-го порядка, что делает невозможной центрировку лишь одной пары граней. Предположив в этих позициях дополнительные узлы, мы тем самым повышаем их симметрию до симметрии вершинных узлов (m . Эти позиции связаны между собой четверкой осей 3-го порядка, что делает невозможной центрировку лишь одной пары граней. Предположив в этих позициях дополнительные узлы, мы тем самым повышаем их симметрию до симметрии вершинных узлов (m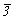 m) и при этом убеждаемся, что они не нарушают ни координатные трансляции, ни симметрию всей решетки. Таким образом, имеем 3 типа решеток кубической сингонии: Р, I и F (см. рис. 61, г). m) и при этом убеждаемся, что они не нарушают ни координатные трансляции, ни симметрию всей решетки. Таким образом, имеем 3 типа решеток кубической сингонии: Р, I и F (см. рис. 61, г).
Геологический факультет МГУ
|


