|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IV.4. Взаимодействие зеркальной плоскости симметрии и перпендикулярной к ней трансляции
Результат взаимодействия зеркальной плоскости симметрии с перпендикулярной к ней трансляцией наглядно иллюстрируется модельным способом (рис. 25). Последовательно проведенные операции симметрии - отражение в плоскости my и последующий перенос на
величину вектора 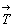 y - переведут исходную фигуру 1 в положение 2 и затем 3. Поскольку фигуры 1 и 3 оказываются энантиоморфными, то результирующая операция симметрии, их связывающая, будет операцией 2-го рода, задаваемой плоскостью симметрии m' y, проходящей между этими фигурами параллельно иcходной плоскости my и отстоящей от нее на половину заданного трансляционного вектора - y - переведут исходную фигуру 1 в положение 2 и затем 3. Поскольку фигуры 1 и 3 оказываются энантиоморфными, то результирующая операция симметрии, их связывающая, будет операцией 2-го рода, задаваемой плоскостью симметрии m' y, проходящей между этими фигурами параллельно иcходной плоскости my и отстоящей от нее на половину заданного трансляционного вектора - 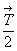 . .
Другое, аналитическое доказательство [18] рассматривает перемещение произвольной точки с координатами mnp относительно начала координат, взятого на зеркальной плоскости my, перпендикулярной вектору 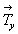 = a (рис. 25). Отражение в плоскости my приведет к точке с координатами = a (рис. 25). Отражение в плоскости my приведет к точке с координатами 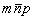 , а дальнейший ее перенос на трансляционный вектор переведет ее в положение с координатами m,a- n,p (где a - абсолютное значение вектора , а дальнейший ее перенос на трансляционный вектор переведет ее в положение с координатами m,a- n,p (где a - абсолютное значение вектора 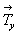 ). Координаты исходной и конечной точек связаны отражением в зеркальной плоскости, расположенной на середине вектора ). Координаты исходной и конечной точек связаны отражением в зеркальной плоскости, расположенной на середине вектора 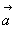 . Из анализа рассмотренного взаимодействия можно сделать следующий вывод: любая трансляция может быть заменена двумя последовательными отражениями в двух зеркальных плоскостях, перпендикулярных к ней. При этом расстояние между этими плоскостями равно половине трансляции; расположение же первой из этих плоскостей произвольно. . Из анализа рассмотренного взаимодействия можно сделать следующий вывод: любая трансляция может быть заменена двумя последовательными отражениями в двух зеркальных плоскостях, перпендикулярных к ней. При этом расстояние между этими плоскостями равно половине трансляции; расположение же первой из этих плоскостей произвольно.
Таким образом, трансляция не только размножает (транслирует) элементы симметрии (в данном случае зеркальную плоскость), но и взаимодействует с ними. В результате появляется новый неэквивалентный исходному элемент симметрии на ее середине, что хорошо видно на рисунке Эшера (рис. 26).
Геологический факультет МГУ
|


