|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IV.2. Взаимодействие оси симметрии и параллельной ей трансляции. Винтовые оси симметрии
Рассмотрим сочетание двух операций симметрии 1-го рода - поворота вокруг оси 4-го порядка и одновременного переноса в параллельном оси направлении, т.е. взаимодействие поворота с трансляцией вдоль оси Z [18]. Размножив произвольно взятую точку (фигуру) вокруг вертикальной оси 4-го порядка - 4z (рис. 21, а), получим четыре эквивалентные точки 1 - 4. Трансляция 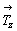 размножит эти точки в направлении координатной оси Z: из точки 1 получим точки 1' , 1' ' , 1' ' ' , 1' ' ' ' и т.д., из точки 2 - 2' , 2' ' , 2' ' ' и т.д. В результате возникнут четверки точек на одном уровне по оси Z: 1' , 2' , 3 ' , 4' и т.д., связанные поворотом на 90o вокруг исходной оси 4; точки же, расположенные друг над другом - 1, 1' , 1' ' , ..., - связаны вертикальным трансляционным вектором размножит эти точки в направлении координатной оси Z: из точки 1 получим точки 1' , 1' ' , 1' ' ' , 1' ' ' ' и т.д., из точки 2 - 2' , 2' ' , 2' ' ' и т.д. В результате возникнут четверки точек на одном уровне по оси Z: 1' , 2' , 3 ' , 4' и т.д., связанные поворотом на 90o вокруг исходной оси 4; точки же, расположенные друг над другом - 1, 1' , 1' ' , ..., - связаны вертикальным трансляционным вектором 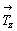 . Для того чтобы от точки 1 перейти к точке 2' , понадобятся две последовательные операции: поворот вокруг оси 4-го порядка на 90o против часовой стрелки с одновременной трансляцией вдоль оси Z. Поскольку кристаллографические группы - это частный случай математических абстрактных групп, в которых произведение симметрических операций группы рассматривается как самостоятельная операция, принадлежащая этой же группе, в данном случае будет иметь место новая симметрическая операция 1-го рода - винтовой поворот - и соответственно новый элемент симметрии, задающий такое сочетание симметрических операций, - винтовая ось симметрии. Таким образом, в данном случае поворотная ось 4-го порядка одновременно является и винтовой осью этого же порядка. Если порождающие элементы симметрии - поворотную ось 4 и трансляцию . Для того чтобы от точки 1 перейти к точке 2' , понадобятся две последовательные операции: поворот вокруг оси 4-го порядка на 90o против часовой стрелки с одновременной трансляцией вдоль оси Z. Поскольку кристаллографические группы - это частный случай математических абстрактных групп, в которых произведение симметрических операций группы рассматривается как самостоятельная операция, принадлежащая этой же группе, в данном случае будет иметь место новая симметрическая операция 1-го рода - винтовой поворот - и соответственно новый элемент симметрии, задающий такое сочетание симметрических операций, - винтовая ось симметрии. Таким образом, в данном случае поворотная ось 4-го порядка одновременно является и винтовой осью этого же порядка. Если порождающие элементы симметрии - поворотную ось 4 и трансляцию 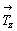 - убрать, то их произведение - винтовая ось симметрии - сохранится в чистом виде (рис. 21, б). При этом винтовое движение можно разложить на две в общем случае "мнимые" симметрические операции: поворот вокруг не существующей поворотной оси 4-го порядка и перенос, не являющийся трансляцией в этом направлении, т.е. элементом симметрии. Истинная же трансляция - убрать, то их произведение - винтовая ось симметрии - сохранится в чистом виде (рис. 21, б). При этом винтовое движение можно разложить на две в общем случае "мнимые" симметрические операции: поворот вокруг не существующей поворотной оси 4-го порядка и перенос, не являющийся трансляцией в этом направлении, т.е. элементом симметрии. Истинная же трансляция 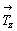 в кратное число раз ( в данном случае в 4 раза) превысит величину исходного (мнимого!) переноса в кратное число раз ( в данном случае в 4 раза) превысит величину исходного (мнимого!) переноса 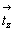 . Из рис. 21, б видно, что поворот на 90o вокруг "мнимой" поворотной оси 4-го порядка сопровождается переносом вдоль нее на вектор, называемый ходом винтовой оси. Четырехкратное винтовое движение приведет к точке 1' ' ' ' , связанной с точкой 1 истинной трансляцией в этом направлении . Из рис. 21, б видно, что поворот на 90o вокруг "мнимой" поворотной оси 4-го порядка сопровождается переносом вдоль нее на вектор, называемый ходом винтовой оси. Четырехкратное винтовое движение приведет к точке 1' ' ' ' , связанной с точкой 1 истинной трансляцией в этом направлении 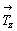 = 4 = 4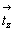 . Порядок винтовой оси определяется, как и в случае поворотных осей, элементарным углом поворота . Порядок винтовой оси определяется, как и в случае поворотных осей, элементарным углом поворота  . В данном случае имеет место винтовая ось 4-го порядка - 41. . В данном случае имеет место винтовая ось 4-го порядка - 41.
Разнообразие винтовых осей одного и того же порядка, связанное с величинами векторов 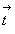 , отражено в их международных обозначениях: винтовые оси обозначаются арабскими цифрами, соответствующими порядку оси, с нижним цифровым индексом, указывающим, какой части истинной трансляции , отражено в их международных обозначениях: винтовые оси обозначаются арабскими цифрами, соответствующими порядку оси, с нижним цифровым индексом, указывающим, какой части истинной трансляции 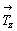 соответствует трансляционный вектор соответствует трансляционный вектор 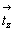 винтовой оси. Например, если винтовой оси. Например, если 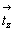 = = 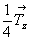 , а вращение происходит против часовой стрелки на 90o , то винтовая ось обозначается 41 (рис. 21, б) и называется "правой". Энантиоморфная ей ось с вращением в противоположную сторону (по часовой стрелке) называется "левой" и обозначается 4-1 или 43 , так как правое вращение в данном случае сопровождается переносом , а вращение происходит против часовой стрелки на 90o , то винтовая ось обозначается 41 (рис. 21, б) и называется "правой". Энантиоморфная ей ось с вращением в противоположную сторону (по часовой стрелке) называется "левой" и обозначается 4-1 или 43 , так как правое вращение в данном случае сопровождается переносом 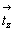 = = 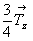 (рис. 21, в). (рис. 21, в).
Если же 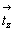 = =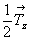 , то винтовая ось 42 оказывается нейтральной, ибо направление вращения не играет в данном случае существенной роли (рис. 21, г). , то винтовая ось 42 оказывается нейтральной, ибо направление вращения не играет в данном случае существенной роли (рис. 21, г).
Графически вертикальные винтовые оси изображаются соответствующими их порядку многоугольниками с "лопастями", указывающими на направление вращения:
Геологический факультет МГУ
|


