Теория симметрии кристаллов

Глава IV. Операции и элементы симметрии бесконечных закономерных построек и их взаимодействия

Рис. 19

IV.1. Трансляция как основной элемент симметрии бесконечных построек

Трансляция - симметрическая операция 1-го рода бесконечных объектов, сохраняющая неизменной метрику исходной фигуры, - является параллельным переносом в одном направлении и на одинаковое рас-стояние, при котором каждой точке ис-ходной фигуры соответствует анало-гичная точка другой фигуры (рис. 19).

Рис. 20

Трансляцией помимо операции симметрии часто называют и тот элемент симметрии бесконечных закономерно построенных объектов, который задает операцию переноса.

Взаимодействия трансляционных векторов

Многократное повторение трансляции + 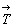вдоль одной прямой создает одномерную бесконечную постройку (узор) из трансляционно идентичных исходных фигур. Такое повторение приводит к появлению новых, увеличенных в кратное число раз трансляционных векторов 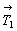, 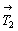и т.д. в этом же направлении (рис. 20, а).

Сочетание трансляций - некол-линеарных векторов (в общем случае 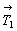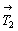) - также приводит к появлению нового, легко вычисляемого по правилу параллелограмма суммарного вектора (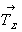) и, таким образом, к бесконечному двухмерному узору (рис. 20, б).

См. также Завершилась III Всероссийская научная школа "Математические исследования в кристаллографии, минералогии и петрографии" Изучение упругих свойств минералов при высоких давлении и температуре на примере вюстита и железо-никелевого сплава: Изучение упругих свойств минералов при высоких давлении и температуре на примере вюстита и железо-никелевого сплава: Глава 1. Литературный обзор. Теория упругости в применении к минеральным фазам Земли. ПРЕДПОЛАГАЕМЫЙ МЕХАНИЗМ РОСТА ХАЛЦЕДОНА. Peter J. Heaney.