|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
I.2.2. Операции и элементы симметрии конечных фигур 2-го рода
Отражение в плоскости, оставляющее неподвижными только точки пространства, лежащие в этой плоскости, называемой зеркальной плос-костью симметрии, связывает зеркально равные - энантиоморфные - фи-гуры или их части (рис. 1, б). Обозначают эти элементы симметрии в сим-волике Браве буквой P, в международной символике - m, графически - жирной или двойной линией.
Центр инверсии - это "зеркальная точка", инвертируясь ("отражаясь") в которой правая фигура превращается в левую, как в фокусе оптической линзы. При этом "отражении" остается неподвижной только одна точка пространства. Обозначается центр инверсии буквой С (по Браве), 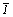 (в международной символике) или буквой i, графически - кружком (o ) (в международной символике) или буквой i, графически - кружком (o ) (рис. 1, в). (рис. 1, в).
Если поворот вокруг оси n-го порядка на угол -  (рис. 2, а) сопроводить операцией симметрии 2-го рода - отражением в плоскости симметрии, перпендикулярной оси вращения, то возникнет "сложный" элемент симметрии - зеркально-поворотная ось, включающая эти две операции симметрии. Однако, несмотря на то, что каждая из совместных операций "работает", реальных элементов симметрии, задающих эти операции, в общем случае нет, т.е. они мнимые. Эти операции симметрии коммутируют, иными словами, последовательность их действий безразлична. Обозначаются зеркальные оси по Браве символом (рис. 2, а) сопроводить операцией симметрии 2-го рода - отражением в плоскости симметрии, перпендикулярной оси вращения, то возникнет "сложный" элемент симметрии - зеркально-поворотная ось, включающая эти две операции симметрии. Однако, несмотря на то, что каждая из совместных операций "работает", реальных элементов симметрии, задающих эти операции, в общем случае нет, т.е. они мнимые. Эти операции симметрии коммутируют, иными словами, последовательность их действий безразлична. Обозначаются зеркальные оси по Браве символом 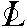 n и в международной символике - n и в международной символике - 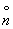 . .
Например, из рис. 3, на котором изображено действие зеркально-поворотной оси 4-го порядка - 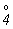 , видно, что расположение фигур не подчинено ни вертикальной поворотной оси 4-го порядка (4), ни перпендикулярной ей горизонтальной плоскости симметрии (P , видно, что расположение фигур не подчинено ни вертикальной поворотной оси 4-го порядка (4), ни перпендикулярной ей горизонтальной плоскости симметрии (P ), ни вообще каким бы то ни было реальным элементам симметрии или их сочетаниям. И в какой бы последовательности ни проводить эти операции: сначала поворот, потом отражение или наоборот - результат будет одинаков. Поскольку ось ), ни вообще каким бы то ни было реальным элементам симметрии или их сочетаниям. И в какой бы последовательности ни проводить эти операции: сначала поворот, потом отражение или наоборот - результат будет одинаков. Поскольку ось 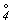 оригинальна (незаменима), она имеет специальное графическое обозначение: оригинальна (незаменима), она имеет специальное графическое обозначение:  . .
На рис. 4, а показан результат действия зеркальной оси 6-го порядка (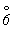 ), где также обе операции, характеризующие эту сложную ось, - поворот на 60o и отражение в плоскости, перпендикулярной этой оси, - мнимые. Однако в данном случае можно увидеть иные реальные элементы симметрии: поворотную ось, но уже 3-го (а не 6-го) порядка и центр инверсии. Сочетание этих операций можно рассматривать и как действие сложной оси иного характера. В самом деле, поворот вокруг оси n-го порядка на угол ), где также обе операции, характеризующие эту сложную ось, - поворот на 60o и отражение в плоскости, перпендикулярной этой оси, - мнимые. Однако в данном случае можно увидеть иные реальные элементы симметрии: поворотную ось, но уже 3-го (а не 6-го) порядка и центр инверсии. Сочетание этих операций можно рассматривать и как действие сложной оси иного характера. В самом деле, поворот вокруг оси n-го порядка на угол  (см. рис. 2, б), сопровождающийся операцией инверсии - "отражением в точке", расположенной на этой оси, - характеризует сложный элемент симметрии, называемый инверсионной осью, включающей также две в общем случае мнимые операции симметрии. Обозначаются инверсионные оси (см. рис. 2, б), сопровождающийся операцией инверсии - "отражением в точке", расположенной на этой оси, - характеризует сложный элемент симметрии, называемый инверсионной осью, включающей также две в общем случае мнимые операции симметрии. Обозначаются инверсионные оси 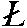 n или n или 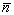 . .
На рис. 4, б показаны фигуры, расположение которых подчинено действию инверсионной оси 6-го порядка (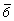 ). Очевидно, что здесь отсутствуют и реальная поворотная ось 6-го порядка, и центр инверсии. Однако, как и в случае зеркальной оси 6-го порядка, можно увидеть реальные (другие!) элементы симметрии: поворотную ось 3-го порядка и зеркальную плоскость, перпендикулярную этой оси. Таким образом, и зеркальная ( ). Очевидно, что здесь отсутствуют и реальная поворотная ось 6-го порядка, и центр инверсии. Однако, как и в случае зеркальной оси 6-го порядка, можно увидеть реальные (другие!) элементы симметрии: поворотную ось 3-го порядка и зеркальную плоскость, перпендикулярную этой оси. Таким образом, и зеркальная (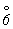 ) и инверсионная ( ) и инверсионная (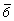 ) оси 6-го порядка в отличие от оси ) оси 6-го порядка в отличие от оси 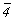 не являются оригинальными, т.е. могут быть заменены простыми элементами симметрии, и поэтому специальных графических обозначений они не требуют. не являются оригинальными, т.е. могут быть заменены простыми элементами симметрии, и поэтому специальных графических обозначений они не требуют.
Обобщив рассмотренные примеры и обратившись к рис. 2, в, можно сделать вывод о том, что каждой зеркальной оси с элементарным углом поворота a соответствует инверсионная ось с элементарным углом поворота  = 180o - = 180o -  . При этом вращения вокруг обеих осей направлены в противоположные стороны: . При этом вращения вокруг обеих осей направлены в противоположные стороны:
 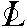 1 1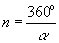 = = 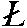 -1 -1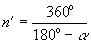 . .
Подставив в приведенную формулу значения элементарных углов поворота оставшихся не рассмотренными кристаллографических осей 1-го, 2-го и 4-го порядков, обнаружим, что 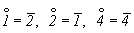 . Нетрудно также убедиться, что действия сложных осей 1-го порядка и соответствующих им сложных осей 2-го порядка эквивалентны действию простых элементов симметрии ( . Нетрудно также убедиться, что действия сложных осей 1-го порядка и соответствующих им сложных осей 2-го порядка эквивалентны действию простых элементов симметрии (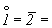 P P и и 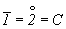 ), ибо поворотная компонента сложной оси 1-го порядка ( ), ибо поворотная компонента сложной оси 1-го порядка ( = 360o) равна нулю, и, следовательно, вторая операция - зеркальное отражение или инверсия в точке - оказывается действительной, а не мнимой. = 360o) равна нулю, и, следовательно, вторая операция - зеркальное отражение или инверсия в точке - оказывается действительной, а не мнимой.
Из вышеизложенного ясно, что внешняя симметрия любого многогранника может быть описана с помощью только осей симметрии - простых (поворотных) и (или) сложных (зеркальных или инверсионных), взаимодействие которых составляет суть "осевой" теоремы Эйлера.
Геологический факультет МГУ
|


