|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
I.2.1. Oперации и элементы симметрии конечных фигур 1-го рода
Поворотная ось симметрии - это прямая, при повороте вокруг которой на определенный угол фигуры или равные части одной фигуры занимают в пространстве положения, эквивалентные исходному. Наименьший угол поворота  , приводящего фигуру к самосовмещению, называется элементарным углом поворота оси симметрии, величина которого определяет порядок оси n, т.е. число самосовмещений фигуры при полном ее повороте o на 360o ( n = 360o/ , приводящего фигуру к самосовмещению, называется элементарным углом поворота оси симметрии, величина которого определяет порядок оси n, т.е. число самосовмещений фигуры при полном ее повороте o на 360o ( n = 360o/ ) (рис. 1, а). Сама же операция поворота некоторой фигуры есть одинаковое угловое смещение ее точек относительно оси поворота - прямой, точки которой остаются неподвижными при данном симметрическом преобразовании. ) (рис. 1, а). Сама же операция поворота некоторой фигуры есть одинаковое угловое смещение ее точек относительно оси поворота - прямой, точки которой остаются неподвижными при данном симметрическом преобразовании.
Оси симметрии в символике Браве обозначаются буквой L с нижним цифровым индексом n, соответствующим порядку оси (Ln), либо, в международной символике (символике Германа - Могена, см. с. 366), арабскими цифрами, указывающими на порядок оси (например, L1 = 1, L2 = 2, L3 = 3 и т.д.). Графически поворотные оси симметрии изображаются многоугольниками:
L2 - сферическим двуугольником (фюзо) 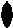 , L3 - , L3 -  , L4 - , L4 -  , L6 - , L6 -  . .
Иногда при обозначении операций симметрии к символу оси добавляют показатель степени, соответствующий числу повторенных операций. При этом знак "минус" указывает на обратное действие (например, поворот в противоположном направлении). Так, если 41 - поворот вокруг оси 4-го порядка против часовой стрелки на 90o, то 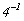 ( = 43) - поворот на этот же угол по часовой стрелке. ( = 43) - поворот на этот же угол по часовой стрелке.
В геометрических фигурах возможны поворотные оси симметрии любых порядков. В кристаллах же порядок оси ограничен: n = 1, 2, 3, 4, 6, что является следствием их "решетчатого" строения (доказательство см. на с. 78 - 79).
Геологический факультет МГУ
|


