Моделирование - это метод изучения объекта или процесса, в ходе которого исследуется не сам объект, а некоторая вспомогательная, созданная нами система, называемая моделью. Модель должна обладать свойством адекватности и адаптивности исследуемым процессам в отношении некоторых заданных критериев.
С чего начинается построение физико-химической (термодинамической) модели? Прежде всего необходимо построить качественную геологическую (геохимическую и т.п.) модель процесса, которая аккумулирует в себе теоретические представления о нем, конкретные природные и экспериментальные данные. Геологическая модель может описывать как процесс в целом, так и отдельные явления, входящие в него. Однако создать количественную теорию геохимических процессов и решить проблемы геохимической практики чисто индуктивным путем, т.е. только по результатам геологических наблюдений, без привлечения законов физической химии, невозможно.
Физико-химическая модель отражает взаимосвязи компонентов геологической модели с помощью термодинамических соотношений (в том числе условий химических равновесий), динамики тепло- и массопереноса, кинетики химических взаимодействий.
Математическая модель количественно описывает соотношения физико-химической модели с помощью системы уравнений и ограничений (условия минимальности термодинамического потенциала, уравнения тепло- и массопереноса, кинетические ограничения и т.д.) и включает в себя методы и алгоритмы ее решения.
Каждая из моделей может развиваться относительно независимо, но только их сочетание дает количественную модель объекта или процесса. Численное моделирование позволяет исследовать физико-химическую модель процесса, а также при наличии нескольких альтернативных моделей выбрать наиболее адекватно отображающую реально наблюдаемые закономерности. Несоответствие результатов численного моделирования и данных по реальному прототипу заставляет корректировать физико-химическую модель или ставить вопрос об изменениях в геологической модели процесса.
Наиболее активно в настоящее время развивается моделирование на основе равновесной термодинамики с использованием быстродействующих ЭВМ. Именно такое моделирование будем в дальнейшем называть термодинамическим. Для получения количественной информации с помощью термодинамической модели процесса нужно:
1) создать геологическую модель процесса или явления2; 2) иметь достаточное количество исходной термодинамической информации для описания системы; 3) располагать математическим алгоритмом и его реализацией в виде программы на ЭВМ. В последние 30 лет идет интенсивное накопление разнообразной термодинамической информации для различных природных соединений: минералов, частиц водного раствора, газов. Необходимость исследования сложных многокомпонентных гетерогенных систем, появление быстродействующих ЭВМ и развитие методов математического программирования предопределили качественный скачок: создание высокоэффективных вычислительных программ для расчета на ЭВМ равновесий в сложных химических системах.
Важным методологическим вопросом исследования геохимических систем является взаимосвязь экспериментального изучения и количественного термодинамического моделирования. В настоящее время стало ясно, что прямое экспериментальное моделирование сложных природных процессов практически невозможно. Главными препятствиями на пути эксперимента являются многокомпонентность природных систем, время их существования и функционирования, метастабильность многих реакций в эксперименте, неизбежность упрощения и изменения систем, необходимость получения большого числа экспериментальных точек, огромное время, требующееся для этого и т.п.
Термодинамическое моделирование на ЭВМ практически не имеет этих ограничений и может выступать как альтернатива моделирующего эксперимента. В то же время экспериментальные исследования являются "питательной средой" термодинамического моделирования. Экспериментальное изучение простых систем с точно контролируемыми параметрами дает необходимые данные для получения надежных термодинамических характеристик минералов, частиц водных растворов, газов и т.д. Большое значение имеют также опорные экспериментальные исследования достаточно сложных систем, которые в случае их безусловной надежности являются хорошим контролем данных количественного термодинамического расчета.
Методологической основой моделирования геохимических явлений, основанного на методах термодинамики равновесных процессов, является положение о существовании в геохимических системах частичных или локальных равновесий. Понятие частичного равновесия означает, что в неравновесной в целом геохимической системе, характеризующейся множеством химических реакций, может выполняться химическое равновесие для отдельной (или отдельных) реакции. Это означает, что данная реакция релаксирует к химически равновесному состоянию быстрее изменения внешних переменных параметров и других реакций. Понятие частичного равновесия является временным. Локальное равновесие в системе устанавливается тогда, когда фазы, находящиеся в контакте, обратимо взаимодействуют друг с другом (например, такое равновесие может установиться по границам зерен). На основе принципа локальных равновесий неравновесную в целом геохимическую систему часто можно разделить на ряд пространственных участков, для которых в данный момент времени выполняются условия химического равновесия. Такие отдельные участки системы находятся друг с другом в неравновесных состояниях, и это в целом обеспечивает неравновесность крупных геохимических систем. Понятие локального равновесия является пространственным.
Вероятность существования частичных и локальных равновесий неодинакова в гомогенных и гетерогенных геохимических системах. Скорости реакций в гомогенных системах настолько велики, что системы могут приближаться к химически равновесным состояниям при изменении внешних условий достаточно быстро. Так, растворенные формы углекислоты релаксируют к равновесным состояниям практически мгновенно. Даже для окислительно-восстановительных процессов скорости релаксации в геологическом понимании велики.
Более сложны гетерогенные системы с межфазовыми взаимодействиями. Но и в их пределах существуют частичные и локальные равновесия. Они возникают при уменьшении скоростей фильтрации подземных вод и длительном времени межфазовых взаимодействий и неизменных внешних условиях.
Термодинамическое моделирование начинается с выделения системы. Реальные геохимические системы в принципе открыты, т.е. в них возможен обмен с внешней средой веществом и энергией. Однако часто конкретные задачи термодинамического моделирования могут формулироваться как для открытых, так и для закрытых систем (без обмена с внешней средой веществом) в зависимости от целей исследования. Выделение исследователем системы и ее границ определяет и подходы к интерпретации результатов термодинамического моделирования.
Моделирование процесса на основе равновесной термодинамики с применением принципов локального и частичного равновесия заключается в том, что состояние системы, в которой протекает процесс, описывается через определенным образом построенную последовательность равновесных состояний системы. Динамика и кинетика природных процессов, отражающие неравновесность и необратимую эволюцию природных систем во времени и пространстве, должны быть сведены в таком методе моделирования к закономерностям изменения валовых химических составов и условий существования последовательных равновесных состояний.
Даже в наиболее простом взаимодействии "вода-конгруэнтно растворяющийся минерал" эволюция системы проходит через последовательные стадии. Определенный круг проблем необратимой эволюции систем может быть решен путем расчета равновесий при использовании принципов частичного и локального равновесия. Существует несколько общих методических приемов, применяемых для расчетов необратимой эволюции систем.
Наибольшее распространение в опубликованных работах по термодинамическому моделированию природных процессов получил метод степени протекания реакции (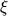 -метод). Этот метод предложен Г.Хелгесоном в 1969 г. и развит в работах И.К. Карпова и других. Данный метод в своем изначальном виде был разработан для описания процессов в закрытой системе (а также в системах с вполне подвижным компонентом, химический потенциал которых задан извне). В ряде исследований этот метод был непосредственно использован для моделирования зональности метасоматических колонок без каких-либо оговорок (работы С.А.Кашика, И.К.Карпова, В.А.Копейкина, М.Рида и др.). Рассмотрение существа -метод). Этот метод предложен Г.Хелгесоном в 1969 г. и развит в работах И.К. Карпова и других. Данный метод в своем изначальном виде был разработан для описания процессов в закрытой системе (а также в системах с вполне подвижным компонентом, химический потенциал которых задан извне). В ряде исследований этот метод был непосредственно использован для моделирования зональности метасоматических колонок без каких-либо оговорок (работы С.А.Кашика, И.К.Карпова, В.А.Копейкина, М.Рида и др.). Рассмотрение существа 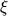 -метода показывает, что это не всегда правомерно [Борисов, Гричук, 1988]. Если моделируются процессы при фильтрации раствора через породу, то в таком процессе вторичные минералы выходят из контакта с той порцией раствора, с которой они равновесны (а это в -метода показывает, что это не всегда правомерно [Борисов, Гричук, 1988]. Если моделируются процессы при фильтрации раствора через породу, то в таком процессе вторичные минералы выходят из контакта с той порцией раствора, с которой они равновесны (а это в 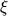 -методе не реализуется). Теоретический анализ и численное моделирование показали, что -методе не реализуется). Теоретический анализ и численное моделирование показали, что 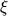 -метод дает правильные сведения о составе раствора и набор вторичных минералов только в случае образования простой метасоматической колонки, т.е. когда в каждой последующей зоне происходит увеличение числа минералов на единицу и ни один из выпавших минералов далее не растворяется. Эти условия соблюдаются, как правило, в тех случаях, когда исходный раствор не содержит компонентов, переходящих в твердую фазу (кроме самой H2O). В таких моделях -метод дает правильные сведения о составе раствора и набор вторичных минералов только в случае образования простой метасоматической колонки, т.е. когда в каждой последующей зоне происходит увеличение числа минералов на единицу и ни один из выпавших минералов далее не растворяется. Эти условия соблюдаются, как правило, в тех случаях, когда исходный раствор не содержит компонентов, переходящих в твердую фазу (кроме самой H2O). В таких моделях 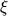 -метод может применяться и для моделирования метасоматической зональности. Если это условие не выполняется, то применение -метод может применяться и для моделирования метасоматической зональности. Если это условие не выполняется, то применение 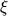 -метода дает растянутые зоны существования растворяющихся вторичных минералов, искаженные составы растворов и даже ложные минеральные ассоциации. -метода дает растянутые зоны существования растворяющихся вторичных минералов, искаженные составы растворов и даже ложные минеральные ассоциации.
Дальнейшее развитие 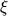 -метод получил в работах Б.Фрица и Ш.Фуйяка и других, которые представили метасоматическую колонку в виде последовательности "боксов". При расчете эволюции такой составной системы на каждом шаге по lg -метод получил в работах Б.Фрица и Ш.Фуйяка и других, которые представили метасоматическую колонку в виде последовательности "боксов". При расчете эволюции такой составной системы на каждом шаге по lg 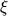 происходит изменение составов системы вследствие переноса части раствора, получившегося в предшествующем "боксе" на предыдущем шаге ("обновляемая система"). Было показано, что этот метод дает результаты, отличные от классического происходит изменение составов системы вследствие переноса части раствора, получившегося в предшествующем "боксе" на предыдущем шаге ("обновляемая система"). Было показано, что этот метод дает результаты, отличные от классического 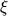 -метода, если перенос массы (скорость фильтрации) существенно больше скорости взаимодействия. -метода, если перенос массы (скорость фильтрации) существенно больше скорости взаимодействия.
Для анализа динамических систем с привносом и выносом компонентов разработан метод ступенчатых проточных реакторов. В нем система разбивается на серию отдельных подсистем - реакторов. Исходный раствор вступает в реакцию с породой в первом реакторе, результирующий раствор перемещается во второй реактор и вступает в реакцию с породой, находящейся там, и т.д. Таким образом, порция раствора меняет свой состав, переходя через серию реакторов, и изменяет состав породы в них. Последовательное прохождение порций раствора формирует в породе (совокупности реакторов) метасоматическую колонку. Количество породы в каждом реакторе зависит от соотношения скоростей фильтрации и взаимодействия в системе "раствор-порода".
Метод ступенчатых реакторов представляет собой переход к равновесно-динамическим моделям. Система реакторов может быть сконструирована различными способами: масса породы в реакторах может быть одинаковой или разной; система может быть изотермической или политермической, изобарической или полибарической и т.д. Выбор той или иной системы определяется задачей исследования и принятой геологической моделью объекта.
2Поскольку речь идет о гидротермальном минералообразовании, то геологическая модель должна включать в себя и модель гидродинамическую (структуры потоков гидротерм на изучаемом объекте).
Геологический факультет МГУ
 |
ЕЖЕГОДНЫЙ СЕМИНАР ПО ЭКСПЕРИМЕНТАЛЬНОЙ МИНЕРАЛОГИИ, ПЕТРОЛОГИИ И ГЕОХИМИИ (ЕСЭМПГ-2006).Программа семинара. 18-19 апреля 2006 г. |
|
 |
Фазовые отношения во фторсодержащей гранитной и нефелин-сиенитовой системах и распределение элементов между фазами: ЗАКЛЮЧЕНИЕ |
|
|
|
|
|
|


