|
2.1. Модели массопереноса в гомогенной среде
В гомогенной среде модель переноса включает в себя модельное описание конвективного переноса и микродисперсии.
2.1.1. Конвективный перенос
В модели конвективного переноса используется схема поршневого вытеснения, в которой принимается, что все частицы воды двигаются в каждом сечении с одинаковой скоростью. Найдем в такой постановке выражение для скорости перемещения границы раздела (фронта вытеснения) растворов сорбируемых мигрантов, разделяющих области с концентрациями в воде с и с0, при условии мгновенного наступления сорбционного равновесия (т.е. без учета кинетики сорбции), составляя балансовое уравнение мигранта в бесконечном малом элементе трубки тока dl, который проходит граница раздела растворов мигранта за время dt:
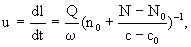 (2.1) (2.1)
где Q-расход потока в трубки тока, N и N0-содержания сорбированного мигранта в единичном объеме породы, соответствующие концентрациям раствора с и с0 , 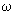 -площадь поперечного сечения трубки тока. При линейном уравнении сорбции вида (1.9) имеем (N-N0)/(c-c0)= -площадь поперечного сечения трубки тока. При линейном уравнении сорбции вида (1.9) имеем (N-N0)/(c-c0)=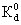 , где , где 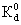 -объемный коэффициент распределения, так что уравнение (2.1) принимает вид -объемный коэффициент распределения, так что уравнение (2.1) принимает вид
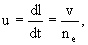 nе =n0 + nе =n0 +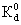 , (2.2) , (2.2)
где v - скорость фильтрации на границе раздела (фронте поршневого вытеснения), nе - т.н. эффективная пористость, характеризующая суммарную емкость породы для рассматриваемого мигранта. Для нейтрального мигранта nе=n0 и величина u равняется средней действительной скорости фильтрации u0 =v/n0.
Решение уравнения (2.2) производится интегрированием по направлениям траекторий течения, которые должны предварительно строится на основе геофильтрационных расчетов, проводимых в общем случае с использованием методов численного моделирования (Мироненко, Румынин, т.1, 1998).
При стационарном режиме потока траектории совпадают с линиями тока, а расчеты конвективного переноса по лентам тока удобно проводить, определяя значения интервалов времени 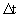 , за которые мигрант переносится на расстояние , за которые мигрант переносится на расстояние 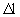 , в пределах которого известна разница напоров , в пределах которого известна разница напоров 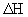 . При градиенте напора . При градиенте напора 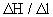  из уравнения (2.2) получим для из уравнения (2.2) получим для 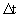 выражение выражение
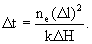 (2.3) (2.3)
При конвективном теплопереносе, рассматривая таким же путем баланс тепла в бесконечно малом элементе длиной dl, получим аналогичное выражение для скорости конвективного теплопереноса
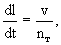 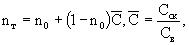 (2.4) где Сск - объемная теплоемкость скелета породы, (2.4) где Сск - объемная теплоемкость скелета породы, 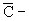 относительная объемная теплоемкость породы. Используя данные, приведенные в работе (Чеверев, 2004), можно ориентировочно принимать для известняков относительная объемная теплоемкость породы. Используя данные, приведенные в работе (Чеверев, 2004), можно ориентировочно принимать для известняков 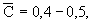 для глинистых пород для глинистых пород 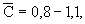 для мелкозернистых и пылеватых песков для мелкозернистых и пылеватых песков 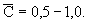
Сопоставляя (2.4) и (2.2) можно видеть, что формально расчетные зависимости для скорости конвективного массо-и теплопереноса оказываются идентичными и переходят друг в друга, если положить nе = nт.
2.1.2. Модель конвективно-дисперсионного переноса
При наложении конвективного и дисперсионного переноса суммарный единичный массовый поток jм будет
jм = jк + jd (2.5)
где jк определяется из (1.1), а jd для микродисперсии определяется выражением (1.3), где в фильтрационном потоке Dм заменяется на коэффициент гидродисперсии Dl.
Теоретическое описание такого процесса проведем для одномерного переноса в фильтрационном потоке со скоростью фильтрации v в направлении l при записи (2.5) в форме
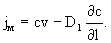 (2.6) (2.6)
Балансовое уравнение для нейтрального мигранта запишем, составляя его баланс в бесконечно малом элементе длиной 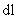 и единичной площади поперечного сечения, что после преобразований дает и единичной площади поперечного сечения, что после преобразований дает
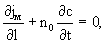 (2.7) (2.7)
где n0 - активная пористость породы.
Подставляя в (2.7) выражение (2.6) для jм , получим дифференциальное уравнение одномерного конвективно-дисперсионного переноса
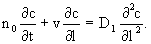 (2.8) (2.8)
При наличии обменных (сорбционных) процессов, уравнение неразрывности (2.7) примет вид
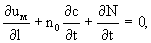 (2.9) (2.9)
где N- количество мигранта (в размерности концентрации с), сорбированного в единичном объеме породы. Тогда уравнение переноса будет
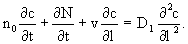 (2.10) (2.10)
Для замыкания (2.10) к нему следует добавить уравнение кинетики сорбции в форме (1.11).
При прогнозных расчетах длительно протекающих процессов в гомогенных породах обычно можно пренебречь кинетикой сорбции (Шестаков, 1969) и тогда 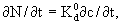 где где 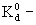 объемный коэффициент распределения. Тогда уравнение (2.10) принимает форму уравнения (2.8), в котором только активная пористость n0 заменяется на эффективную пористость nе , определяемую согласно (2.2). объемный коэффициент распределения. Тогда уравнение (2.10) принимает форму уравнения (2.8), в котором только активная пористость n0 заменяется на эффективную пористость nе , определяемую согласно (2.2).
По этому в дальнейшем, считая возможным принимать условие пренебрежения кинетикой сорбции, будем рассматривать уравнения и решения для переноса нейтральных мигрантов, имея в виду, что они могут использоваться и для расчетов переноса сорбируемых мигрантов, если заменить активную пористость n0 на эффективную пористость nэ, определяемую согласно (2.2).
При проявлениях процессов деструкции мигранта в уравнении баланса добавляется член скорости деструкции , который обычно задается уравнением необратимой кинетики первого порядка (1.12) и тогда уравнение конвективно-дисперсионного переноса будет
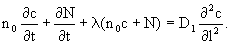 (2.19) (2.19)
При этом уравнение кинетики сорбции принимает вид:
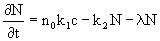 . (2.20) . (2.20)
При совместном действии конвективного и кондуктивного теплопереноса потоки тепла представляются выражениями (1.2) и (1.6). Вводя эти выражения в уравнение одномерного теплового потока. получим дифференциальное уравнение для распределения температуры 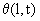 : :
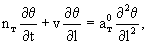 (2.21) (2.21)
Параметр 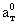 связан с коэффициентом температуропроводности породы ат соотношением связан с коэффициентом температуропроводности породы ат соотношением 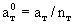 . Обобщая данные опытных определений, приведенных в работе (Чеверев, 2004), можно рекомендовать пользоваться в качестве типичных следующими значениями ат: . Обобщая данные опытных определений, приведенных в работе (Чеверев, 2004), можно рекомендовать пользоваться в качестве типичных следующими значениями ат:
порода известняк песчаник суглинок песок
ат,м2/сут 0,03-0,17 0,04-0,2 0,03-0,05 0,05-0,1
Сопоставление дифференциальных уравнений (2.21) и (2.8) свидетельствуют о их аналогии, причем они совпадают если заменить 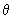 на с, nт на n0 и D на aт . на с, nт на n0 и D на aт .
В дифференциальных уравнениях многомерного переноса зависимость коэффициента дисперсии от компонентов скорости фильтрации в декартовых координатах имеет тензорную форму. Для плоских потоков можно существенно упростить форму дифференциальных уравнении переноса записывая их в системе криволинейных координат потенциала скорости фильтрации и функции тока (Мироненко, Румынин, том 1, 1998).
2.1.3. Фундаментальная задача конвективно-дисперсионного переноса
Рассмотрим решение дифференциального уравнения (2.8) для условий фундаментальной задачи переноса мигрантов в одномерном потоке по направлению 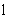 при начальной постоянной концентрации с0 и изменении ее на входной границе ( при начальной постоянной концентрации с0 и изменении ее на входной границе (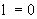 ) до величины с0. ) до величины с0.
Преобразуем прежде всего уравнение (2.8), вводя в него интегральное преобразование по Лапласу-Карсону 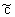 =L(с): =L(с):
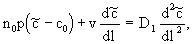 (2.22) (2.22)
где p - параметр преобразования (Шестаков, 1995). Решение уравнения (2.22) при условии 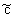 = с0 на границе = с0 на границе 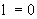 полуограниченного потока имеет вид полуограниченного потока имеет вид
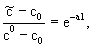 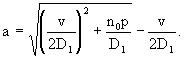 (2.23) (2.23)
Переход от этого изображения к оригиналу при с0 =соnst дает выражение (Лукнер, Шестаков, 1986).
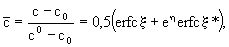 (2.24) (2.24)
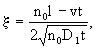 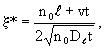 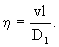 (2.24а) (2.24а)
Решения задач двух и трехмерного переноса в одномерном фильтрационном потоке приведены в работах (Лукнер, Шестаков, 1986; Мироненко, Румынин, 1998).
Расчеты по уравнению (2.24) показывают, что через некоторое время после начала процесса формируются три основные миграционные зоны: вытесняющего мигранта (с относительной концентрацией 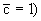 , переходная , переходная 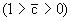 и начального содержания мигранта ( и начального содержания мигранта (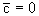 ). В это время второй член уравнения (2.24) оказывается пренебрежимо малым, и тогда можно пользоваться упрощенным выражением для относительной концентрации: ). В это время второй член уравнения (2.24) оказывается пренебрежимо малым, и тогда можно пользоваться упрощенным выражением для относительной концентрации:
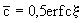 (2.25) (2.25)
при относительной погрешности, оцениваемой по формуле 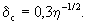
Из анализа решения фундаментальной задачи можно получить представление об особенностях проявления конвективной и дисперсионной форм переноса. Из выражения (2.25) следует, что на фронте поршневого вытеснения, определяемом только конвективным переносом, где 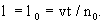 получаем получаем 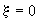 и и 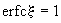 , так что здесь , так что здесь 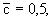 т.е. положение фронта поршневого вытеснения соответствует середине переходной зоны со средней концентрацией между вытесняющим и вытесняемым растворами. Размер переходной зоны, возникающей за счет влияния микродисперсии, характеризуется величиной т.е. положение фронта поршневого вытеснения соответствует середине переходной зоны со средней концентрацией между вытесняющим и вытесняемым растворами. Размер переходной зоны, возникающей за счет влияния микродисперсии, характеризуется величиной 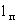 , на которую передняя граница переходной зоны обгоняет фронт поршневого вытеснения. Считая, что передняя граница переходной зоны соответствует относительной концентрации , на которую передняя граница переходной зоны обгоняет фронт поршневого вытеснения. Считая, что передняя граница переходной зоны соответствует относительной концентрации 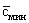 , по таблице функции erfc при , по таблице функции erfc при 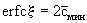 найдем соответствующее значение найдем соответствующее значение 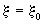 и получим формулу и получим формулу
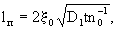 (2.26) (2.26)
причем
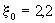 при при 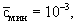 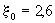 при при 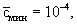 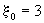 при при 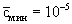 . (2.26а) . (2.26а)
Вычислительный эксперимент по оценке влияния продольной микродисперсии (молекулярной диффузии и гидродисперсии), проводимый исходя из оценки относительных размеров переходной зоны, показывает, что в лабораторных условиях микродисперсия может играть существенную роль, тогда как в натурных потоках влияние продольной микродисперсии оказывается пренебрежимо малым (Шестаков, 1995).
Решение фундаментальной задачи для системы дифференциальных уравнений (2.19 -2.20), учитывающих кинетику сорбции, деструкцию и микродисперсию в изображениях по Лапласу-Карсону 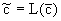 для относительной концентрации мигранта для относительной концентрации мигранта 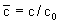 имеет вид имеет вид
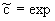 (-a0 (-a0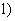 , (2.27) , (2.27)
где величина a0 получается решением квадратного уравнения
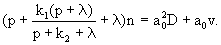 (2.27а) (2.27а)
Обращение этого выражения к оригиналу при D=0 (без учета микродисперсии)и с0 =const представляется выражением
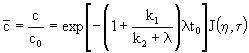 , (2.28) , (2.28)
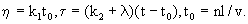 (2.28а) (2.28а)
Таблица функции Гольдштейна 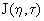 приведена, например, в книге (Лукнер, Шестаков, 1986). приведена, например, в книге (Лукнер, Шестаков, 1986).
2.2. Модели массопереноса в гетерогенно-блоковой среде
Для горных пород характерна гетерогенность различных масштабов - от кристаллической решетки до массива, - причем для описания процессов переноса наиболее значимой является гетерогенность масштаба порядка десятков сантиметров, обусловленная литофациальный изменчивостью и трещиноватостью горных пород. Для ее учета при построении теоретической модели переноса используется расчетная схема (модель) гетерогенно-блоковой среды (ГБС) или среды с двойной емкостью, представляющей собой квазиоднородную систему слабопроницаемых блоков, равномерно прорезаемых проводящими каналами.
В карбонатных породах такие каналы представлены наиболее крупными трещинами (объемное содержание порядка 1%), а блоки -весьма слабопроницаемым карбонатным материалом с пористостью 10-15%. Такая гетерогенно-блоковая среда называется также порово-трещинной. В глинистых породах повышенная проницаемость проводящих каналов объясняется наличием зон более грубого материала, а также повышенной трещиноватостью, причем емкость каналов и блоков может не иметь резкого различия. Сложное гетерогенное среда глинистых пород выявлена при изучении миграции амония в юрских глинах, где обнаружена высокая скорость миграции органических веществ сопоставимая со скоростью переноса нейтральных мигрантов (Лехов, Соколов, 2002).
В модели гетерогенно-блоковой среды перенос в каналах осуществляется конвективным путем, а в блоках-диффузионным и частично конвективным путями. Рассматривая перенос в блоке, выделим квазистационарный период, когда диффузионный перенос в пределах блока можно рассчитывать по схеме сосредоточенной емкости, усредняя ("размазывая") распределение мигранта внутри блока, т.е. считая емкость блока как бы сосредоточенной в его центре (ГБС 1-го типа). В начальный же период, когда на поток внутриблокового переноса не влияет размер блока, емкость которого можно считать неограниченной (ГБС 2-го типа). Критерии применимости этих схем, получаемые исходя из упрощенных представлений о строении блоков, из-за влияния неоднородности пород по размерам и внутреннему строению блоков могут дать лишь весьма приближенные оценки, так что реальные условия применимости схем ГБС 1-го и 2-го типов можно устанавливать только на основание диагностического анализа натурных экспериментов.
2.2.1.ГБС 1-го типа-с сосредоточенной емкостью блоков
Прототипом модели ГБС 1-го типа является модель двойной (дифференциальной) пористости среды, которая представляется в виде системы проходных и застойных ("тупиковых") пор при интенсивности обмена между ними пропорциальной разнице концентрации мигрантов между этими видами пор (Голубев, 1981). Для лучшего понимания процесса внутреннего обмена целесообразно представить обоснование такой модели на основе блокового строения пород, что открывает возможности оценки связей параметра массообмена с геометрическими характеристиками гетерогенности среды. Наиболее полное и ясное физическое представление о гетерогенно-блоковой среде с сосредоточенной емкостью дает рассмотрение квазиоднородной мозаично-блоковой среды, состоящей из системы блоков, равномерно прорезаемых проницаемыми каналами, причем конвективный поток в извилистых проницаемых каналах равномерно обтекает слабопроницаемые блики и частично протекает через них (Шестаков. 1995). Таким образом, в этой модели предполагается, что продольный перенос в проводящих каналах осуществляется только конвективным путем, а обмен между каналами и блоками - диффузионным и кондуктивным по схеме сосредоточенной емкости блока.
Для вывода дифференциальных уравнений такой квазиоднородной модели выделяется представительный элемент (объемом V), включающий в себя блок (объемом Vб ) и каналы (объемом Vк ). Обозначая относительные объемы каналов к=Vк /V и блоков 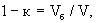 при концентрации мигранта в каналах с и в блоках c* содержание мигранта в представительном элементе будет: в каналах сn0 V, в блоке с*n*V, причем в дисперсной породе n0 = кnк , n*=(1-к)nб , где nк и nб - пористость каналов и блоков породы. Для сорбируемых мигрантов в величины пористости включается также характеристики сорбционной емкости породы. при концентрации мигранта в каналах с и в блоках c* содержание мигранта в представительном элементе будет: в каналах сn0 V, в блоке с*n*V, причем в дисперсной породе n0 = кnк , n*=(1-к)nб , где nк и nб - пористость каналов и блоков породы. Для сорбируемых мигрантов в величины пористости включается также характеристики сорбционной емкости породы.
Согласно закону Фика (1.3) запишем выражение для расхода поступления мигрантов в блок диффузионным путем:
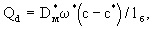 (2.29) (2.29)
где 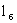 -расчетное расстояние от поверхности до центра блока; -расчетное расстояние от поверхности до центра блока; 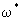 -площадь боковой поверхности блока; -площадь боковой поверхности блока; 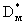 - коэффициент молекулярной диффузии в блоке. Конвективным путем происходит перенос в блоке при скорости фильтрации - коэффициент молекулярной диффузии в блоке. Конвективным путем происходит перенос в блоке при скорости фильтрации 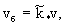 где где 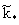 относительная проницаемость блока; v-средняя скорость фильтрации потока, так что расход конвективного поступления солей в блок определяется выражением относительная проницаемость блока; v-средняя скорость фильтрации потока, так что расход конвективного поступления солей в блок определяется выражением
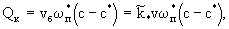 (2.29а) (2.29а)
где 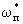 - площадь поперечного сечения блока. - площадь поперечного сечения блока.
Уравнение баланса мигранта в блоке будет
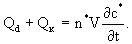 (2.30) (2.30)
Подставляя в(2.30) выражения Qd и Qк из (2.29) и (2.29а), получим дифференциальное уравнение внутреннего (внутриблокового) массообмена
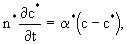 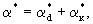 (2.31) (2.31)
где 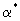 -коэффициент массообмена, составляющие которого -коэффициент массообмена, составляющие которого 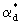 и и 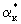 отражают действие диффузионного и конвективного переноса в блоках, причем отражают действие диффузионного и конвективного переноса в блоках, причем
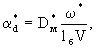 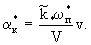 (2.31а) (2.31а)
В такой модели величина коэффициента массообмена оказывается линейно зависящий от скорости фильтрации v. Считая V~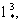 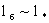 и и 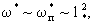 где где 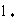 -расчетный размер представительного элемента, можно выразить структуру составляющих коэффициента массообмена в форме -расчетный размер представительного элемента, можно выразить структуру составляющих коэффициента массообмена в форме
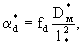 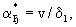 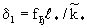 (2.31б) (2.31б)
где fd и fк -параметры, зависящие от формы блоков. В частности, для блоков кубической формы 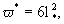 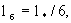 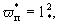 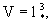 так что здесь получается fd =36 и fк =1. так что здесь получается fd =36 и fк =1.
В дополнение к уравнению внутриблокового обмена следует записать уравнение массопереноса для всего представительного элемента потока объемом V. Пренебрегая в нем дисперсией и учитывая относительно малую проницаемость блока, получим такое уравнение в виде (Шестаков, 1995):
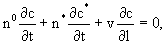 (2.32) (2.32)
Система уравнений (2.32) и (2.31) составляет теоретическую модель массопереноса в гетерогенно-блоковой среде в направлении 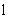 . .
Для многомерного потока записанного в системе декартовых координат дифференциальное уравнение (2.32) принимает вид
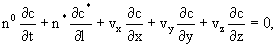 (2.33) (2.33)
где vx , vу, vz - компоненты скорости фильтрации. При этом уравнение массообмена (2.31) сохраняет свою форму при 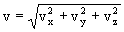
Фундаментальное решение системы уравнений (2.32) и (2.31) при постоянных значениях скорости фильтрации и параметров массопереноса с краевыми условиями для функции 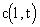 - начальном - начальном 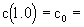 const и граничном с(0,t)=с0 ,- записываемое для относительной концентрации const и граничном с(0,t)=с0 ,- записываемое для относительной концентрации 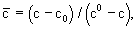 в изображениях по Лопласу-Карсону в изображениях по Лопласу-Карсону 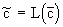 имеет вид: имеет вид:
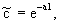 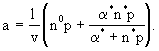 (2.34) (2.34)
Оригинал такого решения будет (Мироненко, Румынин, том1, 1998)
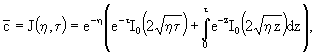 (2.35) (2.35)
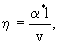 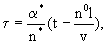 (2.35а) (2.35а)
Таблица функции Гольдштейна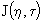 приведена, например, в книге (Лукнер, Шестаков, 1986). приведена, например, в книге (Лукнер, Шестаков, 1986).
При значительном времени развития процесса в таком потоке образуются зоны вытесняющего и вытесняемого раствора с переходной зоной между ними, а решение фундаментальной задачи принимает вид (Лукнер, Шестаков, 1986):
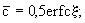 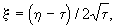 (2.36) (2.36)
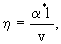 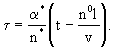 (2.36а) (2.36а)
Решение (2.36) рекомендуется применять при 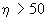 . .
Анализ этого решения дает возможность оценить размер переходной зоны распространения расчетного нейтрального мигранта 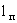 , приняв в этих выражениях , приняв в этих выражениях 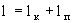 при размере зоны конвективного переноса при размере зоны конвективного переноса 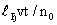 , где n0= , где n0=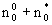 -суммарная активная пористость породы. Считая величину с пренебрежимо малой при значении -суммарная активная пористость породы. Считая величину с пренебрежимо малой при значении 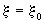 , после алгебраических преобразований получим выражение , после алгебраических преобразований получим выражение
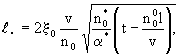 (2.37) (2.37)
а при 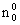 << n0 и t >> << n0 и t >> 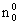 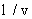 получится получится
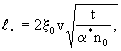 (2.37а) (2.37а)
причем величина 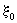 здесь такая же, как и в (2.26а). здесь такая же, как и в (2.26а).
При расчетах по модели ГБС-1-го типа при пренебрежимо малом проявлении микродисперсии существует передний фронт переноса мигрантов, ограничивающий область их распространения. Положение этого фронта получаются расчетами конвективного переноса при расчетной пористости каналов n0.
Для теплопереноса аналогичное уравнение теплообмена в блоках, связывающее температуры 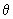 и и 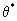 в каналах и блоках, имеет вид: в каналах и блоках, имеет вид:
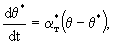 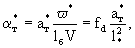 (2.38) где (2.38) где 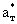 - температуропроводность породы блока. - температуропроводность породы блока.
Уравнение общего теплового баланса будет:
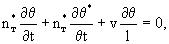 (2.39) где (2.39) где 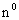 и и 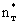 - значения nт , определяемые из (2.4) для каналов и блоков. - значения nт , определяемые из (2.4) для каналов и блоков.
Сопоставление уравнений (2.38) и (2.39) с аналогичными уравнениями массопереноса (2.31) и (2.32) показывает, что они совпадают, если заменить с на 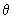 , n0 и n* на , n0 и n* на 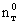 и и 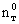 , , 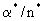 на на 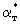 , причем величина , причем величина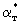 при при 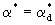 связана с величиной связана с величиной 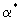 соотношением соотношением 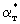 / /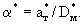
2.2.2. ГБС 2-го типа с неограниченной емкостью блоков
При больших размерах элементов неоднородности в начальный период развития процесса переноса применима схема гетерогенной среды с неограниченной емкостью блоков, в которой предполагается, что диффузионный перенос развивается только на периферической части блоков вблизи их поверхности. Для такой схемы диффузионной уравнение переноса мигрантов с концентрацией с для линейного потока со скоростью фильтрации будет (Лукнер, Шестаков, 1986; Мироненко, Румынин, 1998):
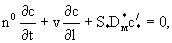 (2.40) (2.40)
где n0 - пористость (активная или эффективная) каналов, 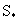 - удельная (в единице объема породы) поверхность блоков, - удельная (в единице объема породы) поверхность блоков, 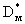 - коэффициент молекулярной диффузии блоков, - коэффициент молекулярной диффузии блоков, 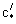 - градиент концентрации на поверхности блоков. Для изображении - градиент концентрации на поверхности блоков. Для изображении 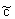 по Лапласу-Карсону величины с при нулевом начальном условии это уравнение принимает вид по Лапласу-Карсону величины с при нулевом начальном условии это уравнение принимает вид
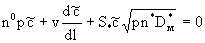 (2.41) (2.41)
Решение этого уравнения при граничном условии 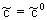 при при 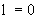 и начальном нулевом условии будет и начальном нулевом условии будет
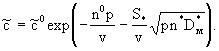 (2.42) (2.42)
Решение уравнения (2.40) в условиях фундаментальной задачи при начальном условии с=с0 дает для относительной концентрации выражение
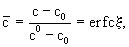 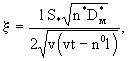 (2.43) (2.43)
причем 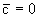 при при 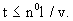
2.2.3. Поперечная макродисперсия в гетерогенно-блоковой среде
Для модельного описания поперечной макродисперсии целесообразно, исходя из представления породы, как гетерогенно-блоковой среды, использование модели "просеивания" мелких частиц через сетку крупных "фильтрующих" зерен (Письмен и др. 1967). На такой модели для точечной подачи мелких частиц установлено следующее распределение их концентрации в плоском потоке:
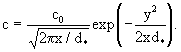 (2.44) (2.44)
где с0 -исходная концентрация; x и у- координаты по направлению просеивания (фильтрации) и перпендикулярно к нему; 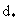 - диаметр фильтрующих зерен, соответствующий размеру блоков. - диаметр фильтрующих зерен, соответствующий размеру блоков.
Сопоставим с (2.44) выражение, полученное решением задачи конвективно-дисперсионного переноса, дающим распределение концентрации в потоке, двигающемся со скоростью v без продольной дисперсии, но с поперечной, характеризуемой коэффициентом Dт , при действии в начале координат источника постоянной интенсивности P=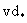 c0 . Такое решение дает для концентрации мигранта выражение (Лукнер, Шестаков, 1986): c0 . Такое решение дает для концентрации мигранта выражение (Лукнер, Шестаков, 1986):
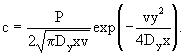 (2.44а) (2.44а)
где Dy =Dт - коэффициент поперечной дисперсии (в направлении у). Сопоставляя выражения (2.44) и (2.44а), можно видеть их идентичность, причем они тождественно совпадают, если положить
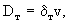 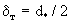 . (2.45) . (2.45)
Считая форму блоков кубической и идентифицируя диаметр зерен 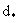 с размером блока с размером блока 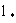 , можно связать величину , можно связать величину 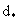 с коэффициентом диффузионного массопереноса с коэффициентом диффузионного массопереноса 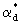 согласно (2.31б). Принимая для блоков кубической формы fd =36, получим таким образом соотношение согласно (2.31б). Принимая для блоков кубической формы fd =36, получим таким образом соотношение
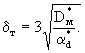 (2.45а) (2.45а)
2.2.4. Дисперсионные модели переноса в гетерогенной среде
Для описания макродисперсии в гетерогенной среде широко используется "дисперсионная (диффузионная) модель", представляемая дифференциальными уравнениями конвективно-дисперсионного переноса в гомогенной среде с некоторыми расчетными коэффициентами продольной и поперечной макродисперсии (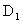 и Dт ) зависящими от строения среды (Лукнер, Шестаков, 1986; Орадовская, 1982; Мироненко, Румынин, том1, 1998) Для коэффициента продольной дисперсии рекомендуется выражение и Dт ) зависящими от строения среды (Лукнер, Шестаков, 1986; Орадовская, 1982; Мироненко, Румынин, том1, 1998) Для коэффициента продольной дисперсии рекомендуется выражение
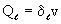 , (2.46) где , (2.46) где 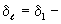 дисперсивность-параметр, величина которого задается по данным натурных исследований. дисперсивность-параметр, величина которого задается по данным натурных исследований.
Обоснование такой расчетной модели для продольной макродисперсии можно, в частности, получить сопоставляя выражения размеров переходной зоны (2.37а) и (2.26) соответственно для гетерогенно-блоковой среды 1-го типа и для гомогенной среды. Эти выражения согласуются, если связать коэффициент продольной макродисперсии 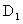 с коэффициентом внутреннего обмена с коэффициентом внутреннего обмена 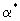 соотношением соотношением
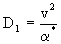 , (2.47) , (2.47)
где v-скорость фильтрации. На основе этого соотношения открывается возможность для понимания структуры зависимости коэффициента макродисперсии 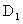 от скорости фильтрации v, если использовать для от скорости фильтрации v, если использовать для 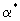 выражения (2.31а,б). Таким образом получается, что при малых скоростях фильтрации, когда выражения (2.31а,б). Таким образом получается, что при малых скоростях фильтрации, когда 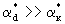 , должно быть , должно быть 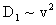 , а выражая , а выражая 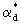 из (2.31б) через характерный размер блоков из (2.31б) через характерный размер блоков 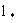 получим получим
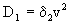 , , 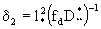 (2.48) (2.48)
В частности по данным опытно-миграционных работ, проведенных в опоках и песчаниках эоценового горизонта Зауралья, (Манукьян, Штенгелов, 1972) получено значение 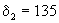 сут,что при сут,что при 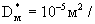 сут соответствует характерному размеру блока сут соответствует характерному размеру блока 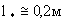 . .
При больших скоростях фильтрации, когда 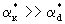 , согласно (2.31б) , согласно (2.31б)
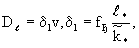 (2.49) (2.49)
что соответствует выражению (1.4) для гидродисперсии при 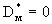 . .
В дисперсионной модели обычно используется зависимость для коэффициента продольной дисперсии вида (2.49), причем величина 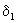 носит название дисперсивность и определяется на основании обобщения данных натурных наблюдений. носит название дисперсивность и определяется на основании обобщения данных натурных наблюдений.
Такие условия характерны для солепереноса при рассолении орошаемых земель и при опытах с монолитами пород. Имеющиеся опытные данные обработки полевых материалов промывок дают сравнительно близкие значения 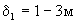 (Айдаров, 1985). При характерных для супесчано-суглинистых отложений значение (Айдаров, 1985). При характерных для супесчано-суглинистых отложений значение 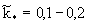 получим, что такие значения получим, что такие значения 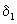 отвечают размерам блоков порядка отвечают размерам блоков порядка 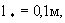 что соответствует размерам зоны неоднородности пород, фиксируемым по данным фильтрационных опробований. При таких размерах блоков согласно (2.24) имеет что соответствует размерам зоны неоднородности пород, фиксируемым по данным фильтрационных опробований. При таких размерах блоков согласно (2.24) имеет 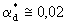 сут-1 , а при характерных для условий промывок орошаемых земель значениях v=0,01-0,1м/сут и сут-1 , а при характерных для условий промывок орошаемых земель значениях v=0,01-0,1м/сут и 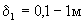 получим наиболее вероятный диапазон значений получим наиболее вероятный диапазон значений 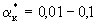 сут-1 . сут-1 .
Для установления связи между коэффициентами поперечной и продольной макродисперсии обратимся к выражению для Dт полученному по схеме "просеивания" частиц, используя связь коэффициента продольной макродисперсии 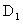 с коэффициентом массообмена с коэффициентом массообмена 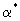 = =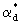 согласно (2.47). Подставляя выражения для согласно (2.47). Подставляя выражения для 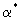 из (2.47) в (2.46), получим формулу, связывающую коэффициенты поперечной и продольной макродисперсии из (2.47) в (2.46), получим формулу, связывающую коэффициенты поперечной и продольной макродисперсии
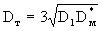 . (2.50) . (2.50)
Рациональные области применения дисперсионной модели для описания продольного переноса являются дискуссионными. Анализ показывает, что при реальных размерах элементов неоднородности дисперсионная модель продольной макродисперсии имеет ограниченное применение, поскольку расчетная величина коэффициента макродисперсии 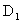 получается функцией времени, причем эта функция оказывается неповторимой во всех точках наблюдений. Сомнительна также целесообразность использования дисперсионной модели для описания макродисперсии в гетерогенных породах неупорядоченного строения. Численные эксперименты по массопереносу в среде с непроницаемыми включениями показали, что даже в этом идеализированном случае возникают значительные неясности в описании процесса моделью гидродисперсии, поскольку оказывается, что характер переноса мигрантов существенно зависит от расположения и масштаба включений (Лукнер, Шестаков, 1986; Мироненко, Румынин, том1, 1998). Отмечается также плохая приспособленность дисперсионной модели к описанию переноса в области ультрамалых концентраций, представляющей особый интерес при изучении переноса высокотоксичных (например, радионуклидных) мигрантов (Мироненко, Румынин, том1, 1998). получается функцией времени, причем эта функция оказывается неповторимой во всех точках наблюдений. Сомнительна также целесообразность использования дисперсионной модели для описания макродисперсии в гетерогенных породах неупорядоченного строения. Численные эксперименты по массопереносу в среде с непроницаемыми включениями показали, что даже в этом идеализированном случае возникают значительные неясности в описании процесса моделью гидродисперсии, поскольку оказывается, что характер переноса мигрантов существенно зависит от расположения и масштаба включений (Лукнер, Шестаков, 1986; Мироненко, Румынин, том1, 1998). Отмечается также плохая приспособленность дисперсионной модели к описанию переноса в области ультрамалых концентраций, представляющей особый интерес при изучении переноса высокотоксичных (например, радионуклидных) мигрантов (Мироненко, Румынин, том1, 1998).
Заметим, что при моделировании продольного конвективно-дисперсионного переноса, исходя из асимптотического его представления на основе модели гетерогенно-блоковой среды, положение переднего фронта переноса, перед которым концентрация переносимого мигранта будет нулевой, на момент времени t можно получить, как положение фронта конвективного переноса при расчетном времени t0 =(1+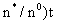 . .
2.3. Модели продольного переноса в слоистых пластах
Для водоносных пластов, сложенных осадочными породами, характерно слоистое строение, накладывающее решающее влияние на развитие процессов переноса. Рассмотрим обоснование расчетных зависимостей для переноса в слоистых пластах, выделяя условия плавной и резкой изменчивости проницаемости слоев.
Плавная изменчивость проницаемости слоев характерна для водоносных пластов, представленных сравнительно однородными песчаными отложениями. В этом случае для горизонтально-слоистых пластов в начальный период процесса продольного переноса можно использовать схему послойного переноса, в которой предполагается, что перенос в каждом слое протекает изолированно от влияния соседних слоев без учета поперечной дисперсии. Соответственно среднее (медианное) значение концентрации мигранта cm в слоистом пласте общей мощностью m, состоящем из r слоев мощностью mi каждого i-го слоя, будет
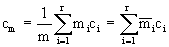 , , 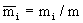 . (2.51) . (2.51)
Количество мигранта, проходящего в пласте через любое вертикальное сечение, характеризуется "выходной" концентрацией св :
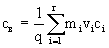 . (2.51а) . (2.51а)
где q- удельный расход потока, vi - скорость фильтрации в i-м пласте.
Поскольку величина 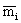 представляет собой относительную частоту встречаемости в разрезе значений действительной скорости фильтрации, то входящая в выражение (2.45) сумма является функцией распределения коэффициента конвективного переноса представляет собой относительную частоту встречаемости в разрезе значений действительной скорости фильтрации, то входящая в выражение (2.45) сумма является функцией распределения коэффициента конвективного переноса 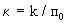 . .
А.А.Рошаль (1980) рассмотрел выражения для сm и св при нормальном и асимметричном законах распределения 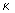 При нормальном распределении плотность распределения величины к имеет вид При нормальном распределении плотность распределения величины к имеет вид
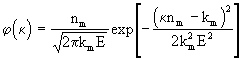 , , 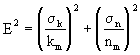 , (2.52) , (2.52)
где nm и km - средние значения активной пористости и коэффициента фильтрации, 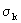 и и 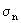 - средние квадратические отклонения k и n0. В этом случае для условий фундаментальной задачи, когда в начальной сечении - средние квадратические отклонения k и n0. В этом случае для условий фундаментальной задачи, когда в начальной сечении 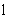 =0 одномерного потока в направлении =0 одномерного потока в направлении 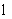 , начиная с момента времени t=0, подается мигрант с постоянной относительной концентрацией с0 = 1, средняя относительная концентрация сm представляется выражением , начиная с момента времени t=0, подается мигрант с постоянной относительной концентрацией с0 = 1, средняя относительная концентрация сm представляется выражением
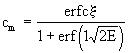 , , 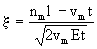 , (2.53) , (2.53)
где vm =q/m - среднее значение скорости фильтрации. Из этого уравнения следует, что время t0,5 прохождение средней относительной концентрации сm = 0,5 оказывается несколько меньше среднего времени поршневого вытеснения t0 = nm 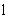 /vm , а величина /vm , а величина 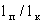 , где , где 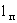 - размер переходной зоны а - размер переходной зоны а 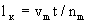 , остается постоянной во времени (при сравнительно малых значениях , остается постоянной во времени (при сравнительно малых значениях 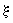 в диапазоне изменения относительной концентрации сm от 0,97 до 0,03 получается в диапазоне изменения относительной концентрации сm от 0,97 до 0,03 получается 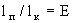 ). ).
Аналогичные решения получаются при задании коэффициента конвективного переноса некоторой алгебраической функцией (Мироненко, Румынин, том1, 1998). В частности, при линейном изменении коэффициента изменении по глубине от km -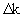 до до 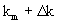 и постоянных значениях ni справедливо решение фундаментальной задачи вида (2.53) при Е = 2/3( и постоянных значениях ni справедливо решение фундаментальной задачи вида (2.53) при Е = 2/3(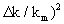 . .
Заметим, что, поскольку максимальная величина коэффициента конвективного переноса имеет конечное значение, то ею определяется конечный максимальный размер расстояния, на которое распространяется мигрант конвективным переносом в слоистом пласте.
Подходы к построению расчетных зависимостей с учетом поперечного переноса в слоистых пластах, приводящие к асимптотическом решениям для модели дисперсионного типа, приведены в работе (Мироненко, Румынин, 1998). Однако такого рода решения реально применимы лишь при очень больших временах процесса (порядка нескольких лет и более), так что предпочтительнее по-видимому проводить моделирование переноса в слоистых пластах с плавно меняющейся проницаемости при задании на модели их реальной слоистости.
Резкое различие проницаемости в слоистых водоносных пластах характерно при проводящих слоях, представленных песчаными или карбонатными породами, разделенных слоями глинистых пород. В пластах карбонатных пород роль проводящих слоев играют небольшие по мощности горизонтальные зоны повышенной трещиноватости (Лукнер, Шестаков, 1986).
Наиболее простым случаем такого типа строения пласта является двухслойный пласт, состоящий из проницаемого слоя мощностью m при пористости n и слабопроницаемого слоя мощностью 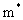 при пористости n*. В такой схеме предполагается продольный конвективный перенос в проницаемом слое и поперечный диффузионный перенос в слабопроницаемом слое, так что она соответствует схеме гетерогенно-блоковой среды, в которой каналы и блоки соответствуют проницаемому и слабопроницаемому слоям. при пористости n*. В такой схеме предполагается продольный конвективный перенос в проницаемом слое и поперечный диффузионный перенос в слабопроницаемом слое, так что она соответствует схеме гетерогенно-блоковой среды, в которой каналы и блоки соответствуют проницаемому и слабопроницаемому слоям.
В таких условиях схема ГБС 2-го типа (с неограниченной емкостью блоков) применима при условии (Лукнер, Шестаков, 1986):
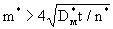 , (2.54) , (2.54)
где 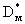 и и 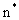 - коэффициент молекулярной диффузии и пористость пород слабопроницаемого слоя. - коэффициент молекулярной диффузии и пористость пород слабопроницаемого слоя.
Расчеты по этому условию показывают, что при мощности слабопроницаемых слоев порядка 1м схема гетерогенно-блоковой среды 2-го типа (с неограниченной емкостью блоков) имеет широкую область применения для процессов, длительностью определяемой годами. При этом расчетные зависимости в двухслойном пласте получаются заменой в приведенных выше уравнениях для ГБС 2-го типа v на q, где q-удельный расход потока , n0 на nm и при 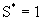 . .
Анализ фундаментального решения в этом случае показывает, в частности, что в начальный период, определяемой временем tп применима схема послойного переноса, причем можно считать (Лукнер, Шестаков, 1986; Мироненко, Румынин, том1, 1998), что
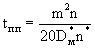 . (2.55) . (2.55)
При большем времени переноса, когда условие (2.54) не удовлетворяется, можно использовать схему ГБС 1-го типа (сосредоточенной емкости блоков). В этом случае решения задач переноса трансформируется из соответствующих решении для схемы ГБС 1-го типа с заменой в них n0 на nm, n* на n*m*, v на q при 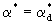 , причем, как показывает теоретический анализ, здесь можно считать , причем, как показывает теоретический анализ, здесь можно считать 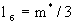 , так что для единичного элемента слабопроницаемого слоя объемом V=m* и площадью диффузионного потока , так что для единичного элемента слабопроницаемого слоя объемом V=m* и площадью диффузионного потока 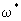 согласно (2.31а) имеем согласно (2.31а) имеем 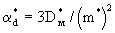 . При этом остается в силе условие с=0 при . При этом остается в силе условие с=0 при 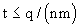 . .
Схема двухслойного пласта может непосредственно использоваться в случае квазиоднородного слоистого пласта, состоящего из N чередующихся хорошо и слабопроницаемых слоев мощностью 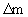 и и 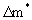 cоответственно. В этом случае используется решение для схемы двухслойного пласта которых только делаются замены q на 0,5 q/N, m на cоответственно. В этом случае используется решение для схемы двухслойного пласта которых только делаются замены q на 0,5 q/N, m на 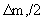 , m* на , m* на 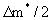 . С некоторым приближением такое решение можно применить и в случае, когда мощности слоев меняются в пределах пласта, задавая в решениях среднее значение величин мощности проводящих слоев и коэффициентов массообмена. . С некоторым приближением такое решение можно применить и в случае, когда мощности слоев меняются в пределах пласта, задавая в решениях среднее значение величин мощности проводящих слоев и коэффициентов массообмена.
Более общее решение задач переноса в слоистых пластах можно получить, проводя вычислительные модельные эксперименты по переносу в пластах с реальным профилем проницаемости для одномерного в плане потока. Сопоставляя полученные модельные данные распространения мигранта с получаемыми из решения задач по схемам ГБС, можно найти расчетные значения параметра массообмена, обеспечивающие наилучшее согласование модельных и расчетных данных.
Заметим, что поток переноса мигрантов в слоистых пластах может весьма существенно трансформироваться за счет проявления поперечного конвективного переноса, обусловленными вертикальными скоростями в фильтрационном потоке, в частности, при влиянии различия плотностей в области потока. В таких случаях для описания процессов переноса в слоистых пластах следует проводить прямое их моделирование при задании реальной слоистости водоносных пластов.
Литература к главе 2
Айдаров И.П. Регулирование водно-солевого и питательного режима орошаемых земель. 1985.
Голубев В.С. Динамика геохимических процессов. 1981.
Голубев В.С. Гарибянц А.А. Гетерогенные процессы миграции. 1968.
Лехов А.В., Соколов В.Н. Проблемы миграции продуктов разложения осадка сточных вод. //Геоэкология, N1, 2002.
Лукнер Л., Шестаков В.М. Моделирование миграции подземных вод. 1986.
Манукьян Д.А., Штенгелов Р.С. Особенности миграции подземных вод при крупном водоотборе //Вестник МГУ, серия геол., N6, 1972.
Мироненко В. А., Румынин В.Г., Проблемы гидрогеоэкологии,том1,1998; том 3.1999.
Орадовская А.Е. Миграция вещества и тепла в подземных водах. //Гидрогеологические исследования за рубежом. 1982.
Письмен П.М., Кучанов С.И., Левич В.С. Поперечная диффузия в зернистом слое. Доклады АНСССР, т.174, N3, 1967.
Рошаль А.А.Методы определения миграционных параметров // Обзор ВИЭМС.
Гидрогеология и инж. геол. 1980.
Тютюнова Ф.И. Гидрогеохимия техногенеза. 1987.
Чеверев В.Г. Природа криогенных свойств грунтов. 2004.
Шестаков В.М. Гидрогеодинамика. 1995.
|


