|
Перчук Алексей Леонидович
Автореферат диссертации на соискание ученой степени доктора геолого-минералогических наук
|
содержание |
В первой части главы рассматриваются минеральные равновесия, которые использовались для восстановления Р-Т условий метаморфизма, описывается специфика исследований, проводимых на микрозонде, и в заключении излагаются методические основы минеральной хронометрии.
Геотермобарометрия
Основное внимание в разделе уделено минеральному равновесию
альбит = жадеит + кварц, (1.1)
на котором базируется клинопироксен - плагиоклаз - кварцевый геобарометр. Геобарометр может использоваться в широком интервале температур и давлений, охватывающих условия эклогитовой, глаукофановой, амфиболитовой и гранулитовой фаций метаморфизма. Краевая система (NAS, Na20-Al2O3-SiO2) реакции (1.1) изучена настолько добротно (Newton, Smith, 1967; Holland, 1980), что используется для калибровки экспериментальных установок типа цилиндр-поршень. В более сложной системе (МСNАS: MgO-СаО-Na20-Al2O3-SiO2) экспериментально определены составы равновесных с альбитом и кварцем пироксенов ряда Jd-Di (Kushiro, 1968; Bell, Kalb, 1969; Holland, 1983; Gasparik, 1985). Энтальпия смешения этого твердого раствора изучалась с помощью калориметрии (Wood et al. 1980). Значительный вклад в энергию смешения твердого раствора Di-Jd вносит упорядочение, обусловленное фазовым переходом C2/c P2/n (Clark, Papike, 1966). В последующих исследованиях (Сarpenter, 1979; Wood et al., 1980; Carpenter, 1981, 1983; Holland, 1983; Rossi et al., 1983; Davidson, Burton, 1987; Rossi, 1988; Сarpenter et al., 1990; Holland, 1990; Vinograd, 2002) был установлен общий вид фазовой диаграммы, а также определены энтальпия и свободная энергия упорядочения омфацита. Общее описание свойств Jd-Di твердого раствора с использованием разных термодинамических моделей содержится во многих публикациях (Gasparik, 1985; Сohen, 1986; Kurepin, 1983; Burton, Davidson, 1988 а,б; Holland, 1990; Holland, Powell, 1996; Mayre et al., 1997; Nakamura, Banno, 1997; Vinograd, 2002 а, б). Однако термодинамическое моделирование твердого раствора Jd-Hd, и, как следствие, тройного раствора Jd-Hd-Di началось с результатов наших экспериментальных и теоретических исследований (Аранович, Перчук, 1989; Перчук, Аранович, 1991; Перчук, 1992). P2/n (Clark, Papike, 1966). В последующих исследованиях (Сarpenter, 1979; Wood et al., 1980; Carpenter, 1981, 1983; Holland, 1983; Rossi et al., 1983; Davidson, Burton, 1987; Rossi, 1988; Сarpenter et al., 1990; Holland, 1990; Vinograd, 2002) был установлен общий вид фазовой диаграммы, а также определены энтальпия и свободная энергия упорядочения омфацита. Общее описание свойств Jd-Di твердого раствора с использованием разных термодинамических моделей содержится во многих публикациях (Gasparik, 1985; Сohen, 1986; Kurepin, 1983; Burton, Davidson, 1988 а,б; Holland, 1990; Holland, Powell, 1996; Mayre et al., 1997; Nakamura, Banno, 1997; Vinograd, 2002 а, б). Однако термодинамическое моделирование твердого раствора Jd-Hd, и, как следствие, тройного раствора Jd-Hd-Di началось с результатов наших экспериментальных и теоретических исследований (Аранович, Перчук, 1989; Перчук, Аранович, 1991; Перчук, 1992).
Геденбергит - жадеитовый твердый раствор
Эксперимент. Смесимость в твердом растворе Hd-Jd оценивались с помощью реакции 1.1 по растворимости жадеита в геденбергите в присутствии альбита и кварца в диапазоне температуры 900-1100o С и давления 14-25 кбар. Эксперименты проводились на установке цилиндр-поршень. В качестве исходных веществ использовалось (1) смесь природного кварца, низкого альбита и синтетического геденбергита или (2) смесь природного кварца с омфацитом (Hd40Jd60) в соотношении 2:3 соответственно. В первом случае геденбергит выращивался в течение 7 дней в гидротермальных условиях при 700o С, 1 кбар в присутствии 0.2 М раствора СaCl2.
В прямых опытах (смесь 1) предполагалось, что равновесным составом обладает омфацит с предельным содержанием жадеита. В обратных опытах (смесь 2), в качестве равновесного принимался состав клинопироксена с минимальным количеством жадеитовой молекулы. Химический состав продуктов опытов изучался с помощью микрозонда. Результаты экспериментов обрабатывались термодинамически.
Термодинамика. С учетом фазового перехода  Qtz = Qtz = 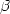 Qtz (Mirwald, Massone, 1980) свободная энергия Гиббса реакции (1.1) имеет вид (Gasparik, 1985) Qtz (Mirwald, Massone, 1980) свободная энергия Гиббса реакции (1.1) имеет вид (Gasparik, 1985)
9360 - 44T + (1.827 - 31*10-7 P) P + RT ln ( aJd / aAb) = 0. (1.2)
Свойства смешения в ряду Jd-Hd рассчитаны посредством молекулярной (однопозиционной) модели
aJd = 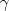 Jd xJd . (1.3) Jd xJd . (1.3)
и уравнения субрегулярного раствора
GJde = RT ln 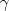 Jd = AG (2 x3 - x2 ) + BG (2 x2 - 2 x3 ), (1.4) Jd = AG (2 x3 - x2 ) + BG (2 x2 - 2 x3 ), (1.4)
где x= xHd ; AG = AH - T AS. Параметры взаимодействия AH = 670  150; AS = 9.0 150; AS = 9.0  0.4; BH = 15090 0.4; BH = 15090  630; BS = 8.0 630; BS = 8.0  0.3 в (1.4) рассчитывались методом наименьших квадратов. В результате термодинамической обработки результатов экспериментов была обнаружена знакопеременная концентрационная зависимость избыточной интегральной молярной свободной энергии Гиббса. 0.3 в (1.4) рассчитывались методом наименьших квадратов. В результате термодинамической обработки результатов экспериментов была обнаружена знакопеременная концентрационная зависимость избыточной интегральной молярной свободной энергии Гиббса. Диопсид - жадеитовый твердый раствор
Термодинамичекие свойства Di-Jd твердого раствора рассчитывались по такой же методике, как и для Hd-Jd твердого раствора. Только в этом случае использовались литературные данные по равновесию (1.1) в присутствии диопсида (Holland, 1983; Gasparik, 1985). Вводилась также поправка на упорядочение (переход C2/c P2/n) в омфаците, приходящееся на довольно широкую Р-Т область природного минералообразования. При описании избыточной энергии Гиббса для омфацита в твердом растворе Di-Jd использовались молекулярная модель (1.3) и уравнение субрегулярного раствора (1.4). Расчетные параметры взаимодействия AH = 16570 P2/n) в омфаците, приходящееся на довольно широкую Р-Т область природного минералообразования. При описании избыточной энергии Гиббса для омфацита в твердом растворе Di-Jd использовались молекулярная модель (1.3) и уравнение субрегулярного раствора (1.4). Расчетные параметры взаимодействия AH = 16570  2120; AS = 13.5 2120; AS = 13.5  1.7; BH = 13270 1.7; BH = 13270  1670; BS = 9.3 1670; BS = 9.3  1.2 в уравнении (1.4) позволяют с высокой степенью точности описать экспериментальные данные (рис.1.2). Выражение концентрационной зависимости интегральной энтальпии смешения для твердого раствора Jd-Di 1.2 в уравнении (1.4) позволяют с высокой степенью точности описать экспериментальные данные (рис.1.2). Выражение концентрационной зависимости интегральной энтальпии смешения для твердого раствора Jd-Di
He = xJd xDi (AH xDi + BH xJd )
неплохо согласуется с термохимическими данными (Wood et al, 1980) в редакции Р.Коэна (Cohen, 1986).
Упорядочение, связанное с фазовым переходом C2c P2/n в твердом растворе Jd-Di, оказывает существенное влияние на его термодинамические свойства. Парциальная энергия упорядочения жадеита, в рамках теории Ландау, имеет следующее выражение (Holland, 1990; Перчук, 1992) P2/n в твердом растворе Jd-Di, оказывает существенное влияние на его термодинамические свойства. Парциальная энергия упорядочения жадеита, в рамках теории Ландау, имеет следующее выражение (Holland, 1990; Перчук, 1992)
GJdord= -а/3 [4XDi (1-XDi)Tc -T)/Tc]1/2 (2Tc XDi (4XDi -1)-T), (1.5)
где Tc =1138 K, а=11.3 Дж/моль/К.
Тройной твердый раствор жадеит-геденбергит-диопсид
Интегральное выражение избыточной свободной энергии жадеита в тройном растворе Jd-Di-Hd при идеальном смешении в ряду Di-Hd (Berman, 1990) имеет вид:
GeJd = RT ln 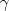 Jd = G(1) + G(2) + G(3)+ (1- 2xJd ) xHdxDi C, (1.6) Jd = G(1) + G(2) + G(3)+ (1- 2xJd ) xHdxDi C, (1.6)
где G(1) = ХMg GJdord , G(2) = АG12 (2XHd3 - XHd2 ) + 2 BG13 (XHd2 - XHd3 ), G(3) = АG13 (2XDi3 - XDi2 ) + 2 BG13 (XDi2 - XDi3 , AG12 = 3679 - 9T, BG12 = 15090 - 8T, АG13 = 16570 - 13.5T, BG13 = 13270-9.3T, ХMg = Mg/(Mg+Fe). Параметр упорядочения вводится только для омфацитов ряда Jd-Di, где этот эффект был установлен экспериментально (Сarpenter, 1981). Твердый раствор плагиоклаза
Для описания избыточной свободной энергии смешения альбита использовалось уравнение субрегулярного раствора (Perchuk et al., 1991)
GeAb = (1- xAb)2 [(28675 - 16.19T ) - 2xAb (20398 - 9.81 T )] ,
где xAb= Na/(Na+Ca). В дополнении к этому вводились эффекты, связанные с переходами моноклинный-триклинный (Тс = 1251 К) и высокий-низкий альбит (Тс = 833 К). Энергетическая составляющая этих эффектов рассчитывается по выражению (Salje et al, 1985)
GordAb = F ord + P V ord ,
в котором V ord = 0.036 Дж/бар, отвечает переходу высокий  низкий альбит, низкий альбит,
Ford = ½ a0 (T-Tc*) Q 2 + ¼ b Q 4 + ½ aod0 (T-Tcod*) Qod2 + ¼ bod Q 4 + 1/6 cod Qod6 + (d0 + 2 d1T + 3 d1T 3 ) Q Qod , Q = -1.9*10-6 T 2 + 2.1*10-3 T + 0.3795; Qod = -0.012*10-3 T + 1.5127; Tc = 1251 K, Tcod = 824.1 K, a0, b, aod0, bod, cod, d0, d1 , d2 и d3 - константы (Salje et al, 1985).
Таким образом, выражение для полной избыточной энергии альбита
GeхAb = GeAb + ХAb G ordAb (1.7)
имеет две составляющие - избыточную энергию смешения альбита в твердом растворе плагиоклаза и энергию его упорядочения.
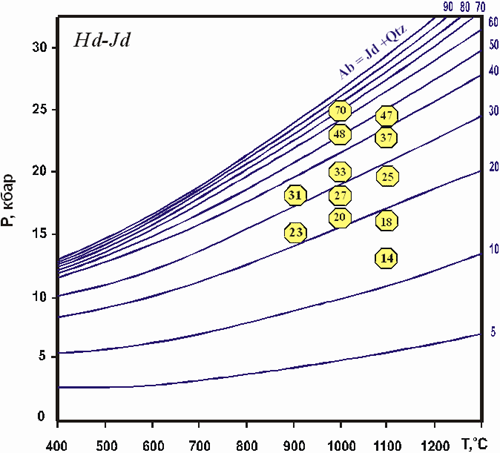 |
| Рис.1.1. Р-Т диаграмма Сpx-Pl-Qtz барометра в железистой системе. Изоплеты - расчетные значения XJd в твердом Jd-Hd растворе. Цифры в кружках - равновесные XJdCpx по экспериментальным данным (Перчук, 1992). |
Уравнение клинопироксен-плагиоклаз-кварцевого барометра
Окончательное уравнение геобарометра, учитывающего структурные состояния клинопироксена и альбита, получается подстановкой (1.3), (1.6) и (1.7) в (1.2)
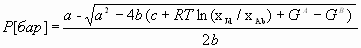 , (1.8) , (1.8)
где а = 1.827+0.036 хAb Qod Дж/бар, b = 3.1*10-6 Дж/бар2 , c = 44T -9360, GA = GJde , GB = GAbe +XAbG ord . Точность геобарометра составляет около 2 кбар (Перчук, 1992).
На рис. 1.1 и 1.2 представлена графическая версия геобарометра. Экспериментальные точки, вынесенные на диаграммы, позволяют судить о степени согласования предлагаемого барометра с экспериментальными данными. Изоплеты в низкотемпературной области выполаживаются - это связано с упорядочением в альбите. На Р-Т диаграмме для магнезиальной системы (рис.1.2) показана область
 |
|
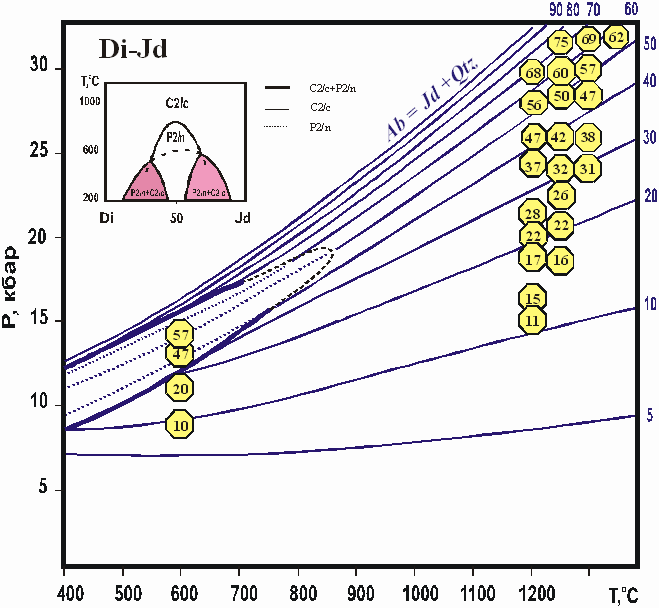
Рис.1.2. Р-Т диаграмма для Сpx-Pl-Qtz барометра в магнезиальной системе. Изоплеты XJd в твердом Jd-Di растворе. Цифры в кружках: равновесные XJdCpx в экспериментах (Gasparik, 1985; Holland, 1983). Жирная линия оконтуривает область упорядочения (Р2/n). На врезке показана фазовая Т-ХJd диаграмма для Jd-Di клинопироксенов (Rossi et al 1983).
|
упорядочения омфацита, в которой часть изоплет (например, Jd30 и Jd70) отвечают метастабильному состоянию омфацита из-за распада твердого раствора. При наличии в плагиоклазе анортитовой молекулы изоплеты смещаются в область более высокого давления. При отсутствии в породе плагиоклаза барометр показывает минимальное давление. Минеральная хронометрия
Минеральной хронометрия (геоспидометрия) как метод восстановления скоростей термальной истории породы по степени диффузионного изменения состава минерала(ов) имеет два направления, в основе которых лежит: 1) диффузионный обмен между сосуществующими минералами и 2) обмена компонентами между гранатом и внешней средой. . Гетерофазный обмен
Это направление минеральной хронометрии (и метод в целом) приобрело широкую известность благодаря теоретическим разработкам (Lasaga et al, 1977, Lasaga, 1979, 1983), которые впоследствии успешно применялись к природным объектам (Герасимов, 1992; Lundstrem, 1992; Герасимов, Савко, 1996; Ganguly et al, 2000). В рамках данного подхода температурная эволюция породы устанавливается по диффузионной зональности, которая возникает на границе двух контактирующих минералов за счет неравновесного протекания обменных реакций в условиях регрессивной температурной эволюции. Надо отметить, что данный метод оказался не достаточно эффективным при исследованиях эклогитов ввиду отсутствия катионного обмена между сосуществующими минералами (Перчук и др, 1996; Aranovich, Pattison, 1995). Объемная диффузия в изолированном кристалле
Движущей силой процесса в данном случае является градиент концентрации химических элементов, формируемый при росте кристаллов. С.Чакраборти и Д. Гангули (Chakraborty, Ganguly, 1991) заключили, что данное направление, представленное к тому времени лишь несколькими исследованиями (Anderson, Olimpio, 1977; Walker et al., 1977; Yardley, 1977; Muncill, Chamberain, 1988), не имеет перспектив в геологии из-за (1) сложности восстановления исходной ростовой зональности в кристаллах; и (2) привноса-выноса компонентов в гранат в ходе метаморфизма, т.е. невыполнение условия закрытой системы.
Знаковой работой в области развития данного метода стала работа Жианга и Ласаги (Jiang, Lasaga, 1990), в которой содержится теоретический анализ безразмерной переменной t'
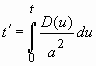 , (1.9) , (1.9)
где u - переменная интегрирования, t время, a - радиус кристалла, D - коэффициент диффузии, представленный уравнением Аррениуса
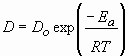 , (1.10) , (1.10)
в котором Do - предэкспоненциальный фактор, Ea - энергия активации, зависящая от давления, R - универсальная газовая постоянная, T - температура. Авторы показали, что выражение (1.9) позволяет исследовать любые термальные истории.
При исследовании термальной истории пород некоторые исследователи (Muncill, Chamberain, 1988) используют выражение А. Ласаги (Lasaga, 1983) T = Т0 / (1 + st / T0), где Т0 - температура начала неравновесного массообмена, s - скорость остывания. Другие же (Ganguly et al 1996; O'Brien, Vrana, 1995; Dachs, Proyer, 2002) для неизотермической задачи вводят характеристическую температуру ТCh ~0.97*TPeak (Chakraborty, Ganguly, 1991), где TPeak - температура пика метаморфизма в градусах Кельвина. Эта процедура существенно упрощает решение задачи, но является довольно грубым изотермическим приближением.
Концентрическая ростовая зональность и ее гомогенизация
Это наиболее распространенный тип зональности метаморфических гранатов. В зависимости от снабжения растущих граней кристалла минералообразующим веществом зональность может быть непрерывной или прерывистой.
Для описания эволюции исходного профиля в изотропном сферическом кристалле радиуса а можно использовать уравнение диффузии в сфере
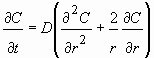 , (1.11) , (1.11)
где С - концентрация диффундирующего компонента, r - радиальная позиция.
Ниже приводятся частные решения этой диффузионной задачи при граничных условиях закрытой системы.
Для случая прерывистого роста, следствием которого является скачкообразное изменение состава граната (Rosenfeld, 1970; Rumble, Finnerty, 1974; Tracy, 1982; Перчук и др. 1998), гомогенизация зонального профиля может быть представлена выражением (напр. Перчук и др. 1998)
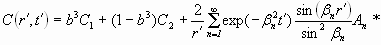
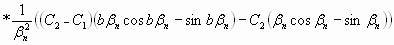 , (1.12) , (1.12)
где b = h/a, h - граница между ядром и каймой, а - радиус, С1 и С2 - начальное распределение диффундирующего компонента в ядре и кайме, соответственно.
Непрерывный рост граната приводит к появлению множества зональных форм. Способы математического описания и моделирования некоторых из них приводятся в работе (Perchuk, Philippot, 2000). Например, профиль, описываемый тригонометрической функцией
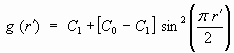 , ,
где C0 и C1 - содержание диффундирующего компонента в ядре и кайме, соответственно, преображается за счет диффузии следующим образом:
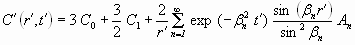 , ,
где
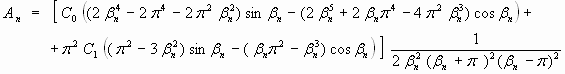
Гомогенизация изолированного сферического кристалла с зональным профилем линейного вида g(r,0) = a + b r' , где a и b - константы, описываться выражением
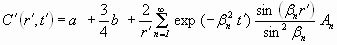 , ,
где 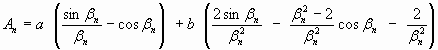
При наличии высокоградиентных участков в краевой зоне граната (глава 2) может быть использована полиномиальная функция:
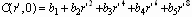
где bi - константы. В этом случае уравнение гомогенизации будет следующим:
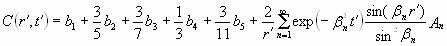 , (1.13) , (1.13)
где 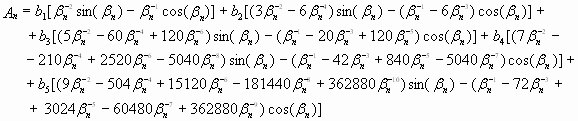
Гомогенизация в тонком слое (диффузия в бесконечной тонкой пластине)
Иногда в гранатах встречаются стрингеры (главы 2-4) - тонкие жильные участки химической гетерогенности, возникающие в результате залечивания микротрещин (Перчук, Варламов, 1995). Для описания гомогенизации стрингера целесообразно рассматривать задачу о диффузии из протяженной пластины ограниченной мощности в бесконечном пространстве (Lasaga, 1998).
Выражение, описывающее изменение состава стрингера и вмещающего граната:
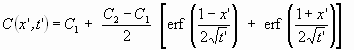 , (1.14) , (1.14)
в котором С1 - содержание компонента вне стрингера, С2 - в стрингере, t' - безразмерная переменная (ур-е 1.9), где вместо радиуса используется половина мощности стрингера, erf - функция ошибок вида
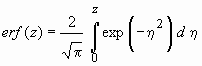 , где , где 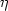 - переменная интегрирования. - переменная интегрирования.
Полубесконечная диффузионная пара
Эта одномерная задача о диффузии между минералами контрастного состава, имеющими плоскую границу раздела. Решение этой задачи часто используется для экспериментального изучения объемной диффузии в минералах (Loomis et al., 1985; Герасимов, 1989; Chakraborty, Ganguly, 1992; Ganguly et al, 1998; Demianov, 1999), но может применяться также при исследованиях природных кристаллов большого радиуса, для которых можно пренебречь влиянием кривизны границы между зонами роста (Ganguly et al., 1996; Перчук и др., 1998; Глава 5). Аналитическое решение этой задачи (Crank, 1975):
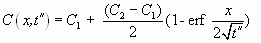 (1.15) (1.15)
где 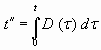 , С1 и С2 - исходные содержания диффундирующего компонента по обе стороны от границы раздела, причем С1 - минимальное содержание компонента. , С1 и С2 - исходные содержания диффундирующего компонента по обе стороны от границы раздела, причем С1 - минимальное содержание компонента.
Основной подход
Нижеизложенная методика позволяет восстанавливать скорости изменения температуры и давления в течение метаморфической эволюции пород, включающей прогрессивный и регрессивный этапы метаморфизма, производить мониторинг Р-Т условий прекращения эффективного массопереноса, когда наступает остановка геохронометра.
Суть методики состоит в поиске термальной и барической истории кристалла, которая отвечала бы значению переменной t' (ур-е 1.9), характеризующей степень гомогенизации исходной ростовой зональности (Перчук и др. 1996, 1998; Perchuk, Philippot, 1997, 2000; Перчук, 2002). Рассмотрим случай линейного охлаждения и подъема сферического зонального кристалла известного радиуса (рис.1.3а). На начальной стадии установим значение переменной t'h, которое показывает степень сглаживания (гомогенизации) исходной ростовой зональности. Для этого используем одну из вышеизложенных диффузионных задач, позволяющую адекватно описать характер зональности граната и ее диффузионную релаксацию. Далее вычислим интеграл (1.9), т.е. определим переменную t' для кристалла известного размера при заданных параметрах охлаждения (To(Ро) Tlim(Рlim)). Каждая термальная и барическая история (связь Р и Т определяется Р-Т трендом метаморфизма) имеет собственную кривую зависимости переменной t' от текущего значения времени (рис.1.3а). Tlim(Рlim)). Каждая термальная и барическая история (связь Р и Т определяется Р-Т трендом метаморфизма) имеет собственную кривую зависимости переменной t' от текущего значения времени (рис.1.3а).
Совокупность точек, отвечающих T=Tlim для разных термальных историй, образует прямую линию.
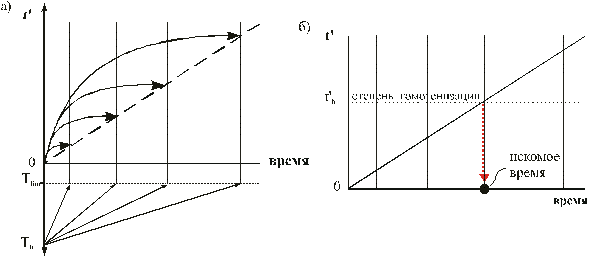 |
| Рис.1.3. а) Схематический вид зависимости переменной (t') от текущего значения времени (ур-е 1.9) при различных скоростях линейного охлаждения кристалла известного радиуса с постоянными начальной (Т0) и конечной (Тlim) температурами. Каждой термальной истории (T-t координаты) соответствует одна кривая в координатах t'-время. (б) Графический способ определения длительности процесса по известной степени гомогенизации граната t'h. |
Искомое решение дает та термальная история, переменная t', которой соответствует степени гомогенизации (t'h) граната (рис.1.3б).
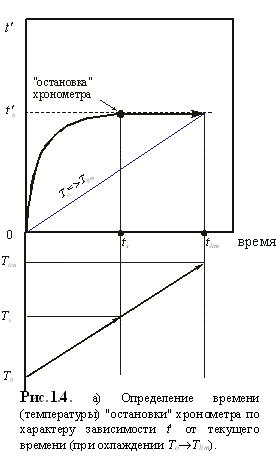
Для оценки фактической температуры (давления, времени) прекращения эффективного массопереноса в минерале следует рассчитывать изменение переменной t' в ходе термальной эволюции. На рис.1.4 схематично показано, как устанавливаются ts и Ts остановки хронометра. Скорости изменения давления оцениваются с учетом функциональной зависимости давления от температуры, представленной в виде Р-Т тренда.
Основными источниками ошибок метода являются оценки температуры и коэффициенты диффузии катионов (Gangluly et al., 1995; Perchuk, Philippot, 1997; Dachs, Proyer, 2002).
Многокомпонентная диффузия: численные решения и новая программа
При многокомпонентном потоке диффундирующих компонентов в неизотермических условиях целесообразно пользоваться численным решением. С этой целью была создана программа XXL, которая позволяет моделировать многокомпонентную диффузию для сферических и декартовых координат при любой форме зависимости Т и Р от времени. Программа учитывает зависимость коэффициента диффузии от состава и может использоваться для любого типа зонального профиля. Программа работает в электронной таблице Microsoft EXCEL, существенно облегчающей ее использование и графическое представление результатов.
При многокомпонентной диффузии поток каждого катиона в минерале зависит от линейной комбинации градиентов остальных катионов с линейными коэффициентами, заданными матрицей коэффициентов диффузии Dij. В случае зависимости коэффициентов диффузии (Dij) от состава соотношение Фика-Онзагера (Onsager, 1945) имеет следующий вид
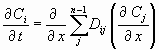 , (1.16) , (1.16)
где Ci мольная доля компонента в n-компонентной системе, x - расстояние.
Диффузионная матрица (D) в ионных кристаллах рассчитывается по выражению (Lasaga, 1979):
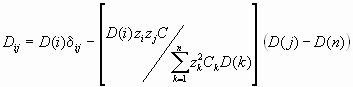 , (1.17) , (1.17)
где 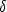 ij = 0 при i ij = 0 при i 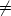 j и j и 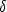 ij =1 при i=j, z - заряд компонента, компонент n рассматривается как зависимый. Коэффициент самодиффузии D(i) компонента i описывается уравнением (1.10). ij =1 при i=j, z - заряд компонента, компонент n рассматривается как зависимый. Коэффициент самодиффузии D(i) компонента i описывается уравнением (1.10).
При моделировании использовался метод консервативных конечных разностей на нерегулярной сетке. Разностные схемы записывались в неявной форме на основе интегро-интерполяционного метода (Калиткин, 1978). Системы уравнений решались с помощью метода исключений Гаусса. Следуя сложившейся практике (Loomis et al., 1985), для тестирования программы применялось аналитическое решение задачи о диффузии между двумя полубесконечными средами, с коэффициентами диффузии, линейно зависящими от состава (Crank, 1975, стр.118). Сопоставление численного и аналитического решения для случая сильной зависимости коэффициента диффузии от состава (Crank 1975, с. 386, табл. 7.5, b=0.1407) показывает хорошую сходимость результатов (Перчук, Геря, 2004, в печати).
| Полные данные о работе |
Геологический факультет МГУ |
|


