|
Владов Михаил Львович
Автореферат диссертации на соискание ученой степени доктора физико-математических наук
|
оглавление |
Содержание работы.
Введение.
Во введении обосновывается актуальность темы диссертационной работы, сформулирована цель и задачи исследований.
Глава 1. Исторический очерк. Физические основы метода.
Интерес к волнам давления в трубах, заполненных жидкостью, имеет давнюю историю и охватывает широкие сферы человеческой деятельности, которые включают в себя, например, такие далекие друг от друга области как техника водоснабжения, робототехника с гибкими гидравлическими связями, скважинная геофизика, гидродинамика кровотока с пульсовой диагностикой.
Далее, в каждой области возникают свои специфические условия - какая именно труба рассматривается, ее размеры, свойства стенок, свойства окружающего пространства, свойства заполняющей жидкости, параметры и режим работы источника волн и т.д. Несмотря на это, поскольку интерес к
волнам в трубах в разных областях возникал не одновременно, практически до настоящего времени ученые не оставляют попыток создать максимально общую теорию этого явления.
В первой главе проведено рассмотрение исторически сложившихся взглядов на распространение волн давления в трубах, применительно к ситуации в водонаполненной скважине и выделение той области существующих теоретических построений, которую можно использовать для дальнейшего извлечения геолого-геофизической информации из результатов натурных наблюдений.
Рассмотрение явления передачи давления в скважинах как в трубах, в том числе, с бесконечно толстыми упругими стенками и рассмотрение этого процесса как специфической волны, существующей благодаря наличию контакта "жидкость-твердое тело", определили первую точку ветвления теории - принципиально два разных направления описания явления. Развитие первого направления связано с именами Рэлея, Лэмба и Жуковского Н.Е. Основоположниками второго, волнового направления являются Стоунли и Био.
В результате решения статической задачи Лэмбом получено выражение для скорости распространения волны давления в трубе с бесконечно толстыми стенками (прямой аналог скважины в массиве пород). Скорость определяется свойствами заполняющей скважину жидкости и, что самое важное для скважинных исследований, сдвиговой характеристикой околоскважинного пространства:
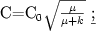
где 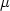 -модуль сдвига бесконечно толстой стенки трубы (околоскважинного пространства), k - модуль объемной упругости жидкости, -модуль сдвига бесконечно толстой стенки трубы (околоскважинного пространства), k - модуль объемной упругости жидкости,
k =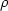 0 С02, 0 С02, 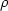 0 - плотность жидкости, С0 - скорость звука в жидкости. 0 - плотность жидкости, С0 - скорость звука в жидкости.
Жуковским Н.Е. получено выражение для скорости распространения гидроудара в трубах:
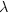 =( =(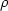 0/k + 2 0/k + 2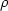 0R0/eE)-1/2, 0R0/eE)-1/2,
где 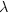 - скорость распространения ударной волны; - скорость распространения ударной волны;
k- сжимаемость жидкости;
R0 - внутренний радиус трубы;
е- толщина стенок трубы;
Е - модуль Юнга стенок трубы;
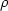 0 - плотность жидкости. 0 - плотность жидкости.
Для развития того или иного теоретического направления ключевым вопросом будет соотношение длин волн и диаметра скважины, поскольку в пределе 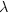 /d /d  0 задача сводится к теории волн Стоунли, а на противоположном конце оси 0 задача сводится к теории волн Стоунли, а на противоположном конце оси 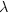 /d /d  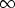 - к чисто статическому "трубному" случаю. - к чисто статическому "трубному" случаю.
Классической теорией по высокочастотным гидроволнам являются работы Био. В них исследовано влияние аксиальной симметрии на волны Стоунли, исходя из волнового уравнения для потенциала смещения в жидкости в цилиндрических координатах:
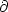 2 2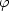 / /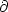 r2+1/r r2+1/r 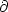 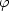 / /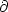 r + r + 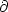 2 2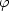 / /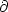 z2 = 1/C2 z2 = 1/C2 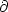 2 2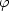 / /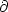 t2 , t2 ,
где С -скорость упругих волн в неограниченной жидкости;
r - радиальная координата;
z- вертикальная координата, направленная по оси скважины.
Решение для случая гидроволн - волн давления в заполняющей скважину жидкости, которые Био называет волнами Стоунли, было записано в виде :
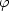 = I0[r(l2 - = I0[r(l2 -  2/C2)] ei(lz- 2/C2)] ei(lz- t) t)
при условии  2/C2 < l2 , 2/C2 < l2 ,
где I0 - модифицированная функция Бесселя первого рода нулевого порядка;
 - круговая частота - круговая частота  = 2 = 2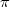 f; f;
l - волновое число, l =  /v; /v;
v - фазовая скорость гидроволны.
В случае увеличения частоты фазовая скорость гидроволн стремится к значению скорости волн Стоунли для плоской границы "жидкость-твердое полупространство", зато с уменьшением частоты фазовая скорость гидроволн стремится к горизонтальной ассимптоте, определяемой выражением:
V = C0/(1+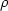 0C02/ 0C02/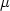 )1/2 )1/2
Это выражение соответствует приведенным ранее результатам Лэмба и Н.Е. Жуковского.
Таким образом, классическая статическая теория и низкочастотная асимптотика, развитая Био указывают на возможность использования, по крайней мере, кинематических характеристик гидроволн - волн давления - для изучения сдвиговых характеристик околоскважинного пространства.
В современной литературе волны давления в скважине называют по-разному - в акустическом каротаже волнами Лэмба, в других случаях трубными волнами и гидроволнами. В данной работе предпочтение отдано обобщающему термину "гидроволна" как правило с указанием "высокочастотная" или "низкочастотная", определяющим характер ее образования и распространения.
В диссертации проведен анализ современных теоретических разработок и экспериментальных результатов по использованию гидроволн в широком частотном диапазоне от акустического каротажа (АК) до низкочастотных вариантов при вертикальном сейсмическом профилировании (ВСП) и работах в неглубоких водонаполненных скважинах (НВС) с источниками типа центра расширения. Наиболее развита теория высокочастотных гидроволн в АК, однако и здесь ряд экспериментальных фактов противоречат теоретическим представлениям. Кроме того, в данной работе определен ряд существенных отличий ситуации при акустическом каротаже с длинами волн сущеcтвенно меньшими диаметра скважины и ситуации при решении задач изучения верхней части разреза.
- Соотношение длин волн и диаметров скважин - в АК длины волн составляют первые сантиметры, а диаметры скважин первые десятки сантиметров, в то время как в НВС длины волн доходят до десятка метров, а диаметры скважин редко превышают 127 мм.
- Заполняющая скважину жидкость в АК, как правило, представляет собой специальный раствор, акустические свойства которого, существенно отличаются от свойств воды, характерной для ситуации в НВС.
- Источники колебаний в АК, как правило, пъезоэлектрического типа, маломощные и "задавленные" большим гидростатическим давлением, в то время как в НВС это малолитражные пневмоисточники (до 0,5 литра) и электроискровые источники с энергиями до первых килоджоулей, создающие значительные поршневые эффекты в скважине вплоть до выбросов воды.
Необходимо отметить, что имеющиеся в литературе теоретические расчеты сделаны в предположении характерных для сейсмического и акустического подходов предположения о слабых воздействиях и малых смещениях частиц в среде в дальней (волновой) зоне.
- Среда в случае АК значительно более высокоскоростная по отношению к заполняющей скважину жидкости, а в верхней части разреза, зоне малых скоростей, характерна прямо противоположная ситуация, что и затрудняет применение АК в приповерхностных частях разреза. Это определяет, например, характер гидроволн как излучающихся в массив, затухающих, характеризующих приствольную часть скважины, по крайней мере в несколько ее диаметров в отличие от ситуации АК.
- Удаления "источник - приемник" в АК составляют первые метры, а при решении задач в НВС это могут быть многие десятки метров. Соответственно с этим расширяются возможности изучения поглощения волн разных типов, дисперсионного анализа и т.д.
- В АК принципиально источник и приемник размещены в одной скважине, тогда как при исследовании в НВС чрезвычайно актуальны задачи межскважинных просвечиваний, просвечиваний типа "поверхность - скважина". Отсюда возникает совершенно новая теоретическая задача о волновом поле в скважине при внешнем возбуждении различными источниками.
- В отличие от случая АК, где направление "источник - приемник" строго фиксировано вдоль оси скважины, при исследовании НВС по методикам различных просвечиваний, возникают вопросы о характеристиках направленности источников и приемных устройств с точки зрения динамики волн разных типов.
Все эти вопросы вызвали ряд теоретических и экспериментальных исследований, посвященных распространению именно низкочастотных волн в скважине и окружающем ее массиве пород.
Наиболее полное и последовательное теоретическое описание процесса возбуждения и распространения волн в скважинах с жидкостью и вмещающем массиве пород можно найти в работах Дж. Уайта. Достигнутые им результаты позволяют пытаться решать задачи значительно более приближенные к условиям скважин в приповерхностной части разреза, хотя некоторые фундаментальные выводы аналогичны уже приведенным результатам Лэмба и Н.Е. Жуковского.
Для скважины, внутри которой расположен источник типа центра расширения, Дж. Уайт рассмотрел поршневое движение в жидкости, зависящее только от одной координаты Z и времени t - давление p(z,t) и смещение uz (z,t). Получено волновое уравнение для гидроволн в виде:
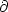 2uz/ 2uz/ 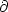 z2 = 1/ Gт2 z2 = 1/ Gт2 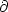 2uz/ 2uz/ 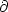 t2 , t2 ,
где Gт= [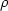 0(1/ B + 1/ 0(1/ B + 1/ 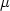 )]-1/2 - скорость распространения гидроволн (трубных, tube waves по терминологии Дж. Уайта); )]-1/2 - скорость распространения гидроволн (трубных, tube waves по терминологии Дж. Уайта);
B - объемный модуль жидкости;
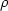 0 - плотность жидкости; 0 - плотность жидкости;
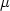 - модуль сдвига вмещающих пород. - модуль сдвига вмещающих пород.
Решения волнового уравнения предcтавляют собой две волны, бегущих от точки возбуждения в противоположных направлениях со скоростью Vг (в нашей терминологии) гидроволны:
uz = f(t - z/ Vг); uz = f(t + z/ Vг).
Давление в скважине в любой момент определяется формулой:
p(z,t) = 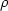 0 Vг f 0 Vг f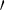 t(t t(t  z/ Vг). z/ Vг).
Уайт рассмотрел общий случай, когда изменяются скачком свойства массива (горизонтальная граница), диаметр скважины и свойства заполняющей скважину жидкости. Им получены выражения для коэффициентов отражения гидроволн от границ слоев, пересекаемых скважиной, изучены вопросы затухания гидроволн вследствие поглощения и излучения энергии, рассмотрены вопросы образования обменных гидроволн при падении прямых продольных волн на границы раздела сред с различными сдвиговыми свойствами, вопросы дисперсии гидроволн и изменения характеристик гидроволны вблизи проницаемой зоны.
Однако, экспериментальные исследования, как показано в диссертации, количественно не подтверждают многие теоретические положения. Это касается в первую очередь вопросов частотной зависимости коэффициентов отражения гидроволн, зависимости характеристик гидроволн от амплитуды возбуждаемого импульса давления, соотношения динамически характеристик волн разных типов в реальных средах. Кроме того, ключевым и нерешенным вопросом является вопрос о функции источника и возможности управлять параметрами функции источника.
Выводы.
Проведенный анализ теорий возбуждения и распространения упругих волн в наполненных жидкостью трубах и скважинах показывает:
- теоретически получены решения волновых уравнений для высокочастотных (по отношению к диаметру скважины) гидроволн и как асимптотический переход - низкочастотных волн давления;
- формальный асимптотический переход от высоких частот к низким подтверждает только связь скорости гидроволн с модулем сдвига околоскважинного пространства;
- низкочастотная теория поршневого движения предсказывает появление нескольких типов вторичных волн давления, связанных с особенностями разреза.
Обзор экспериментальных работ и собственный опыт показывают:
1. результаты наблюдений в реальных средах не подтверждают многие количественные положения теории;
2. наименее изученным является диапазон между соотношениями длин волн и диаметров скважин 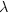 /d << 1 и /d << 1 и 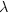 /d > 1, то есть по частотам, между первыми сотнями герц и первыми килогерцами; /d > 1, то есть по частотам, между первыми сотнями герц и первыми килогерцами;
3.предсказаны теорией, но не изучены и не используются в решениях практических задач вторичные волны давления совместно с прямыми продольными волнами и гидроволнами.
Для реализации теоретических и экспериментальных предпосылок исследования верхней части разреза путем комплексного изучения волн давления в скважине наиболее эффективно использование бесконтактных источника типа центра расширения и приемников давления - устройств, не требующих прижима к стенке скважины.
Возможность управления частотным составом и интенсивностью возбуждаемых колебаний при малых размерах излучателей, реализованная в открытой воде для электроискрового источника создает предпосылки для использования этого источника при изучении верхней части разреза в скважинах.
Рассмотренные в первой главе вопросы определяют основное содержание работы, которая направлена на повышение эффективности сейсмических методов при изучении верхней части разреза.
| Полные данные о работе |
Геологический факультет МГУ |
|


