 |
|
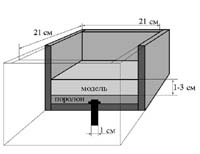
Рис. 37. Устройство, использованное в моделировании в первой и второй серии опытов.
|
Модель. Прибор, использованный в моделировании, представляет собой деревянный ящик с размерами 21х21х8 см (рис. 37), в который снизу может вдвигаться цилиндрический штамп диаметром 1 см. Для придания жесткому штампу куполообразной формы, схожей с верхней частью мантийного диапира, на дне ящика находилась пластина поролона толщиной 0.5 см. Поверх нее закладывался слой модельного материала - песка или глины. Маркеры на поверхность моделей не наносились из-за технических трудностей их нанесения на песчаные модели. Высота поднятия штампа составляла примерно 2-2.5 см.
Модельный слой представлял собой параллелепипед, квадратный в плане, со сторонами 21х21 см и с меняющейся мощностью в разных опытах: от 1 до 3 см (рис. 37). Полученные в процессе моделирования деформации - неоднородные, т.е. поле напряжений для всей модели в целом неоднородно. Они фиксируются на поверхности модели в виде нарушений сплошности модели, по которым возможна оценка величины деформации. Изменяя мощность модельного слоя, выяснялась зависимость рисунка деформаций от соотношения размеров: диаметр штампа - мощность модели. То есть это модель изменения соотношений поперечника диапира и мощности перекрывающих его образований
Ход эксперимента. Моделирование проводилось при комнатной температуре. Поднятие штампа происходило на протяжении 30 с. В ходе эксперимента нами фотографировались в плане: 1) картина деформаций модельного слоя после поднятии штампа; 2) картина деформаций модельного слоя после возвращении штампа в исходное положение.
Первая серия опытов.
Опыт 1. Материал: песок с солидолом. Мощность модели 1 см.
 |
|
Рис. 38. Первая серия опытов. Пояснения в тексте.
|
Первая стадия - штамп поднят (рис. 38): Высота поднятия штампа составила 1.9 см. На поверхности модели образуется изометричный в плане купол с зоной перегиба склона у его подножия. Средний радиус купола (по 24 измерениям) составил 68.0 мм (табл. 8). Стандартное отклонение величины радиуса 6.4 мм. Измерение сделано по концентрическим трещинам второй стадии опыта (см. ниже). По периферии поднявшегося купола, на его склонах вплоть до подножия, возникает радиальная структура трещиноватости (А). Происходит открытие зияющих трещин, свидетельствующих о расширении поверхности модели. При этом, чем ближе к центральной части купола, тем больше величина раскрытия трещин (до 2-2.5 мм). К периферии купола, т. е. к его подножию, трещины постепенно сужаются, сходя на нет у границы купола и не выходя за нее. Эта система трещиноватости свидетельствует о концентрическом растяжении в пределах купола.
Ближе к центральной части купола радиальная система трещиноватости сменяется сегментированной концентрической (В), представляющей собой также систему трещин растяжения, но уже кольцевую (вокруг центральной части поднятия). Величина раскрытия трещин данной системы до 2.5-3.5 мм. Эта система является переходной к следующей, центральной зоне и, по сути, является ее граничной частью.
Центральная часть купола диаметром около 5.5 см имеет блоково-полигональное строение (С). При этом наблюдается зависимость величины блоков от их местоположения. Их средние размеры изменяются от крыльев поднятия, где они составляют в среднем 1х1 см, к его центру, где они уменьшаются до 2х2 мм. Наличие эта зоны свидетельствует о всестороннем растяжении, как концентрическом, так и радиальном в центральной части купола. Таким образом, на этой стадии визуально наблюдается лишь деформация растяжения.
Для более наглядного представления о величине деформаций нами была замерена дилатация модели по площади. В нашем случае дилатация является выражением хрупкой составляющей полной величины деформации. Нами измерялось процентное увеличение площади поверхности модели за счет зияния трещин. Пластичную составляющую из-за отсутствия маркеров мы оценить не могли. Измерения проводились в пределах квадратного окна со стороной 6.5 мм. Результаты замеров были обработаны методом скользящего среднего с окном 13 х 13 мм. Это дает нам представление о распределении усредненной величины дилатации на поверхности. Мы наблюдаем довольно изометричную в плане картину распределения дилатации по площади купола с отдельными аппендиксами по наиболее раскрывшимся зонам трещиноватости (С, В, и Ю-З в относительных координатах) (рис. 38). Максимальная дилатация (40%) наблюдается в виде области концентрической формы по восточному краю центральной зоны. На снимках эта область соответствует наиболее раскрытым зонам трещиноватости.
Вторая стадия - возвращение штампа в исходное положение (рис. 38): При возвращении штампа в исходное состояние куполообразное поднятие перестает существовать. Все системы трещиноватости растяжения предыдущей стадии опыта практически полностью закрываются (D). Остаются лишь следы, преимущественно концентрической системы (зияние до 1.5 мм). Радиальная система закрывается практически полностью, но кое-где остаются ее следы (ширина до 0.5 мм). Большинство из них концентрируется в С-В части от центра образца (в условных координатах). Закрытие на второй стадии трещин растяжения, образованных на первой стадии, свидетельствует об обстановке сжатия.
 |
|
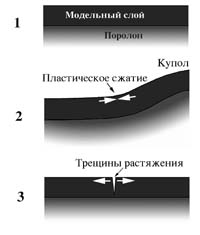
Рис. 39. Механизм образования концентрических трещин растяжения на второй стадии опытов с песком.
|
По границе бывшего купола возникает новая система трещиноватости (E), представляющая собой концентрические, почти кольцевые разрывы. Механически они подобны трещинам раскрытия первой стадии опыта. Очевидно, при опускании купола произошло возвращение склонов купола на исходную горизонтальную поверхность, а следовательно, распрямление изгиба модели в основании склона. Вследствие распрямления этого изгиба и некоторой хрупкости материала модели и возникла данная система концентрической трещиноватости (рис. 39). Этот изгиб у подножия склона купола из первоначально горизонтального положения на первой стадии опыта должен был сопровождаться поверхностным радиальным сжатием. Очевидно, что эта обстановка радиального сжатия действительно существовала на первой стадии опыта, хотя ее следы, да и то косвенные, мы можем наблюдать только на второй стадии. Принимая данную систему трещин, возникшую в зоне максимального перегиба модельного слоя, за границы купола на первой стадии опыта, мы можем измерить диаметр купола по его подножию.
Для представления о степени развития концентрической трещиноватости, образованной на второй стадии, нами были измерены величины зияний радиальных трещин в 24 направлениях (с шагом 15o). Из них на одном из этих направлений трещины не были встречены. Нас интересовала величина раскрытия данной системы трещин и радиус купола (рис. 38). Среднее раскрытие трещин (концентрическая система трещин второй стадии опыта): 0.5 мм. Стандартное отклонение - 0.3 мм. Закрывающуюся на данном этапе радиальную систему трещин мы не измеряли.
Из сказанного следует, что и на первой, и на второй стадии одновременно существовали условия сжатия и растяжения. На первой стадии в центре были условия растяжения, на периферии - сжатия. На второй стадии произошла инверсия напряжений: в центре условия сжатия, на периферии - растяжения.
Мы также попытались приблизительно определить форму купола, сравнивая прирост площади поверхности (в процентах) при воздымании купола по результатам измерения дилатации с теоретическим расчетом прироста в двух идеальных случаях: поднятие в форме конуса и в форме сегмента шара (табл. 9). Оказалось, что в данном опыте прирост поверхности модели занимает промежуточное положение между двумя теоретическими случаями - между конусом и сегментом шара, но все же ближе к сегменту шара.
Опыт 2. Материал: песок с солидолом. Мощность модели 2 см.
Первая стадия - штамп поднят (рис. 38): Высота поднятия штампа: 2.0 см. На поверхности модели возникает изометричный в плане купол с зоной перегиба у его подножия. Средний радиус купола составил 69.2 мм, стандартное отклонение - 6.4 мм (оценка по концентрическим трещинам второй стадии). По периферии поднятого купола мы можем наблюдать систему раскрывшихся радиальных трещин растяжения (A). По мере продвижения к центру купола эти трещины расширяются до 3.5-3.9 мм, ближе к периферии купола трещины сокращаются и постепенно у границы купола исчезают. Эта система трещиноватости свидетельствует о концентрическом растяжении в пределах купола.
К центру картина деформаций приобретает блоково-полигональный характер (C). В отличие от опыта 1 в данном опыте нет переходной концентрической составляющей системы растяжения вокруг центральной части. Размеры блоков не изменяются в зависимости от местоположения. Они примерно одинакового размера (около 0.9 см в поперечнике) и формы (близкой к изометричной). Диаметр центральной блоково-полигональной зоны составляет около 4.5 см. Наличие этой зоны свидетельствует о всестороннем растяжении, как концентрическом, так и радиальном в центральной части купола. Видимый характер деформаций - исключительно деформации растяжения. При удалении от центра степень деформации (величина зияния) уменьшается. В целом характер деформаций аналогичен таковому в предыдущем опыте, за исключением картины трещиноватости в центральной части купола.
При замерах дилатации таким же методом, как и ранее (скользящего среднего), мы получили картину, несколько отличающуюся от предыдущей (рис. 38). Она менее изометрична в плане, сильнее выражены аппендиксы, соответствующие на снимках зонам наибольшего раскрытия трещин растяжения. Зона максимальной дилатации находится на С-В (в условных координатах) центральной части купола. Максимум дилатации достигает 40%.
Вторая стадия - возвращение штампа в исходное положение (рис. 38): При опускании штампа наблюдается картина, аналогичная второй стадии предыдущего опыта. Структуры растяжения первой стадии почти полностью закрываются (D), оставляя зияния не более 1 мм. Большинство трещин закрывается целиком. Следы не закрывшихся трещин группируются к В - С-В от центра модели. Вероятно, неполное закрытие большинства трещин и зияние некоторых из них можно объяснить несимметричной просадкой купола при опускании штампа. Скорее всего, это вызвано неоднородностями в приборе, вероятно, в слое поролона.
Так же как и ранее (опыт 1) на этой стадии мы наблюдаем новообразованную концентрическую систему трещин растяжения (E). По сравнению с опытом 1 она менее развита. Трещины менее раскрыты и представляют собой не почти непрерывную кольцевую структуру, а лишь отдельные, хотя и протяженные фрагменты ее. Трещины не встречаются в 5 направлениях из 24. Данная система трещин маркирует стадию локального радиального сжатия по периферии купола в первой стадии опыта. Среднее раскрытие трещин (концентрическая система трещин второй стадии опыта): 0.2 мм, стандартное отклонение - 0.2 мм (табл. 8).
По сравнению с опытом 1 форма купола изменилась. Значения прироста поверхности очень близки к таковым для случая конуса (табл. 9).
Опыт 3. Материал: песок с солидолом. Мощность модели 3 см.
Первая стадия - штамп поднят (рис. 38): Высота поднятия штампа: 2.0 см. На поверхности модели образуется изометричный в плане купол с зоной перегиба склона у его подножия. Средний радиус купола составил 66.2 мм, стандартное отклонение - 6.0 мм (оценка по концентрическим трещинам второй стадии). При воздымании купола возникает радиальная система трещин растяжения (A). На флангах купола трещины сужаются и сходят на нет, а ближе к центру раскрываются до 3.8-4 мм, сходясь в единый узел и образуя в самом центре провал на поверхности размерами около 0.9 х 1.3 см. Данная система трещиноватости свидетельствует о концентрическом растяжении в пределах купола. В центральной части наблюдается эмбриональная блоковая зона. Наличие данной зоны свидетельствует о всестороннем растяжении, как концентрическом, так и радиальном в центре купола. Видимый характер деформаций - растяжение. Общая картина деформаций такая же, как и в более ранних опытах.
При оценке дилатации методом скользящего среднего мы получаем картину так же неизометричную, как и в опыте 2, с хорошо выраженными аппендиксами (рис. 38), определяемыми зонами хорошо развитой трещиноватости, и с максимумом дилатации в центральной части купола (более 60%). Максимум дилатации соответствует провалу в центре купола на снимке.
Вторая стадия - возвращение штампа в исходное положение (рис. 38). Опуская штамп, мы повторяем условия предыдущих опытов; повторяется и принципиальная картина деформаций. Трещиноватость растяжения первой стадии закрывается (D), оставляя зияния лишь на С-В от центра модели (величина зияния до 1-1.3 мм). Объясняется это, как уже говорилось, неравномерным опусканием купола. Концентрическая система трещиноватости растяжения проявлена еще слабее, нежели в опыте 2 (E). Она представляет собой фрагменты кольцевой структуры. Раскрытие данной системы еще слабее, чем в опыте 2 (рис. 38). Трещины не встречаются в 9 направлениях из 24. Тем не менее по этим фрагментам все же возможно определить диаметр купола на предыдущей стадии развития модели. Среднее раскрытие трещин (концентрическая система трещин второй стадии опыта): 0.2 мм. Стандартное отклонение - 0.2 мм (табл. 8).
Судя по измеренной величине дилатации на первой стадии опыта 3, форма купола близка к конусообразной (табл. 9). В целом, характер деформаций в опыте 3 тот же, что и в опытах 1 и 2.
|


