|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
XII.3. Преобразование координат точек (атомов), индексов ребер кристалла - узловых рядов
Переход от координат точек в старой исходной координатной системе к координатам этих же точек в новой системе удобно рассмотреть графически, обратившись к рис. 209. Если некоторая точка (узел) К с координатами mnp в старой координатной системе имеет в новой координаты MNP, то вектор 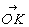 , идущий из начала координат в точку К, можно выразить как векторную сумму старых или новых единичных векторов: , идущий из начала координат в точку К, можно выразить как векторную сумму старых или новых единичных векторов:
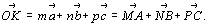 (7) (7)
Обратившись к системе уравнений, где векторы старой координатной системы представлены как векторные суммы новой:
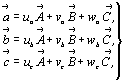 (8) (8)
и подставив значения векторов 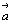 , , 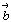 , , 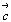 в уравнение (7), получим в уравнение (7), получим
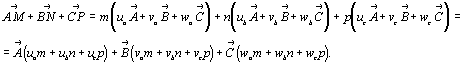
Отсюда следует, что
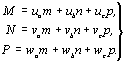
Оказалось, что матрица, отражающая прямое преобразование координат точек в старой координатной системе к координатам этих же точек в новой системе 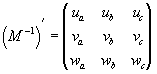 , не что иное, как транспонированная обратная матрица , не что иное, как транспонированная обратная матрица 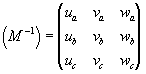 , т.е. матрица, в которой строки и столбцы поменялись местами. Такой закон преобразования называется контравариантным. , т.е. матрица, в которой строки и столбцы поменялись местами. Такой закон преобразования называется контравариантным.
Таким образом, для получения координат точки в новом репере следует одностолбцовую матрицу из ее старых координат умножить на обратную транспонированную матрицу (М- 1)' :
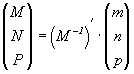 1. 1.
Обратившись к рис. 209, увидим, что координаты точки К в старой координатной системе m = 4, n = 6, p = 0. Для вычисления координат MNP этой точки в новой системе следует матрицу не прямого, а обратного преобразования от новой координатной системы к старой 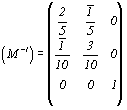 транспонировать: транспонировать: 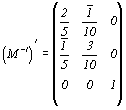 и, умножив одностолбцовую матрицу из старых координат на обратную транспонированную матрицу, рассчитать их значения: и, умножив одностолбцовую матрицу из старых координат на обратную транспонированную матрицу, рассчитать их значения:
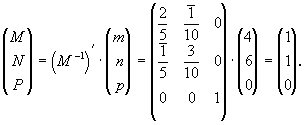
Очевидно, что для обратного преобразования координат точек (от новых к старым) следует пользоваться транспонированной прямой матрицей (М)' :
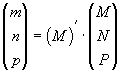 . .
Контравариантный закон справедлив и для преобразования символов ребер кристаллов, ибо их индексы r, s, t не что иное, как относительные координаты m, n, p точки расположенной на ребре. Таким образом, для перехода от символа некоторого ребра [rst], рассчитанного в старой координатной системе, к символу этого же ребра [RST] в новой системе следует, как и при определении координат точек, выразить вектор от начала координат до точки, взятой на этом ребре, как векторные суммы старых и новых единичных векторов:
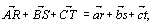
и, воспользовавшись системой уравнений (8), по вышеприведенной схеме составить матрицу преобразования индексов ребер:
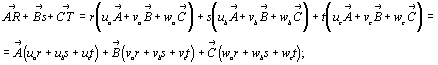
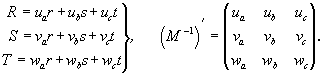
И далее получить искомый результат:
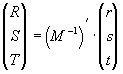 и и 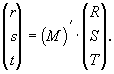
В итоге, используя ковариантный или контравариантный закон преобразования координатных осей, плоскостей, ребер, координат точек и т.п., можно решить многие практические кристаллографические задачи. Однако при их решении следует помнить, что символы каких-либо направлений - ребер, координатных осей, а также плоскостей - граней или атомных сеток - представляют собой отношения целых взаимно простых чисел. Поэтому, когда мы говорим, что строки матриц прямого (М) и обратного (М- 1) преобразований выражают символы новых координатных осей в старой системе координат либо, наоборот, старых - в новой, следует иметь в виду, что в качестве индексов могут оказаться и дробные числа. И для того, чтобы получить миллеровские стандартные символы указанных осей (символы из целочисленных индексов), следует исключить из них общий множитель (n). Так, обратная матрица (М-1)нов.--> стар. в приведенном на с. 356 примере в качестве своих членов содержит дроби:

В первой строке этой матрицы записаны координаты ближайшего к началу координат узла (точки), расположенного на старой координатной оси X, отношения которых соответствуют символу старой оси X в новой координатной системе: 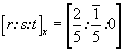 . После изъятия общего множителя n1=1/5 стандартная запись этого символа будет . После изъятия общего множителя n1=1/5 стандартная запись этого символа будет 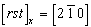 . Вторая строка матрицы соответствует символу старой оси Y: . Вторая строка матрицы соответствует символу старой оси Y: 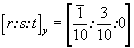 ; ; 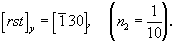 Третья строка матрицы указывает в данном случае на неизменность оси Z: Третья строка матрицы указывает в данном случае на неизменность оси Z: 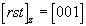 . Однако умножение матрицы прямого преобразования - для нашего случая . Однако умножение матрицы прямого преобразования - для нашего случая 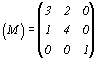 на обратную матрицу, составленную из "приглаженных" индексов на обратную матрицу, составленную из "приглаженных" индексов 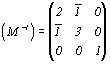 , не даст, как ожидалось (см. с. 356), единичную матрицу: , не даст, как ожидалось (см. с. 356), единичную матрицу:
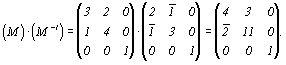
И лишь введение в обратную матрицу изъятых при получении символов осей общих множителей n1 и n2 даст ожидаемый результат: 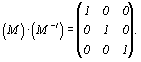
Поэтому, решая конкретные задачи, например составляя матрицу преобразования осей:
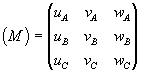
по известным "приглаженным" символам [r1 s1 t1 ], [r2 s2 t2 ] и [r3 s3 t3 ] новых координатных осей X' , Y' и Z' соответственно, следует для каждого из них ввести общий множитель (n), в общем случае n 1: 1:
uA : vA : wA = r1 : s1 : t1 = n1r1 : n1s1 : n1t1 = [r1s1t1],
uB : vB : wB = r2 : s2 : t2 = n2r2 : n2s2 : n2t2 = [r2s2t2],
uC : vC : wC = r3 : s3 : t3 = n3r3 : n3s3 : n3t3 = [r3s3t3].
В результате матрица, составленная по старым символам новых координатных осей с учетом общих множителей, будет иметь следующий вид:
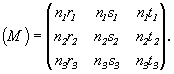
Для определения общих множителей (n) следует воспользоваться соотношениями символов некоторой грани (плоскости), рассчитанных в старой (hkl) и новой (HKL) координатных системах.
Воспользовавшись уравнением (6), запишем:
H = uAh+vAk+wAl = n1r1h + n1s1k + n1t1l = n1(r1h + s1k + t1l).
Отсюда 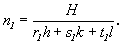 (9) (9)
Аналогично могут быть получены значения и остальных общих множителей: 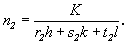 и и 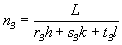 [28 ]. [28 ].
Однако и в этом случае при определении значений общих множителей (n1,n2,n3) следует пользоваться не приглаженными символами (HKL) исходной грани, а символами, содержащими общий множитель (p): (E . p F . p G . p), где H = E . p, K = F . p, L = G . p. В противном случае будет получен неверный результат. Так, каждая строка матрицы прямого перехода от старой координатной системы к новой (см. с. 354) 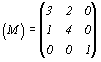 представляет символ соответствующей новой координатной оси в старой системе: X' = [320], Y' = [140], Z' = [001]. В данном случае общие множители в символах всех осей равны 1. Если же общие множители неизвестны, то они могут быть найдены из соотношения старого (hkl) и нового (HKL) символов некоторой грани. Пусть старый символ (hkl) некоторой грани будет (212). Найдем ее новый символ, воспользовавшись матрицей прямого преобразования (см. (2) ): представляет символ соответствующей новой координатной оси в старой системе: X' = [320], Y' = [140], Z' = [001]. В данном случае общие множители в символах всех осей равны 1. Если же общие множители неизвестны, то они могут быть найдены из соотношения старого (hkl) и нового (HKL) символов некоторой грани. Пусть старый символ (hkl) некоторой грани будет (212). Найдем ее новый символ, воспользовавшись матрицей прямого преобразования (см. (2) ):
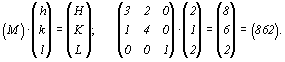
Полученный символ содержит общий множитель p = 2, на который обычно и сокращают индексы символа грани. Таким образом, окончательный символ исходной грани будет (431). Далее, пользуясь формулами (9), можно рассчитать значения общих множителей n . Однако, для того чтобы получить верный результат, в указанную формулу следует подставлять не сокращенные индексы (431), а индексы, содержащие общий множитель p, т.е. (862). Поэтому, оперируя символами граней, нужно быть уверенным, что индексы их символов содержат этот общий множитель (p):
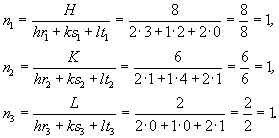
Геологический факультет МГУ
|


