|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.6. Вывод пространственных групп тетрагональной сингонии
Если в пространственных группах ромбо-бипирамидального класса mmm плоскости всех трех позиций символа топологически одинакoвы, хотя и независимы, то в группах тетрагональной голоэдрии 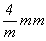 наличие одной оси 4-го порядка, всегда ориентированной вдоль вертикальной координатной оси Z, делает горизонтальную плоскость (теперь уже 1-й позиции символа) топологически отличной от вертикальных плоскостей. Кроме того, топологически различными оказываются вертикальные координатные и диагональные плоскости ввиду их различной ориентировки по отношению к координатным трансляциям элементарной ячейки - наличие одной оси 4-го порядка, всегда ориентированной вдоль вертикальной координатной оси Z, делает горизонтальную плоскость (теперь уже 1-й позиции символа) топологически отличной от вертикальных плоскостей. Кроме того, топологически различными оказываются вертикальные координатные и диагональные плоскости ввиду их различной ориентировки по отношению к координатным трансляциям элементарной ячейки - 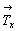 и и 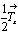 . .
Эквивалентность горизонтальных координатных особых направлений в тетрагональных группах обусловлена не только поворотом на 90o вокруг всегда присутствующей оси 4-го порядка, но и существованием диагональных особых направлений, расположенных к координатным под углом 45o . При этом ось 4-го порядка можно считать порожденной взаимодействием координатных и диагональных элементов симметрии.
Таким образом, естественен переход от групп ромбической сингонии к их тетрагональным надгруппам с диагональными особыми направлениями. Введение равнонаклонных к координатным особым направлениям исходных ромбических групп либо диагональных плоскостей симметрии (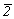 = md), либо поворотных осей симметрии 2-го порядка (2d) не только автоматически делает координатные направления X и Y эквивалентными, но и повышает порядок вертикальной оси от 2 до 4, т.е. тетрагонализирует ромбические группы по схеме (рис. 82) = md), либо поворотных осей симметрии 2-го порядка (2d) не только автоматически делает координатные направления X и Y эквивалентными, но и повышает порядок вертикальной оси от 2 до 4, т.е. тетрагонализирует ромбические группы по схеме (рис. 82)
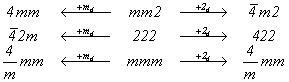
Остальные геми- и тетартоэдрические тетрагональные пространственные группы, подчиненные точечным 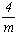 , , 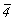 и 4, легко выводятся в качестве подгрупп более высокосимметричных тетрагональных групп. и 4, легко выводятся в качестве подгрупп более высокосимметричных тетрагональных групп.
Вывод пространственных групп тетрагональной голоэдрии на основе пространственных групп ромбической сингонии
В голоэдрических пространственных группах тетрагональной сингонии порождающими удобно считать плоскости симметрии всех трех позиций символа (двух координатных и одной диагональной) и при выводе в качестве исходных подгрупп использовать полученные ранее пространственные группы ромбической голоэдрии, расширение - тетрагонализацию - которых можно осуществить введением диагонального особого направления, представленного либо нормалью к плоскости симметрии (т.е. осью 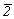 ), либо поворотной осью 2-го порядка, на третью - диагональную - позицию символа. Однако для получения тетрагональных пространственных групп класса ), либо поворотной осью 2-го порядка, на третью - диагональную - позицию символа. Однако для получения тетрагональных пространственных групп класса 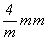 основой могут послужить лишь те пространственные группы класса mmm, в которых плоскости симметрии на 1-й и 2-й позициях ромбического символа однотипны: основой могут послужить лишь те пространственные группы класса mmm, в которых плоскости симметрии на 1-й и 2-й позициях ромбического символа однотипны:
Pmmm, Pccm, Pnnm, Pbam, Pmmn, Pccn,
Pnnn, Pban, Pmma, Pcca, Pnna,
Cmmm, Cmma, Cccm, Ccca,
Immm, Ibam, Imma,
Fmmm, Fddd.
Очевидно, что тетрагонализация ромбических групп с С- и F-решеткой Браве приведет к Р- и I-тетрагональным группам соответственно (см. с. 92).
Прежде чем начать вывод голоэдрических групп тетрагональной сингонии, следует выяснить, какие типы плоскостей возможны в качестве диагональных, т.е. на 3-й позиции тетрагонального символа. Взаимодействия координатных трансляционных векторов решетки (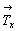 и и 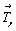 ) с косо расположенными к ним диагональными плоскостями симметрии обусловят появление новых плоскостей - плоскостей с иным типом трансляционных компонент. Разложив каждый из координатных векторов на две составляющие ( ) с косо расположенными к ним диагональными плоскостями симметрии обусловят появление новых плоскостей - плоскостей с иным типом трансляционных компонент. Разложив каждый из координатных векторов на две составляющие (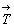 = =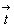 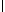 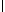 + + 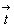  ) (рис. 83, а, б), одна из которых ( ) (рис. 83, а, б), одна из которых (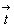 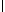 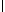 ) параллельна диагональной плоскости, а другая ( ) параллельна диагональной плоскости, а другая (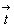  ) перпендикулярна ей, увидим, что первая, влившись в исходный элемент симметрии, создаст производную плоскость скользящего отражения с иной трансляционной компонентой, вторая - перпендикулярная составляющая - перенесет эту плоскость параллельно на половину своей длины (см. с. 50). В результате возникнет чередование диагональных плоскостей m(b) и с(n): ) перпендикулярна ей, увидим, что первая, влившись в исходный элемент симметрии, создаст производную плоскость скользящего отражения с иной трансляционной компонентой, вторая - перпендикулярная составляющая - перенесет эту плоскость параллельно на половину своей длины (см. с. 50). В результате возникнет чередование диагональных плоскостей m(b) и с(n):
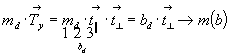 (рис. 83, а), (рис. 83, а),
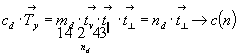 (рис. 83, б), (рис. 83, б),
что естественно сократит количество выводимых классов вдвое 1.
Пространственные группы с Р-решеткой
Введение одной (из двух возможных на диагональном направлении) независимой плоскости - m(b) или c(n) - в каждую из восьми приведенных выше ромбических пространственных групп с Р-решеткой (групп с горизонтальной плоскостью m или n) удвоит их количество. При этом результирующая ось 4-го порядка будет поворотной, если каждая из исходных вертикальных плоскостей (координатная и диагональная) имеет вертикальную трансляционную компоненту 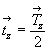 или обе плоскости будут без них. Если же вектор или обе плоскости будут без них. Если же вектор 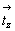 содержится лишь в одной из взаимодействующих плоскостей, то возникнет винтовая ось 42: содержится лишь в одной из взаимодействующих плоскостей, то возникнет винтовая ось 42:
| Тетрагональная пр. группа |
Ромбическая пр. группа |
Тетрагональная пр. группа |
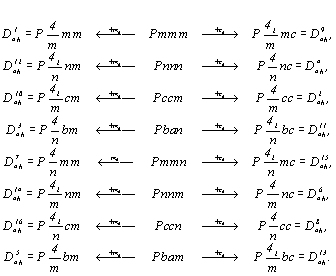 |
Тетрагонализация оставшихся трех ромбических групп с горизонтальной плоскостью а - Pmma, Pnna, Pcca - приведет, как и в предыдущем случае, к появлению осей 4 или 42. При этом горизонтальная плоскость а, будучи повернутой любой из возникших осей 4-го порядка (4 или 42) на 90o , превратится в плоскость b на этом же уровне вдоль оси Z (рис. 84). Наличие двух взаимно перпендикулярных векторов 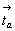 и и 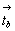 - трансляционных составляющих плоскостей а и b - создаст дополнительный суммарный реальный вектор - трансляционных составляющих плоскостей а и b - создаст дополнительный суммарный реальный вектор 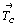 = = 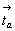 + + 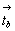 , направленный в центр горизонтальной грани элемен-тарной ячейки, т.е. приведет к базоцентрированной тетраго-нальной решетке Браве, а следовательно, к возможности выбора Р-ячейки вдвое меньшего объема. В такой новой тетрагональной Р-ячейке исходные трансляционные составляющие , направленный в центр горизонтальной грани элемен-тарной ячейки, т.е. приведет к базоцентрированной тетраго-нальной решетке Браве, а следовательно, к возможности выбора Р-ячейки вдвое меньшего объема. В такой новой тетрагональной Р-ячейке исходные трансляционные составляющие 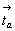 и и 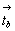 окажутся ориентированными по диагоналям ее базиса, т.е. станут трансляционными компонентами клиноплоскости n, перпендикулярной главной оси (рис. 84), а координатные плоскости исходных ромбических групп станут диагональными с соответствующими (за счет взаимодействия с координатными трансляциями новой ячейки) чередованиями: m(b) и c(n). Это объединит две ромбические группы Рcca и Рnna в одну тетрагональную - окажутся ориентированными по диагоналям ее базиса, т.е. станут трансляционными компонентами клиноплоскости n, перпендикулярной главной оси (рис. 84), а координатные плоскости исходных ромбических групп станут диагональными с соответствующими (за счет взаимодействия с координатными трансляциями новой ячейки) чередованиями: m(b) и c(n). Это объединит две ромбические группы Рcca и Рnna в одну тетрагональную - 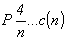 . Заданные же тетрагонализирующие диагональные плоскости m и с в новой ячейке станут координатными. При этом горизонтальные трансляционные составляющие чередующихся с ними плоскостей b и n окажутся равными координатным трансляциям новой Р-ячейки, т.е. указанные плоскости превратятся в плоскости m и с соответственно. В результате тетрагонализация указанных групп ромбической голоэдрии с плоскостями а на 3-й позиции символа к новым тетрагональным группам не приведет: . Заданные же тетрагонализирующие диагональные плоскости m и с в новой ячейке станут координатными. При этом горизонтальные трансляционные составляющие чередующихся с ними плоскостей b и n окажутся равными координатным трансляциям новой Р-ячейки, т.е. указанные плоскости превратятся в плоскости m и с соответственно. В результате тетрагонализация указанных групп ромбической голоэдрии с плоскостями а на 3-й позиции символа к новым тетрагональным группам не приведет:
| Тетрагональные пр. группы |
Ромбические пр. группы |
Тетрагональные пр. группы |
| в Р-аспекте |
в С-аспекте |
в С-аспекте |
в Р-аспекте |
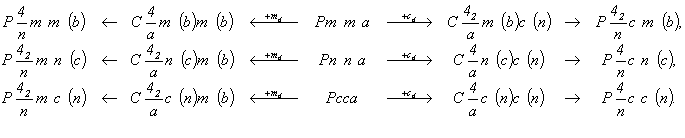 |
Не получим новых пространственных групп и в результате тетрагонализации указанных выше групп ромбической голоэдрии с С-решеткой, ибо возможность выбора в каждой из них тетрагональной Р-ячейки даст одну из 16 уже выведенных пространственных групп:
| Тетрагональные пр. группы |
Ромбические пр. группы |
Тетрагональные пр. группы |
| в Р-аспекте |
в С-аспекте |
в С-аспекте |
в Р-аспекте |
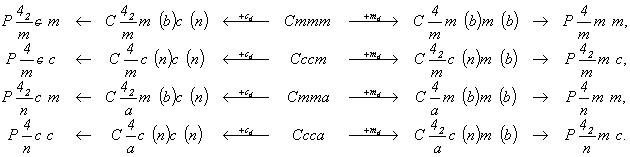 |
Все голоэдрические группы с Р-решеткой можно получить и простым перебором плоскостей на трех позициях тетрагонального символа: формальное задание плоскостей четырех типов (a, b, c, n) на 2-й (координатной) позиции символа даст 4 варианта пространственных групп, двух типов плоскостей (m(b) или c(n)) - на 3-й (диагональной) позиции удвоит их количество (4 . 2 = 8) и, наконец, задание двух типов плоскостей (m или n) на 1-й (горизонтальной) позиции символа приведет к 16 искомым пространственным группам (8 . 2 = 16). Однако при таком "прямом", достаточно механическом выводе теряется порой столь полезная связь между пространственными группами ромбической и тетрагональной сингоний.
Пространственные группы с I-решеткой
В тетрагональных пространственных группах с I-решеткой наличие дополнительного вектора 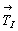 , центрирующего объем ячейки и лежащего в диагональном ее сечении, приводит к тому, что, во-первых, диагональные плоскости не только чередуются - m(b), c(n), но и каждая из них при этом одновременно выполняет две функции: плоскость m оказывается тождественно равной клиноплоскости n, а плоскость b - плоскости с: m , центрирующего объем ячейки и лежащего в диагональном ее сечении, приводит к тому, что, во-первых, диагональные плоскости не только чередуются - m(b), c(n), но и каждая из них при этом одновременно выполняет две функции: плоскость m оказывается тождественно равной клиноплоскости n, а плоскость b - плоскости с: m  n (b n (b  c); во-вторых, появляется возможность существования диагональной "алмазной" клиноплоскости d, ибо сечение (110) в I-ячейке центриро вано (!). c); во-вторых, появляется возможность существования диагональной "алмазной" клиноплоскости d, ибо сечение (110) в I-ячейке центриро вано (!).
Из трех групп ромбической голоэдрии с I-решеткой введением в диагональную позицию символа зеркальной плоскости m, "тянущей" за собой весь спектр плоскостей скользящего отражения - m  n (b n (b  c), или клиноплоскости d получим 3 тетрагональные I-группы 2: c), или клиноплоскости d получим 3 тетрагональные I-группы 2:
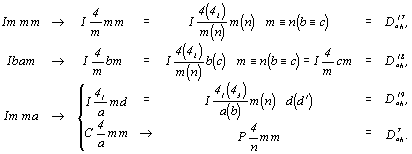
Введение зеркальной плоскости m на третью позицию символа целесообразно лишь в группах, производных от ромбических Immm и Ibam, ибо только в этом случае возникнут поворотные оси 4-го порядка, взаимодействие которых с вектором 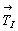 решетки обусловит их чередование с осями 42. Появление результирующей оси 4-го порядка, перпендикулярной к плоскости а при введении диагональной плоскости m в пространственную группу Imma, как было показано выше (см. с. 137), сделает возможным выбор примитивной элементарной ячейки и, следовательно, приведет к уже полученной пространственной группе решетки обусловит их чередование с осями 42. Появление результирующей оси 4-го порядка, перпендикулярной к плоскости а при введении диагональной плоскости m в пространственную группу Imma, как было показано выше (см. с. 137), сделает возможным выбор примитивной элементарной ячейки и, следовательно, приведет к уже полученной пространственной группе 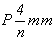 . .
Введение "алмазной" клиноплоскости d на диагональную позицию символа ко всем трем исходным I-группам ромбической голоэдрии лишь в одном случае (Imma) приведет к оригинальной тетрагональной группе 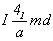 . Ибо только в ней горизонтальная компонента скольжения ( . Ибо только в ней горизонтальная компонента скольжения (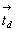 ) диагональной клиноплоскости d , равная ) диагональной клиноплоскости d , равная 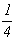 диагонали базисной грани I-ячейки, будет соответствовать одной из компонент, на которые раскладывается вектор диагонали базисной грани I-ячейки, будет соответствовать одной из компонент, на которые раскладывается вектор 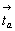 плоскости аz (рис. 85). В результате взаимодействия этих плоскостей (аz . d) возникнут горизонтальные диагональные оси 2-го порядка - поворотные или винтовые, что невозможно в двух других группах (Immm, Ibam), ибо тогда возникли бы оси 2-го порядка с несвойственными им компонентами скольжения в 1/4 и 3/4 диагональной трансляции элементарной ячейки. Кроме того, в результате введения в пр. гр. Immm и Ibam диагональной плоскости d возникли бы винтовые энантиоморфные оси 41 (43), несовместимые с перпендикулярной к ним зер-кальной плоскостью m, так как, будучи в ней отраженными, они станут нейтральными: 4 или 42. плоскости аz (рис. 85). В результате взаимодействия этих плоскостей (аz . d) возникнут горизонтальные диагональные оси 2-го порядка - поворотные или винтовые, что невозможно в двух других группах (Immm, Ibam), ибо тогда возникли бы оси 2-го порядка с несвойственными им компонентами скольжения в 1/4 и 3/4 диагональной трансляции элементарной ячейки. Кроме того, в результате введения в пр. гр. Immm и Ibam диагональной плоскости d возникли бы винтовые энантиоморфные оси 41 (43), несовместимые с перпендикулярной к ним зер-кальной плоскостью m, так как, будучи в ней отраженными, они станут нейтральными: 4 или 42.
Тетрагонализация двух голоэдрических групп с F-решеткой приведет к четырем группам в стандартном для тетрагональной симметрии I-аспекте (см. с. 92). При этом из пр. гр. Fmmm получим уже выведенные ранее объемно-центрированные пр. гр. 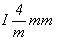 и и 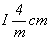 , а из остав-шейся пр. гр. Fddd кроме уже выведенной , а из остав-шейся пр. гр. Fddd кроме уже выведенной 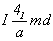 получим оригинальную новую пр. гр. получим оригинальную новую пр. гр. 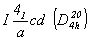 : :
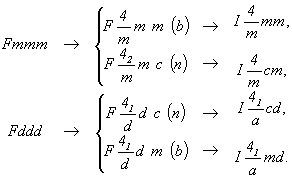
И вновь обращаем внимание на характер производных осей 4-го порядка - 4 (42) или 41 (43) , который будет зависеть от типа порождающих вертикальных плоскостей симметрии (плоскостей 2-й и 3-й позиций символа): 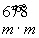 = 4, = 4, 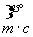 = 42 , = 42 , 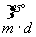 = 41 , = 41 , 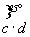 = 43 . Кроме того, характер полученной оси 4-го порядка укажет и на возможный тип перпендикулярной к ней плоскости симметрии (плоскости 1-й позиции символа); ибо нейтральные оси 4 и 42 сочетаются лишь с плоскостями m или n, энантиоморфные оси 41 и 43 сочетаются с перпендикулярными к ним и чередующимися между собой плоскостями a (b). = 43 . Кроме того, характер полученной оси 4-го порядка укажет и на возможный тип перпендикулярной к ней плоскости симметрии (плоскости 1-й позиции символа); ибо нейтральные оси 4 и 42 сочетаются лишь с плоскостями m или n, энантиоморфные оси 41 и 43 сочетаются с перпендикулярными к ним и чередующимися между собой плоскостями a (b).
В итоге, использовав в качестве тетрагонализаторов диагональные плоскости различного типа и добавив их к 20 группам ромбической голоэдрии, получили также 20 тетрагональных голоэдрических групп. Однако, обратившись к схеме вывода точечных групп - 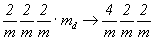 (см. рис. 82), увидим, что этот же результат может быть получен и в том случае, если в роли тетрагонализаторов использовать взаимосвязанные с диагональными плоскостями оси 2-го порядка - 2 или 21. Методически же в качестве порождающих удобно воспользоваться плоскостями симметрии. (см. рис. 82), увидим, что этот же результат может быть получен и в том случае, если в роли тетрагонализаторов использовать взаимосвязанные с диагональными плоскостями оси 2-го порядка - 2 или 21. Методически же в качестве порождающих удобно воспользоваться плоскостями симметрии.
Вывод пространственных групп тетрагональной гемиэдрии на основе ромбических пространственных групп
При переходе к гемиэдрическим пространственным группам тетрагональной сингонии диагональные плоскости md и оси 2-го порядка 2d (тетрагонализаторы) становятся независимыми друг от друга и, будучи введенными в пространственные группы ромбической гемиэдрии классов mm2 и 222, породят пространственные группы, подчиненные разным классам тетрагональной гемиэдрии (см. рис. 82).
Пространственные группы с Р-решеткой
Выписав в качестве исходных подгрупп ромбические гемиморфные пространственные группы с Р-решеткой 3, пригодные для тетрагонализации, т.е. группы с однотипными плоскостями симметрии на первых двух позициях ромбического символа:
Pmm2, Pcc2, Pba2, Pnn2,
Cmm2, Ccc2,
Imm2, Iba2,
Fmm2, Fdd2,
и введя сначала в качестве тетрагонализаторов диагональные плоскости (а таковыми будут m (b) или c (n)), получим 8 тетрагональных групп с Р-решеткой класса 4mm. Задание же на диагональную позицию осей 2-го порядка (на диагональной позиции оси 2 и 21 взаимосвязаны!) приведет еще к четырем пространственным группам класса 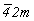 4: 4:
| Ромбические исходные пр. группы |
Ромбические пр. группы в тетрагональном аспекте |
Пространственные группы тетрагональной гемиэдрии |
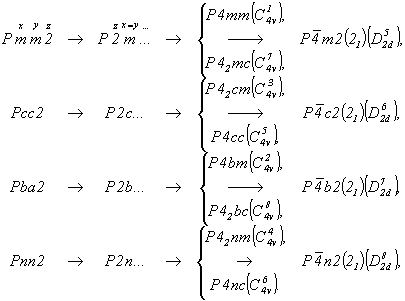 |
Тетрагонализация двух базоцентрированных ромбических групп Cmm2 и Ccc2 с последующим переходом к стандартному Р-аспекту (см. с. 136) приведет либо к уже выведенным Р-группам, подчиненным точечной 4mm (при задании на диагональную позицию возможных на ней плоскостей симметрии), либо к двум группам (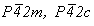 ), подчиненным точечной ), подчиненным точечной 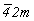 (при задании диагональных осей 2(21)): (при задании диагональных осей 2(21)):
|
Исходные
ромбические
пр. группы
|
Тетрагональные пр. группы |
| в С-аспекте |
в Р-аспекте |
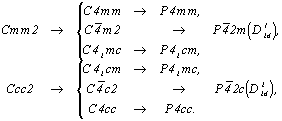 |
Следует еще раз отметить, что, поскольку при переходе от тетрагонального С- к стандартному Р-аспекту координатные и диагональные особые направления меняются местами, плоскости скользящего отражения b и n теряют свои горизонтальные составляющие (в новой Р-ячейке они становятся реальными координатными трансляциями) и приобретают наименования тех плоскостей, с которыми они чередовались в С-ячейке - m и с соответственно. Это приводит к требуемому в Р-решетке чередованию однотипных координатных плоскостей через полтрансляции.
Введение диагональных плоскостей m(b) или c(n) в группы ромбической осевой гемиэдрии:
Р222, Р2221, Р21212, Р212121,
С222, С2221 -
приведет либо к еще не выведенным тетрагональным пространственным группам, подчиненным точечным 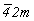 или или 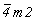 (в случае добавления диагональных плоскостей симметрии), либо к пространственным группам класса 422 (при добавлении диагональных осей 2 (21)): (в случае добавления диагональных плоскостей симметрии), либо к пространственным группам класса 422 (при добавлении диагональных осей 2 (21)):
| Тетрагональные пр. группы |
Исходные ромбические пр. группы |
Тетрагональные пр. группы |
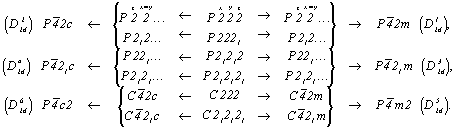 |
Следует отметить, что введение диагональной плоскости m или с в ромбические группы с вертикальной винтовой осью 21 приведет к чередованию горизонтальных координатных осей (2 или 21) через 1/4 трансляции вдоль оси Z, что сократит параметр с элементарной ячейки вдвое и, следовательно, изменит характер вертикальной оси: 21(z) --> 2(z).
При введении в группы ромбической осевой гемиэдрии диагональных осей 2-го порядка следует помнить, что горизонтальные оси могут либо пересекаться, либо скрещиваться. Поэтому необходимо учитывать, с одной стороны, высоту этих осей вдоль оси Z, с другой - их периодичность через полтрансляции вдоль горизонтальных координатных направлений. Вводимая ось при этом не должна размножать исходный осевой комплекс ромбической группы. В результате будем иметь 4 возможных уровня осей 2 (или 21), задаваемых на диагональной позиции: 0, 1/8, 1/4, 3/8 (рис. 86), и соответственно 8 групп тетрагональной осевой гемиэдрии, в которые все 4 ромбические примитивные группы класса 222 будут входить в качестве подгрупп.
Если в исходной ромбической группе вертикальные оси 2-го порядка поворотные, т.е. являются подгруппой осей 4 либо 42 , то диагональные оси следует задавать на высотах 0 или 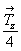 . Если же вертикальная ось винтовая (21), т.е. служит подгруппой осей 41 либо 43 , то высоты диагональных осей будут равны . Если же вертикальная ось винтовая (21), т.е. служит подгруппой осей 41 либо 43 , то высоты диагональных осей будут равны 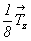 или или 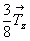 5: 5:
| Исходные ромбические пр. группы |
Ромбические пр. группы в тетрагональном аспекте |
Пространственные группы тетрагональной гемиэдрии |
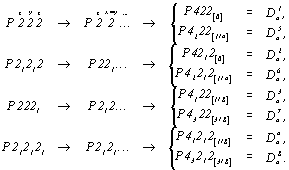 |
Тетрагонализация базоцентрированных ромбических групп С222 и С2221 к новым тетрагональным пространственным группам не приведет:
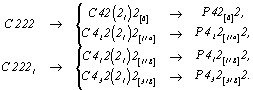
Пространственные группы с I-решеткой
Из двух ромбических гемиморфных пространственных групп с I-решеткой нетрудно получить 6 объемноцентрированных групп тетрагональной гемиэдрии, добавляя плоскости m  n (b v c) или d либо оси симметрии 2(21) на третью позицию символа: n (b v c) или d либо оси симметрии 2(21) на третью позицию символа:
| Исходные ромбические пр. группы |
Ромбические пр. группы в тетрагональном аспекте |
Пространственные группы тетрагональной гемиэдрии |
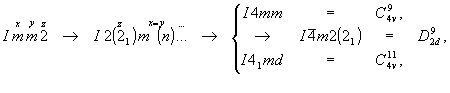 |
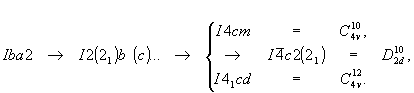 6 6 |
Из двух ромбических групп с F-решеткой (Fmm2 и Fdd2) по этой же схеме могут быть получены две новые тетрагональные группы с I-решеткой (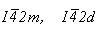 ) помимо четырех уже выведенных на основе ромбических I-групп: ) помимо четырех уже выведенных на основе ромбических I-групп:
| Исходные ромбические пр. группы |
Тетрагональные гемиэдрические группы |
| в F-аспекте |
в I-аспекте |
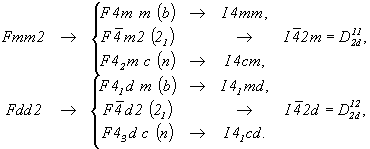 |
Тетрагонализация оставшихся пространственных групп ромбической осевой гемиэдрии с I- и F-решетками приведет лишь к двум новым тетрагональным I-группам - I422 и I4122:
| Исходные ромбические пр. группы |
Пространственные группы тетрагональной гемиэдрии |
| в F- и I-аспекте |
в тетрагональном F- и I-аспекте |
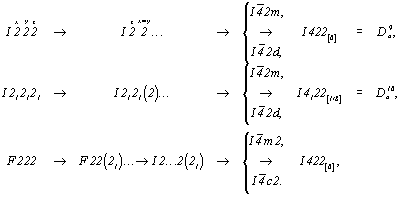 |
Пространственные группы тетрагональной гемиэдрии, подчиненные точечной 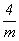 , - группы без горизонтальных особых направлений - удобно вывести непосредственно из голоэдрических групп, как их подгруппы, оставив в символе тетрагональной группы лишь элементы симметрии 1-й позиции. В результате будут получены 4 пространственные группы с Р-решеткой: , - группы без горизонтальных особых направлений - удобно вывести непосредственно из голоэдрических групп, как их подгруппы, оставив в символе тетрагональной группы лишь элементы симметрии 1-й позиции. В результате будут получены 4 пространственные группы с Р-решеткой:
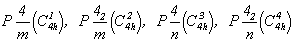
и две пр. гр. с I-решеткой:
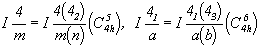 . .
Пространственные группы тетрагональной тетартоэдрии
Вывод пространственных групп тетрагональной тетартоэдрии, по существу, сводится к простому перечислению возможных разновидностей осей 4-го порядка при соответствующих решетках:
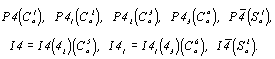
Геологический факультет МГУ
|


