|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Глава II. Точечные группы симметрии
Группы симметрии, oперации которых оставляют хотя бы одну точку пространства на месте, называются точечными группами симметрии. Вывод ограничим кристаллографическими точечными группами, предопределенными симметрией трехмерных периодических построек - решеток (см. с. 74).
32 кристаллографические точечные группы были впервые выведены И.Гесселем в 1830 г. и независимо от него А.В.Гадолиным в 1867 г. Большинство способов вывода основано на переборе допустимых сочетаний порождающих операций симметрии - генераторов групп. Наиболее удобен и нагляден метод перебора на основе анализа геометрического расположения элементов симметрии.
Вывод точечных групп симметрии
Поскольку любая симметрическая операция может быть представлена простым либо инверсионным поворотом (см. с. 7), начать вывод точечных групп симметрии можно с групп, характеризующихся одним из этих элементов симметрии. Процесс вывода состоит в том, чтобы, задавая различные и по-разному ориентированные элементы симметрии относительно исходного, найти конечную кристаллографическую совокупность операций симметрии. При этом возникнут семейства групп, характеризующиеся определенными генераторами и видом связи между ними, т.е. их взаимной ориентацией, а также своей предельной группой симметрии 1. Все кристаллографические группы одного семейства являются подгруппой определенной предельной группы.
1. Группы поворотов Cn - циклические группы 1-го рода , где n - индекс, указывающий на количество операций симметрии группы, приводящих к операции тождества, т.е. n - это порядок самой оси 2, совпадающий с порядком группы.
В случае совмещения осей четного и нечетного порядков появляется результирующая поворотная ось, на порядок которой указывает произведение порядков исходных осей. Например, 3 . 2 = 6. Количество циклических групп соответствует числу возможных кристаллографических осей различного порядка, т.е. n = 1, 2, 3, 4, 6. Предельной для групп поворотов будет группа вращающегося конуса - 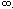 (рис. 17, 1). (рис. 17, 1).
2. Группы инверсионных (зеркальных) поворотов Сni (Sn) - циклические группы 2-го рода - можно разбить на основе порядков осей (n) на 3 семейства: с n = 4k + 4, n = 2k + 1, n = 4k + 2.
Сложные оси симметрии с порядком, кратным четырем (n = 4k + 4), включают в себя мнимые симметрические операции и поэтому не могут быть представлены (заменены) простыми реальными элементами симметрии. При этом порядки инверсионных осей и их зеркальных эквивалентов совпадают. Кристаллографическими оказываются лишь оси 4-го порядка, и так как  = =  , то один и тот же класс симметрии можно обозначить либо С4i ( , то один и тот же класс симметрии можно обозначить либо С4i ( ), либо S4 ( ), либо S4 ( ). ).
Второе семейство сложных осей - осей нечетных порядков (n = 2k + 1) - характеризуется тем, что, казалось бы, мнимые операции, их составляющие, реальны. Например, инверсионная ось 3-го порядка ( ) - это не что иное, как комбинация двух реальных элементов симметрии - поворотной оси 3-го порядка и центра инверсии; зеркальная ось 3-го порядка ( ) - это не что иное, как комбинация двух реальных элементов симметрии - поворотной оси 3-го порядка и центра инверсии; зеркальная ось 3-го порядка (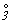 ) - это поворотная ось 3-го порядка и перпендикулярная к ней зеркальная плоскость симметрии, т.е. Cni = Cn . Ci. ) - это поворотная ось 3-го порядка и перпендикулярная к ней зеркальная плоскость симметрии, т.е. Cni = Cn . Ci.
Третье семейство сложных осей - осей четных порядков (n = 4k+2) - характеризуется тем, что они также могут быть заменены реальными (простыми) элементами симметрии. Однако эти элементы симметрии не входят в определение данных осей. Например, инверсионная ось 6-го порядка не содержит ни реального поворота вокруг оси этого же порядка (6), ни центра инверсии. Однако она может быть представлена комбинацией реальных элементов симметрии: оси 3-го порядка и перпендикулярной к ней зеркальной плоскости симметрии, характеризующих ее зеркальный эквивалент. Таким образом,
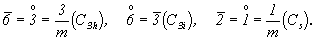
В результате, кроме групп с единственным элементом симметрии (групп Cn и S4), получили группы симметрии, представленные комбинациями элементов симметрии: поворотной оси и расположенного на ней центра инверсии, поворотной оси и перпендикулярной к ней зеркальной плоскости симметрии. Однако если такие комбинации с нечетными осями симметрии являются заменителями соответствующих сложных осей, то добавление центра инверсии или перпендикулярной зеркальной плоскости к четным осям приведет к новым центросимметричным классам Cnh :
C2h = 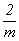 , C4h = , C4h = 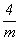 , C6h = , C6h = 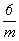 . .
Задание осей 2-го порядка, поворотных или инверсионных, совпадающих с главной осью, поворотной или инверсионной, к новым, еще не выведенным группам симметрии не приведет. Например,
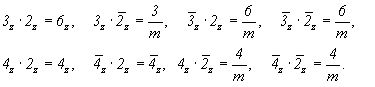
Предельной для всех групп, содержащих зеркальные или инверсионные оси любых порядков в качестве единственного элемента симметрии, а также групп Cnh будет группа вращающегося цилиндра - 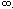 /m (рис. 17,3). /m (рис. 17,3).
3. Группы с осями 2-го порядка, перпендикулярными главной поворотной оси, делятся на два семейства: одно - с побочными поворотными осями 2 (группы Dn), другое - с побочными инверсионными осями 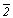 (группы Cnv). (группы Cnv).
Согласно осевой теореме Эйлера ( см. с. 9) два поворота вокруг двух пересекающихся осей могут быть заменены результирующим поворотом вокруг третьей оси. Если исходные оси взаимно перпендикулярны и одна из них - ось 2-го порядка, то результирующей будет еще одна ось 2-го порядка, пересекающаяся с первой под углом  /2, где /2, где  - элементарный угол поворота главной оси. Количество осей 2-го порядка соответствует порядку главной оси. При этом, если главная ось нечетная, то все n побочных осей эквивалентны между собой, т.е. совмещаются друг с другом поворотами на угол - элементарный угол поворота главной оси. Количество осей 2-го порядка соответствует порядку главной оси. При этом, если главная ось нечетная, то все n побочных осей эквивалентны между собой, т.е. совмещаются друг с другом поворотами на угол  вокруг исходной главной оси и располагаются под углом вокруг исходной главной оси и располагаются под углом  /2. Если главная ось четная, то побочные оси разбиваются на два неэквивалентных семейства. Ибо, расположенные относительно друг друга также под углом /2. Если главная ось четная, то побочные оси разбиваются на два неэквивалентных семейства. Ибо, расположенные относительно друг друга также под углом  /2, они не связаны поворотом на этот угол ( /2, они не связаны поворотом на этот угол ( ) вокруг главной оси. Если побочные оси поворотные (2), то получим классы Dn. Например, D3 = 32, но D4 = 422, D6 = 622. В случае же инверсионных осей 2-го порядка ( ) вокруг главной оси. Если побочные оси поворотные (2), то получим классы Dn. Например, D3 = 32, но D4 = 422, D6 = 622. В случае же инверсионных осей 2-го порядка (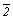 = m = m ) получаем классы Cnv со всеми перечисленными выше особенностями классов Dn ( C3v = 3m, но C4v = 4mm, C6v = 6mm). ) получаем классы Cnv со всеми перечисленными выше особенностями классов Dn ( C3v = 3m, но C4v = 4mm, C6v = 6mm).
Предельной группой для класса Dn будет группа симметрии скрученного цилиндра, два донышка которого вращаются в противоположные стороны, 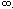 22 (рис. 17, 4), для классов Cnv - группа симметрии неподвижного конуса, 22 (рис. 17, 4), для классов Cnv - группа симметрии неподвижного конуса, 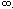 mm (рис. 17, 2). mm (рис. 17, 2).
4. В группах с главной инверсионной осью добавление побочных осей 2-го порядка приводит (на основании теоремы 3, см. с. 19) к появлению побочных инверсионных осей 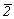 . При этом комбинации с инверсионными осями низших порядков новых классов симметрии не образуют. Например, . При этом комбинации с инверсионными осями низших порядков новых классов симметрии не образуют. Например,
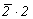  --> --> 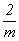 <-- <-- 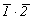  и и 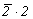  --> mm2 <-- --> mm2 <-- 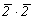  . .
Взаимодействие осей высшего порядка 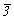 и и 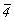 с побочными поворотными осями 2-го порядка приводит к появлению с побочными поворотными осями 2-го порядка приводит к появлению 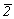 , т.е. побочных плоскостей симметрии, расположенных между побочными осями 2, а следовательно, к классам Dnd . Например, , т.е. побочных плоскостей симметрии, расположенных между побочными осями 2, а следовательно, к классам Dnd . Например,
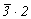  --> --> 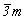 <-- <--   , ,   --> --> 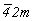 <-- <-- 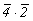  . .
Добавленные к классу  , как и ко всем классам Cnh, побочные оси 2 и , как и ко всем классам Cnh, побочные оси 2 и 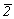 в результате их взаимодействия с горизонтальной плоскостью mz оказываются на пересечении вертикальных и горизонтальной плоскостей симметрии: в результате их взаимодействия с горизонтальной плоскостью mz оказываются на пересечении вертикальных и горизонтальной плоскостей симметрии:
  --> -->  <-- <-- 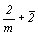  , ,
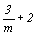  --> --> 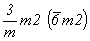 <-- <-- 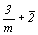  , ,
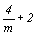  --> --> 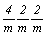 <-- <-- 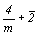  , ,
  --> -->  <-- <-- 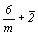  . .
В результате получаем семейство групп Dnh, предельной для которых, так же как и для групп семейства Dnd, будет группа симметрии неподвижного цилиндра  (рис. 17, 5). (рис. 17, 5).
В итоге получено 27 групп симметрии с одним или несколькими единичными направлениями, т.е. направлениями, не повторяющимися какими-либо операциями симметрии данной группы. В таких группах либо нет осей высшего порядка, либо есть только одна.
Группы без единичных направлений - группы с несколькими осями высшего порядка - легко вывести, вновь прибегнув к осевой теореме Эйлера (см. с. 8) и проанализировав величины углов кристаллографического сферического треугольника (см. с. 15) Действительно, учитывая условия существования сферических треугольников, сумма углов которых не должна превышать 540o и не должна быть меньше 180o (180o < А+В+С < 540o , где А, В и С - углы сферического треугольника), приходим лишь к двум комбинациям осей высшего порядка: 3, 3, 2 (60o +60o +90o =210o ) и 4, 3, 2 (45o +60o +90o =195o ).
Зная углы сферических треугольников, по формулам сферической тригонометрии (см. с. 11), можно вычислить и их стороны, т.е. углы между указанными осями симметрии. Для треугольника, образованного выходами двух осей 3-го и одной оси 2-го порядка (3, 3, 2) (рис. 18), сторона 3 - 3 равна 70o 31' 44' ' , сторона 2 - 3 равна 54o 44' 8' ' . Для треугольника 4, 3, 2 сторона 4 - 3 равна 54o 44' 8' ' , сторона 4 - 2 равна 45o и сторона 3 - 2 равна 35o 15' 52' ' (т.е. половине стороны в 70o 31' 44' ' ).
Построив на поверхности сферы рассчитанные сферические треугольники и размножив заданные элементы симметрии (оси) имеющимися симметрическими операциями, получим группы симметрии 1-го рода 23 (Т) и 432 (О), в которых три оси 2-го порядка и три оси 4-го порядка соответственно взаимно перпендикулярны, т. е. могут служить координатными направлениями (рис. 18).
Остальные группы с несколькими осями высшего порядка можно получить, добавляя к уже выведенным исходным осевым группам (23 и 432) операции симметрии 2-го рода: 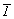 или или 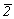 (= m). Добавление инверсии приведет к группам 23 . (= m). Добавление инверсии приведет к группам 23 .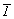 = =  (Тh) и 432 . (Тh) и 432 . 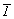 = = = = 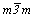 (Oh). При этом, если группа (Oh). При этом, если группа  характеризуется лишь координатными плоскостями симметрии, возникшими за счет взаимодействия центров инверсии с координатными осями 2-го порядка, то в группе характеризуется лишь координатными плоскостями симметрии, возникшими за счет взаимодействия центров инверсии с координатными осями 2-го порядка, то в группе 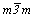 кроме указанных плоскостей появятся и плоскости, перпендикулярные диагональным осям 2-го порядка, - 6 диагональных плоскостей симметрии. Единственно возможным вариантом, не размножающим исходные осевые комплексы и не приводящим к уже выведенным группам, является добавление оси кроме указанных плоскостей появятся и плоскости, перпендикулярные диагональным осям 2-го порядка, - 6 диагональных плоскостей симметрии. Единственно возможным вариантом, не размножающим исходные осевые комплексы и не приводящим к уже выведенным группам, является добавление оси 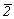 в диагональную позицию группы 23, в результате чего координатные оси 2 повысятся до в диагональную позицию группы 23, в результате чего координатные оси 2 повысятся до 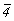 , т.е. возникнет группа , т.е. возникнет группа 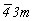 (Td). (Td).
Предельной для групп 23 и 432 будет группа симметрии шара, каждый радиус которого закручен в одну сторону, 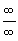 (см. рис. 17, 6), для групп (см. рис. 17, 6), для групп 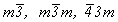 - группа симметрии неподвижного шара - - группа симметрии неподвижного шара - 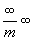 (см. рис. 17, 7). (см. рис. 17, 7).
В итоге выведены 32 точечные кристаллографические группы симметрии с соответствующими им предельными группами. В каждой точечной группе можно выделить минимальную совокупность симметрических операций, порождающих все элементы группы, - генераторы группы, которые могут быть представлены в матричной форме (табл. 2).
Геологический факультет МГУ
|


