|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
I.4. Различные способы представления операций симметрии
Модельный способ иллюстрации операций симметрии наиболее прост и нагляден (см. рис. 1, 3, 4), но позволяет решать лишь конкретные задачи, не выявляя законов взаимодействий симметрических операций в обобщенном виде. Для решения подобной задачи можно прибегнуть к иным способам представления симметрических операций, например к методу координат, основанному на том, что любое симметрическое преобразование может быть представлено с помощью координат исходной и преобразованной точек. Покажем это на конкретных примерах.
Рассмотрим операцию поворота вокруг оси 2-го порядка, совмещенной с осью Z прямоугольной координатной системы (рис. 13). Любая исходная точка с координатами xyz поворотом на 180o вокруг указанной оси 2z будет переведена в положение 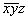 , т.е. неизменной останется координата, соответствующая оси вращения Z, две другие изменят знаки на противоположные. Подмеченная закономерность (для оси 2z - xyz --> , т.е. неизменной останется координата, соответствующая оси вращения Z, две другие изменят знаки на противоположные. Подмеченная закономерность (для оси 2z - xyz --> 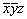 ) ) будет выполняться для любой точки трехмерного пространства в данной системе координат. При изменении ориентации оси вращения эта закономерность сохранится: так, ось 2x, совпадающая с координатной осью X, переведет исходную точку с координатами xyz в положение будет выполняться для любой точки трехмерного пространства в данной системе координат. При изменении ориентации оси вращения эта закономерность сохранится: так, ось 2x, совпадающая с координатной осью X, переведет исходную точку с координатами xyz в положение 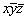 ; ось 2y - xyz --> ; ось 2y - xyz --> 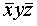 . .
Отражение в плоскости симметрии (my), перпендикулярной оси Y и проходящей через начало координат, преобразует координату исходной точки xyz в 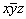 . При этой операции симметрии изменяется лишь знак одной координаты, соответствующей координатной оси, перпендикулярной данной плоскости: для my - xyz --> . При этой операции симметрии изменяется лишь знак одной координаты, соответствующей координатной оси, перпендикулярной данной плоскости: для my - xyz --> 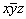 . .
По указанному закону будут изменяться координаты точек, отраженных в плоскостях симметрии разных позиций: mx - xyz --> 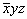 и т.д. и т.д.
Анализ изменения координат точек позволяет решать и обратные задачи: устанавливать связывающие их операции симметрии. Так, нетрудно увидеть, что точки с координатами xyz и 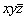 связаны отражением в плоскости, перпендикулярной оси Z (mz), а точки xyz и связаны отражением в плоскости, перпендикулярной оси Z (mz), а точки xyz и 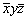 - поворотом вокруг оси 2y. - поворотом вокруг оси 2y.
Методом координат можно решать и конкретные задачи взаимодействия симметрических операций. Так, последовательно проведенные операции отражения в плоскостях mx и my переведут исходную точку с координатами xyz сначала в позицию 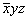 и затем в положение и затем в положение 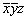 . Координаты точек, исходной и полученной после проведенных преобразований, однозначно указывают на результирующую операцию симметрии - поворот вокруг оси 2z: xyz --> --> . Координаты точек, исходной и полученной после проведенных преобразований, однозначно указывают на результирующую операцию симметрии - поворот вокруг оси 2z: xyz --> --> 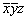 . Операции поворота вокруг оси 2z с последующим отражением в плоскости симметрии mz переведут точку xyz сначала в положение . Операции поворота вокруг оси 2z с последующим отражением в плоскости симметрии mz переведут точку xyz сначала в положение 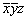 , а затем в , а затем в 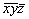 . Анализ координат исходной и результирующей точек указывает на то, что они связаны операцией инверсии: xyz --> --> . Анализ координат исходной и результирующей точек указывает на то, что они связаны операцией инверсии: xyz --> --> 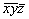 . .
Таким образом, с помощью метода координат мы видим, что взаимодействие оси 2-го порядка с перпендикулярной к ней зеркальной плоскостью симметрии приводит к появлению центра инверсии. Поэтому часто всречающаяся в учебниках запись 4 . m = = 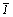 (или 4 . (или 4 . 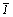 = m = m ) по меньшей мере неверна, ибо противоречит полученному результату. Поворот же на 90o с последующим отражением в m ) по меньшей мере неверна, ибо противоречит полученному результату. Поворот же на 90o с последующим отражением в m соответствует операциям зеркально-поворотной оси соответствует операциям зеркально-поворотной оси 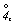 ( xyz --> ( xyz --> 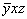 --> --> 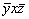 ). Правильной нужно считать запись 42 . m ). Правильной нужно считать запись 42 . m = = 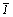 , так же как 63 . m , так же как 63 . m = = 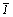 , поскольку 42 = 63 = 2. , поскольку 42 = 63 = 2.
В приведенных примерах операция симметрии рассматривалась как перемещение точек объекта относительно фиксированной координатной системы. Однако тот же результат можно получить путем преобразования (движения) координатной системы относительно неподвижной исходной точки. В этом случае операция симметрии будет представлена преобразованием координатной системы. Нетрудно понять, что операция преобразования координатной системы обратна операции преобразования точек объекта, и наоборот.
Поэтому при описании преобразований симметрии объекта следует различать два аспекта: с одной стороны, симметрия объекта может быть выявлена, если он неподвижен и исследователь меняет систему координат, с другой - объект может быть совмещен сам с собой путем симметрических преобразований при неподвижной координатной системе. Второй подход к операциям симметрии более нагляден, но все же не позволяет, несмотря на тот же конечный результат, сделать обобщения.
Проиллюстрируем сказанное на примере оси 4-го порядка, совмещенной с координатной осью Z, - 4z (рис. 14). Вместо поворота исходной точки 1 с координатами xyz на 90o против часовой стрелки в положение 2 с координатами 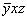 можно преобразовать координатную систему, повернув ее в обратном направлении (по часовой стрелке) на тот же угол вокруг этой же оси 4-го порядка. При таком повороте ось Z останется без изменения, местами и знаками поменяются две другие координатные оси: положение старой оси X займет новая ось Y' , новая же ось X' окажется в положении - Y, т.е. X' = - Y, Y' = X, Z' = Z. При этом масштабные отрезки вдоль координатных осей исходного и преобразованного репера, а также углы между соответствующими осями не изменятся. можно преобразовать координатную систему, повернув ее в обратном направлении (по часовой стрелке) на тот же угол вокруг этой же оси 4-го порядка. При таком повороте ось Z останется без изменения, местами и знаками поменяются две другие координатные оси: положение старой оси X займет новая ось Y' , новая же ось X' окажется в положении - Y, т.е. X' = - Y, Y' = X, Z' = Z. При этом масштабные отрезки вдоль координатных осей исходного и преобразованного репера, а также углы между соответствующими осями не изменятся.
Выразив координаты исходной точки 1 (xyz) в новых преобразованных координатных осях (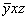 ), легко увидеть, что они не отличаются от координат точки 2, полученной ранее поворотом вокруг оси 4-го порядка. Это же правило будет работать и в том случае, если ось 4-го порядка направить вдоль другой оси, например, вдоль оси Y. Поворот координатной системы вокруг оси 4y оставит без изменения координату y, тогда как координаты x и z поменяются местами и соответственно знаками, т.е. получим точку со следующими координатами: ), легко увидеть, что они не отличаются от координат точки 2, полученной ранее поворотом вокруг оси 4-го порядка. Это же правило будет работать и в том случае, если ось 4-го порядка направить вдоль другой оси, например, вдоль оси Y. Поворот координатной системы вокруг оси 4y оставит без изменения координату y, тогда как координаты x и z поменяются местами и соответственно знаками, т.е. получим точку со следующими координатами: 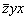 . .
Обобщая все сказанное, представим данное преобразование координатного репера в виде системы уравнений, выразив единичные векторы 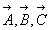 вдоль новых координатных осей как векторные суммы параметров вдоль новых координатных осей как векторные суммы параметров 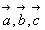 исходной ("старой") координатной системы ( рис. 14): исходной ("старой") координатной системы ( рис. 14):
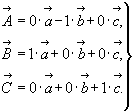
И поскольку характер такого преобразования определяется лишь коэффициентами при единичных векторах 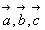 , то систему данных уравнений можно записать сокращенно в виде таблицы, составленной из этих коэффициентов, - матрицы преобразования осей: , то систему данных уравнений можно записать сокращенно в виде таблицы, составленной из этих коэффициентов, - матрицы преобразования осей:
(M)ст--> нов = 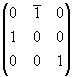 = = 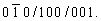
Обратим внимание на то, что при кристаллографических преобразованиях координатных систем - отражениях в зеркальных плоскостях симметрии, поворотах на углы 60, 90, 120 или 180o и инверсии - координатный репер преобразуется сам в себя. Отсюда матрицы соответствующих симметрических преобразований будут иметь своими членами (коэффициентами при единичных векторах) нули и единицы. Это так называемые "ноль, один"-матрицы. И хотя каждая из матриц может быть получена на основании преобразования координатной системы, она отражает соответствующее симметрическое преобразование точек пространства. Составляя такую матрицу, мы фактически отвлекаемся от конкретного геометрического смысла ее членов. Однако следует иметь в виду, что члены матриц преобразования ортогональной координатной системы есть не что иное, как косинусы углов между соответствующими осями новой (преобразованной) и старой (исходной) координатных систем. Поэтому такую матрицу называют матрицей направляющих косинусов.
В общем случае преобразования ортогональных координатных систем, обычно используемых в кристаллофизике, можно выразить системой линейных уравнений:
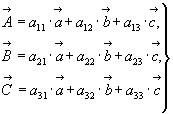 (11) (11)
или соответствующей матрицей:
(M)ст --> нов = 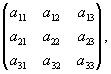
где 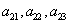 - направляющие косинусы углов между новой осью Y' и старыми осями X, Y, Z; - направляющие косинусы углов между новой осью Y' и старыми осями X, Y, Z; 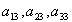 - направляющие косинусы углов между старой осью Z и новыми осями X' , Y' , Z' и т.д. Первый индекс (i) при символе аij относится к новым осям, второй (j) - к старым. Девять коэффициентов aij ( где i,j = 1, 2, 3) зависимы друг от друга, и в общем случае aij - направляющие косинусы углов между старой осью Z и новыми осями X' , Y' , Z' и т.д. Первый индекс (i) при символе аij относится к новым осям, второй (j) - к старым. Девять коэффициентов aij ( где i,j = 1, 2, 3) зависимы друг от друга, и в общем случае aij  aji. aji.
Учитывая вышесказанное, систему уравнений (11) можно представить в следующем виде:
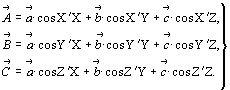
Вернувшись к рассматриваемому примеру с поворотной осью 4-го порядка (см. рис. 14), вычислим единичные векторы преобразованной координатной системы:
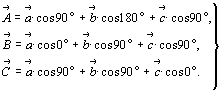
Матрица поворота исходной координатной системы на 90o вокруг оси 4z по часовой стрелке будет иметь тот же вид, что и матрица, составленная на основании векторных сумм (см. с. 22):
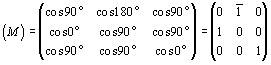 . .
Представление кристаллографических операций симметрии подобными таблицами направляющих косинусов во всех сингониях, как это делается в кристаллофизической практике, удобно лишь в том случае, если и кристаллографическая координатная система ортогональна или она преобразуется в себя при всех операциях группы (моноклинной или триклинной сингоний). Искусственное же введение ортогонального координатного репера в гексагональную сингонию (в присутствии осей 3-го и 6-го порядков) значительно усложняет матрицу направляющих косинусов, тогда как матрица преобразования кристаллографической координатной системы ( a = b  c, c, = =  = 90o , = 90o ,  = 120o , см. с. 41), составленная на основе векторных сумм, будет иметь по сравнению с матрицей ортогонального репера более простой вид. = 120o , см. с. 41), составленная на основе векторных сумм, будет иметь по сравнению с матрицей ортогонального репера более простой вид.
Например, матрица поворота ортогональной координатной системы вокруг оси 3z1 на угол 120o против часовой стрелки имеет следующий вид:
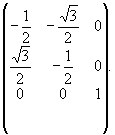
Такую матрицу нельзя использовать непосредственно для расчета символов граней и ребер кристаллов, вычисленных в обычной непрямоугольной кристаллографической координатной системе. Удобнее пользоваться матрицей, составленной на гексагональном кристаллографи-ческом базисе ( = 120o ) (см. с. 41), выразив, как и в предыдущем случае, единичные векторы новой координатной системы как векторные суммы единичных векторов старой системы (рис. 15). Действительно, симметрическое преобразование (поворот вокруг оси 3z1), представленное как преобразование кристаллографической координатной системы в векторной форме, выразится системой уравнений = 120o ) (см. с. 41), выразив, как и в предыдущем случае, единичные векторы новой координатной системы как векторные суммы единичных векторов старой системы (рис. 15). Действительно, симметрическое преобразование (поворот вокруг оси 3z1), представленное как преобразование кристаллографической координатной системы в векторной форме, выразится системой уравнений
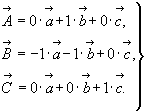
Матрица такого преобразования окажется также "ноль-один"-матрицей:
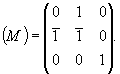
Таким образом, любое симметрическое кристаллографическое преобразование может быть выражено "ноль-один"-матрицей при сохранении во всех случаях кристаллографической координатной системы. И наоборот, любая "0-1"-матрица выражает одну из симметрических операций. При этом, если в триклинной, моноклинной или ортогональных координатных системах "0-1"-матрицы, характеризующие симметрические операции, содержат по одной единице в каждом столбце или строке матрицы, то в гексагональной системе повороты вокруг осей 3-го и 6-го порядков представлены "0-1"-матрицами, содержащими в одной из первых двух строк по две " +1". В результате к 48 различным ортогональным "0-1"-матрицам, описывающим операции симметрии кубической голоэдрии, добавляется 16 (из 24) новых матриц гексагональной голоэдрии [40] (см. с. 42) с двумя "+ 1" в строке. Остальные же 8 преобразований гексагональной голоэдрии записываются ортогональными "0-1"-матрицами (из 48) (табл. 1 ).
Пример. Рассмотрим на матричном языке последовательные действия двух симметрических операций: 2z . mz . Операция поворота вокруг оси 2-го порядка (2z) переводит точку пространства из исходного положения xyz в положение 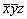 . Отразив вторую точку в горизонтальной плоскости mz , перпендикулярной оси 2, получим точку с координатами . Отразив вторую точку в горизонтальной плоскости mz , перпендикулярной оси 2, получим точку с координатами 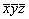 . Зная, что взаимодействие двух операций симметрии приводит к появлению третьей, результирующей, можно ожидать, что и на матричном языке "взаимодействие" двух матриц приведет к новой "0-1"-матрице 1. . Зная, что взаимодействие двух операций симметрии приводит к появлению третьей, результирующей, можно ожидать, что и на матричном языке "взаимодействие" двух матриц приведет к новой "0-1"-матрице 1.
Действительно, каждая из рассматриваемых операций симметрии может быть представлена соответствующей матрицей:
2z - 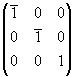 и mz - и mz - 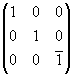 . .
Переход от первой точки к третьей характеризуется результирующей операцией симметрии - инверсией в точке, выраженной соответствующей матрицей 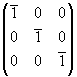 , которую можно получить перемножением исходных матриц. В рассмотренном случае будем иметь , которую можно получить перемножением исходных матриц. В рассмотренном случае будем иметь
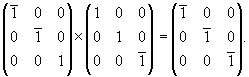
Геологический факультет МГУ
|


